Математические методы исследования экономики.

(системы массового обслуживания)

 

Выполнила: ХХХХХХХХ. Проверил: ХХХХХХ                                                                                    Дата

Студент  групп ХХХХ                                    Оценка:

                            

 

 

Данная работа представляет собой анализ системы массового обслуживания. В ней проводится расчёт основных показателей СМО, которые непосредственно влияют на её работу.

Целью данной расчётно-графической работы является получение теоретических и практических знаний и навыков по анализу систем массового обслуживания (на примере продуктового магазина).

При проведении анализа были использованы элементы теории массового обслуживания, а так же элементы теории вероятностей и математической статистики.

 

 

Визитная карточка организации

 Информация о рассматриваемой системе массового обслуживания (СМО).

 

Наименование организации:

Род деятельности: продуктовый магазин

Место расположения:

Время работы: с 8.00 до 23.00, без обеда и выходных

 

 

Необходимые данные для анализа системы:

 

Рассматриваемый промежуток времени:

Рассматриваемое количество обслуживающих приборов:

2

Рассматриваемые дни:

  дни с понедельника по воскресенье включительно.

Рассматриваемый промежуток времени:

17.00 – 19.00

       (период наибольшей загруженности системы)

 

 

Рассматриваемая единица времени: t = 7,1 минут

 

 

X₁, X₂, …, X_n – число поступивших клиентов в единицу времени.

Y₁, Y₂, …, Y_n – количество обслуженных клиентов в течение единицы времени.

X	Y
10	6
7	4
5	4
8	6
7	5
5	4
6	5
8	6
7	4
5	4
5	4
8	6
4	4
7	6
5	5
9	6
5	4
7	6
8	5
5	5
8	6
5	5
7	5
8	6
6	4
6	4
8	6
7	6
5	5
7	6

 

Проверив данные выборки на подтверждение гипотезы о том, что они из распределения Пуассона, получаем результат: По Х и по У гипотеза подтверждается.

 

 

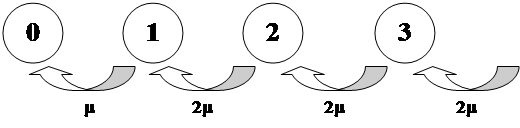
Согласно проверенным выше гипотезам, мы описываем систему массового обслуживания вида:

<М│М│2> (с очередью).

 

где: <М│ - функция распределения промежутка времени между приходами вызовов (т.е. характеристика входного потока);

│М│ - функция распределения времени обслуживания (т.е. характеристика времени обслуживания);

│2> – число приборов в системе;

 (с очередью) – дисциплина обслуживания.

 

 

λ_к = λ

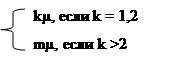μ_к =

λ_к = 6,6

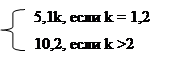μ_к =

 

 

 

 

Проанализируем полученные выборки как выборки из распределения Пуассона.

 

Пусть X(t) – число клиентов в системе в момент t с характеристиками:

 

                                   

 

     

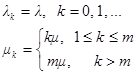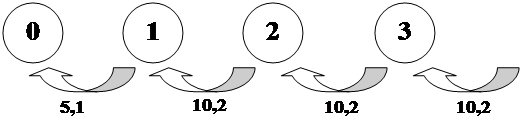
Где λ _k – интенсивность поступления клиентов:

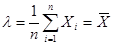 - среднее число клиентов, поступивших в систему, когда система находится в состоянии k в единицу времени.

 

  µ _k – интенсивность обслуживания клиентов:

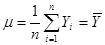 - характеризует среднее число обслуженных клиентов в системе, когда система находится в состоянии k в единицу времени.

 

Следовательно:

 

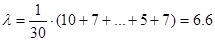 - интенсивность поступления клиентов в систему.

 

 - интенсивность обслуживания клиентов.

Определим основные характеристики системы:

Определим коэффициент загруженности системы :

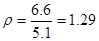 , следовательно, условие стационарности выполняется, так как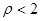

 

В условиях существования стационарного режима

 

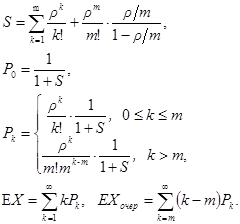
S = 3.3

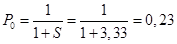 - доля времени простоя

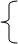          (1.29^k / k!) * 0.23, 0≤ к≤ 2

P_k=   (1.29^k/ 2*2^k-2) * 0.23, к > 2

 

 - вероятность того, что в системе k клиентов

 

Р_з = р^m / (m-1)!(1+S)(m-p) = 1,29²/( 2-1)!(1+3,3)(2-1,29) = 0,545

 

- вероятность, что все приборы заняты

 

 E_q = Р_з / µ( m –p) = 0,545 /5,1*( 2-1,29) = 0,151 единицы времени,

 

 т.е 0,151*7,1 =1,072  минуты в среднем клиент проводит в очереди

 

E_v = E_q +1/µ = 0.151 * 1/5.1 = 0.229 единицы времени.  

т.е. 0,229*7,1 = 1,626 минуты клиент в среднем пребывает в системе

 

E_x = λ* E_v = 6,6*0,229 = 1,51 - среднее число клиентов в системе в единицу времени (7,1 минут).

 

Для того чтобы система массового обслуживания работала эффективно, необходимо, чтобы выполнялись следующие условия:

 

P₀ ≤ 0,1

Для рассматриваемой системы P₀ = 0,23 > 0,1 , это означает, что система работает с чрезмерным простоем и несет тем самым финансовые потери.

Следующее условие, которое должно выполняться:

 

,

 

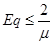То есть должно выполняться: E_q ≤ 0,392, а в нашем случае Eq = 0,151 единицы времени, то есть условие выполняется.

 

Рассчитаем  значение μ, необходимое для снижения времени простоя системы.

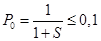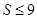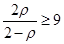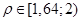; ; ; ; µ ( 3,3; 4,02]

Прежде чем заново рассчитывать характеристики системы, решим неравенство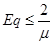

µ ( -оо;4,02][4,02;+оо)

 и посмотрим пересечение интервалов значения 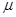, при фиксированном значении 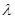. Решением системы неравенств является единственное значение µ=4,02.

Теперь рассчитаем основные характеристики системы при λ = 6,6 и скорректированном значении µ=4,02.

 

р = 6,6/4,02 = 1,64

 

S = 15.1

 

P₀ = 1/1+S = 0.061 доля времени простоя 

 

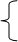          (1.64^k / k!) * 0.061, 0≤ к≤ 2

P_k=   (1.64^k/ 2*2^k-2) * 0.061, к > 2

 

 - вероятность того, что в системе k клиентов

 

Р_з = р^m / (m-1)!(1+S)(m-p) = 1,64²/( 2-1)!(1+15,1)(2-1,64) = 0,46

 

 

- вероятность, что все приборы заняты

 

E_q = Р_з / µ( m –p) = 0,46 /4,02*( 2-1,64) = 0,32 единицы времени

 т.е 0,32*7,1 =2,25  минуты в среднем клиент проводит в очереди

 

E_v = E_q +1/µ = 0.32 * ¼,02 = 0.569 единицы времени.  

 

т.е. 0,569*7,1=4,04 минуты клиент в среднем пребывает в системе

 

E_x = λ* E_v = 6,6*0,569 = 3,75 

 

- среднее число клиентов в системе.

Теперь поставленные условия выполняются:

P₀ ≤ 0,1 ( Р₀ = 0,061)

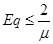 ( E_q =0,32< 2/4,02; E_q = 0,32<0,497

Уменьшение интенсивности обслуживания клиентов приводит к увеличению качества обслуживания клиентов за счет уменьшения доли простоя системы. При времени, проводимом клиентом в очереди – 2.25 минуты это должно привести к привлечению клиентов. Следует учесть, что качество обслуживания влияет на спрос отпускаемой продукции исследуемой системы, что приведет к увеличению прибыли предприятия.

Надо уменьшить интенсивность обслуживания клиентов, что поможет привлечь новых клиентов и получить прибыль.