Математическое описание системы и значения переменных

 

В нашем случае имеем:

При построении математической модели определённого в условии технологического процесса одновременно решается задача оптимизации поверхности отклика 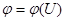, то есть определяются значения факторов, при которых 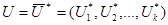, что означает, что 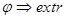. Известно, что одним из наиболее эффективных методов решеня задачи является градиентный метод. Согласно ему в данном случае (исходя из условий задачи) из каждой точки направление движения осуществляется в сторону, противоположную самому градиенту. Отсюда в каждой точке необходимо провести расчет градиента следующего вида:

 

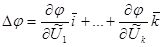, где i и k – единичные орты

 

Как правило, определить всю математическую модель процесса достаточно сложно, поэтому здесь нужно воспользоваться следующей процедурой:

1. В окрестности начальной точки

 

 

 

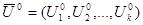
производится полный факторный эксперимент или дробный факторный эксперимент. Мы будем использовать полный факторный эксперимент.

Следует охарактеризовать общие положения проведения полного факторного эксперимента:

Применение полного факторного эксперимента позволяет найти оптимальное расположение точек в факторном пространстве и осуществить линейное преобразование координат, благодаря чему обеспечивается возможность преодолеть недостатки классического регрессионного анализа, в частности корреляцию между коэффициентами уравнения регрессии.

Некоторые обозначения для дальнейшего понимания изложения материала:

Xj-факторы;

Рj- регрессионные коэффициенты системы;

Y- выходная переменная (функция отклика);

М [f]- математическое ожидание помехи;

D [f] – дисперсия помехи;

l – число уровней ;

k – количество факторов;

Уровень факторов – граница исследования области по данному параметру;

Точка с координатами (Х₀(1), Х₀(2), …) - центр плана, или основной уровень;

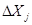- единица варьирования, или интервал варьирования;

S – дисперсия;

вектор В - вектор коэффициентов регрессии;

N - число опытов в матрице планирования;

Р - коэффициент взаимодействия;

b_j - несмешанные оценки;

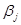 - генеральные коэффициенты;

S2_воспр - дисперсия воспроизводимости;

t_j - критерий Стьюдента;

F – критерий Фишера.

Выбор плана исследования эксперимента определяется постановкой задачи исследования и особенностями объекта. Пусть имеем математическую модель системы:

 

 

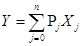
Также нам известны характер помехи и статистические параметры: М[f] = 0 и D[f] = 0,8. Необходимо отметить, что под помехами понимают ряд факторов, искажающих результаты опыта. Если существуют определённые априорные сведения об источнике помех, то можно построить оптимальные планы исследования, учитывающие их влияние, и повысить таким образом точность анализа результата.

В данной задаче требуется провести полный факторный эксперимент.

Полный факторный эксперимент, или метод планирования эксперимента позволяет свести к минимуму число необходимых опытов и одновременно получить оптимальные значения искомых функций. При планировании эксперимента, условия опыта представляют собой фиксированное число значений для каждого фактора. Полный факторный эксперимент фактически представляет собой применение классических метода наименьших квадратов и регрессионного анализа, проводимых по определённому плану.

Процесс исследования обычно разбивается на отдельные этапы. Информация, полученная после каждого этапа, определяет дальнейшую стратегию эксперимента. Таким образом возникает возможность оптимального управления экспериментом. Планирование эксперимента позволяет одновременно варьировать все факторы и получать количественные оценки основных эффектов и эффектов взаимодействия.

Интересующие исследователя эффекты определяются со значительно меньшей ошибкой, чем та, которая характерна для других методов исследования.

В конечном счете, применение методов планирования эксперимента значительно повышает эффективность эксперимента.

Так как при планировании по схеме полного факторного эксперимента реализуются все возможные комбинации факторов на всех выбранных для исследования уровнях, то необходимое число опытов N при полном факторном эксперименте определяется по формуле: N=l^k.

Если эксперименты проводятся только на двух уровнях при двух значениях факторов и при этом в процессе эксперимента осуществляются все возможные комбинации из k факторов, то такой план носит название полный факторный эксперимент типа 2^k.

Описание алгоритма моделирования сводится к следующему:

1. Определяется для любого фактора:

 

Х_{0 j} = (Х _{j max} + Х _{j min} ) / 2,

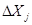 = (Х_jmax - Х_jmin) / 2, j = 1,2,…..k ;

2. От основной системы координат (Х₁, Х₂ , …Х_n ) переходим к безразмерной системе координат (U₁, U₂ , …U_n ) c помощью формулы перехода:

 

U_j = (Х _j - Х _j⁰ ) / 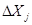, j = 1,2,…..k;

 

В безразмерной системе координат верхний уровень равен +1, а нижний равен –1, координаты центра плана равны нулю и совпадают с началом координат.

3. План эксперимента:

В матрицу планирования (Табл. 1.1) записываются все возможные значения граничных величин в натуральном масштабе.

Таблица 1.1

Номер опыта	Значения факторов в натуральном масштабе				выход
	X1	X2	…	Xn	Y
1	X11	X 12	…	X 1 n	Y1
2	X 21	X2 2	…	X 2 n	Y2
….	…	…	…	…	...
N	X N1	X N2	…	XNn	YN

 

4. Введём фиктивный столбец U₀ в матрицу и запишем матрицу в безразмерной форме (Табл.1.2):

 

Таблица 1.2

Номер опыта	фиктивный столбец	Значения факторов в безразмерной системе координат				Выход
	U0	U1	U2	…	Un	У
1	+1	+1	+1	…	+1	У1
2	+1	-1	+1	…	+1	У2
...	…	…	…	…	….	…
N	+1	-1	-1	…	-1	УN

 

5. Приведём полную матрицу планирования (Табл. 1.3.):

 

Таблица 1.3

Номер опыта	Значения факторов									Выход
	В натуральном масштабе				В безразмерной системе координат
	X1	X2	…	Xn	U 0	U1	U2	…	Un	Y
1	X11	X12	…	X1n	+1	+1	+1	…	+1	Y1
2	X21	X22	…	X2n	+1	-1	+1	…	+1	Y2
…	…	…	…	…	…	…	…	…	…	…
N	XN1	X N2	…	XNn	+1	-1	-1	…	-1	YN

 

Предложенный план эксперимента обладает следующими свойствами:

Свойство симметричности.

 

;

 

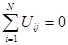Свойство нормировки.

 

;

 

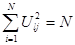Свойство ортогональности.

 

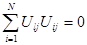, ( l 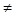j , l,i = 1…k );

 

Следует отметить, что ортогональные планы полный факторный эксперимент ( для линейных моделей ) обладают также рототабельностью. Последнее предполагает равенство и минимальность дисперсий предсказанных значений выходной переменной для всех точек факторного пространства. По закону накопления ошибок для дисперсии предсказанных уравнением регрессии значений выходной переменной можно записать:

 

s²_y= s²_b0 + s²_b1U₁² + … + s²_bnU_n²

Дисперсии коэффициентов регрессии равны между собою, поэтому

 

s²_y = s²_bi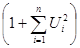

 

С учетом того, что

 

,

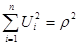Где 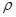 - радиус сферы имеем

 

s²_y = s² _bi .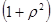

 

Отсюда ясно, что дисперсия предсказанного значения выходной переменной зависит только от радиуса сферы. Это свойство рототабельности эквивалентно независимости дисперсии выходной переменной от вращения координат в центре плана и оправдано при поиске оптимума градиентными методами. Интуитивно понятно, что исследователю удобно иметь дело с такой информацией, содержащейся в уравнении регрессии, которая равномерно «размазана» по сфере радиусом 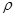. Действительно такое положение можно признать разумным, ибо с помощью уравнения регрессии будут предприниматься попытки предсказать положение ещё неизвестных участков факторного пространства. Равноценность этих участков в смысле ошибки предсказания, по-видимому, является необходимой.

Свойство ортогональности существенно облегчает процесс вычисления коэффициентов, так как корреляционная матрица (U^ТU)^-1 становится диагональной, и коэффициенты будут равны 1/N;

6. С учетом свойства ортогональности можно вычислить вектор В коэффициентов регрессии:

 

 

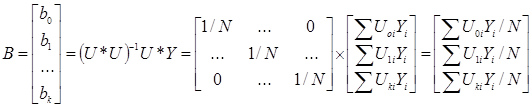
Следовательно, любой коэффициент уравнения регрессии bj определяется скалярным произведением столбца Y на соответствующий столбец Uj, деленным на число опытов N в матрице планирования:

 

 

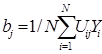
Вычислим коэффициенты регрессии линейного уравнения :

 

 

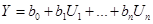
Если в рассмотрение ввести более полное уравнение регрессии с коэффициентами взаимодействия Р, то используя процедуру метода наименьших квадратов , получим:

 

.

 

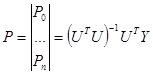Пользуясь планом, представленным в табл. 1.2, можно перечислить коэффициенты регрессии и записать в табл.1.4:

 

Y = Р₀ + Р₁U₁ + Р₂U₂ + … + Р_nU_n + … +

+…+ P₁₃U₁U₃ + P₂₃U₂U₃ + … + P₁₂₃U₁U₂U₃…

 

Таблица 1.4

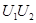
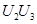
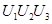
Номер опыта	U0	U1	U2	…	Un	…				…	У
1	+1	+1	+1	…	+1	…	-1	+1	+1	…	У1
2	+1	-1	+1	…	+1	…	-1	-1	+1	…	У2
…	…	…	…	…	…	…	…	…	…	…	…
N	+1	-1	-1	…	-1	…	-1	+1	+1	…	УN

 

P₁₂, P₂₃ - эффекты двойного взаимодействия, а P₁₂₃ - эффекты тройного взаимодействия. Эффекты взаимодействия определяют аналогично линейным эффектам:

.

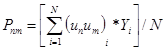7. Проверка однородности дисперсии и значимости коэффициентов регрессии.

Если дополнительно поставить параллельные опыты, можно определить s²_воспр - дисперсию воспроизводимости, проверить значимость коэффициентов регрессии, а при наличии степеней свободы – адекватность уравнения.

В связи с тем, что корреляционная матрица (U*U)^-1 для спланированного эксперимента есть матрица диагональная

 

,

 

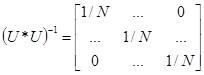коэффициенты уравнения регрессии некоррелированы между собой. Значимость коэффициентов уравнения регрессии можно проверять для каждого коэффициента в отдельности, пользуясь критерием Стьюдента : 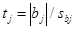. Исключение из уравнения регрессии незначимого коэффициента не скажется на значениях остальных коэффициентов. При этом выборочные коэффициенты b_j оказываются так называемыми несмешанными оценками для соответствующих генеральных коэффициентов β_j:

b_j 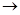β_j, т. е. величины коэффициентов уравнения регрессии характеризуют вклад каждого фактора в величину y.

Диагональные элементы корреляционной матрицы равны между собой, поэтому все коэффициенты уравнений

 

Y = 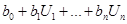 и Y = Р₀ + Р₁U₁ + Р₂U₂ + … + Р_nU_n + … +

+ … +  

 

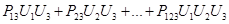
oпределяются с одинаковой точностью:

 

s _bj= s²_воспр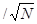

8. Проверка адекватности уравнения

Проверка адекватности уравнения проводится по критерию Фишера:

Рассчитывается значение

 

F= s²_ост/ s²_воспр ; s²_{ост ,}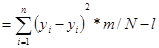

 

где m - число значимых коэффициентов в уравнении регрессии.

2. После проведения полного факторного эксперимента определены коэффициенты регрессии

 

 

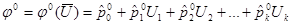
Тогда частные производные будут пропорциональны .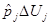

3. Делая, с учетом последнего выражения, шаг в сторону, противоположную среднему, определяем новую точку 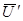 и опять проводим эксперимент.

4. Повторяем первые три шага, пока не приблизимся к точке экстремума. При приближении к точке экстремума алгоритм начинает работать плохо при близости к нулю частных производных, то есть линейная модель становится неадекватной и требует введения квадратичных членов.

По условию дано:

 

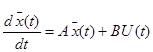
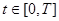, T = 20, U(t) = 15 – 0.1t, .

 

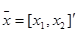Уравнение выхода системы:

 

, , .

 

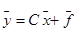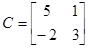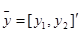Значение параметров системы:

 

, .

 

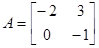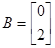Характер помехи и ее статистические параметры:

Нормальное распределение

 

.

 

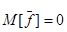Здесь 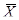- вектор состояния системы; 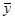- вектор наблюдения; 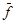- вектор помехи; А, В, С – матрицы коэффициентов (параметров) системы; [0, T] – интервал определения системы.

Необходимо

- составить в соответствии с математическим ожиданием системы ее имитационную модель для формирования реализации вектора и состояния системы на интервале определения;

- составить алгоритм и программу решения задачи построения динамической модели в соответствии с заданным типом модели методом идентификации и точностью решения задачи;

- отладить программу;

- провести расчеты и анализ полученных результатов.