 |
Главная |
Нахождение показателей Ляпунова для особых точек. Определение характера особых точек.
|
из
5.00
|
1) точка O (0,0). Положим в уравнениях (2.3) и (2.4) 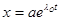 ,
,  и приравняем левые части к нулю.
и приравняем левые части к нулю.
В итоге получим:
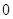 =
=  , (2.8)
, (2.8)
 (2.9)
(2.9)
где проведем линеаризацию, т.е. опустим все нелинейные слагаемые по малым смещениям 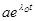 и
и 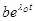 . В результате получим
. В результате получим
 (2.10)
(2.10)
 (2.11)
(2.11)
Условие разрешимости системы имеет вид:
 ,
,
D = 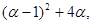 (2.12)
(2.12)
 =
=  .
.
Таким образом видимо, что корни рациональны и имеют разные знаки. Следовательно точка О является седлом.
2) Точка  . Положим в уравнениях (2.3) и (2.4)
. Положим в уравнениях (2.3) и (2.4)  ,
,  и приравняем левые части к нулю.
и приравняем левые части к нулю.
В итоге получим:
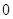 =
=  , (2.13)
, (2.13)
 (2.14)
(2.14)
где проведем линеаризацию, т.е. опустим все нелинейные слагаемые по малым смещениям  и
и 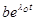 . В результате получим
. В результате получим
 (2.15)
(2.15)
 (2.16)
(2.16)
В итоге ляпуновские показатели для точки S будут следующими:
 =
= 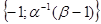 . (2.17)
. (2.17)
Таким образом видно, что корни также рациональны и имеют разные знаки. Следовательно, точка S является седлом.
2) Точка 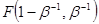 . Положим в уравнениях (2.3) и (2.4)
. Положим в уравнениях (2.3) и (2.4)  ,
,  и приравняем левые части к нулю.
и приравняем левые части к нулю.
В итоге получим:
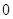 =
=  , (2.18)
, (2.18)
 (2.19)
(2.19)
где проведем линеаризацию, т.е. опустим все нелинейные слагаемые по малым смещениям  и
и 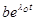 . В результате получим
. В результате получим
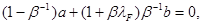 (2.20)
(2.20)
 (2.21)
(2.21)
В итоге ляпуновские показатели для точки S будут следующими:
 =
=  . (2.22)
. (2.22)
Проведем анализ полученных результатов. С учетом того, что в формуле (2.22) присутствует радикал то можно сделать вывод, что при значениях параметра  , ограниченных сверху величиной
, ограниченных сверху величиной
 =
=  , (2.23)
, (2.23)
ляпуновские показатели вещественны и отрицательны а с ростом до значений превышающих критическое, они становятся комплексными с отрицательной действительной частью. Следовательно, в этих пределах точка F представляет устойчивые узел и фокус соответственно.
Можно сделать вывод, что системы, в которых предпочтителен колебательный режим реализуются, если интенсивность процессов аннигиляции жертвы мала по сравнению с интенсивностью процесса ее поглощения хищником. С другой стороны, характерное время автономной эволюции хищника должно быть малым в сравнении с соответствующим временем для жертвы.
Построение фазовых портретов
Для построения фазовых портретов были использованы слабый численный метод Рунге-Кутта 4 порядка точности. Среда реализации – математический пакет Matlab. Для получения данных, численно интегрировалась обезразмеренная система дифференциальных уравнений (2.3), (2.4). Полученные результаты изображены на рис. 2.1-2.2.
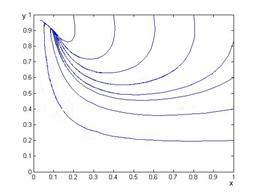
Рисунок 2.1. — Фазовый портрет системы «Хищник-жертва»: режим регрессии. 
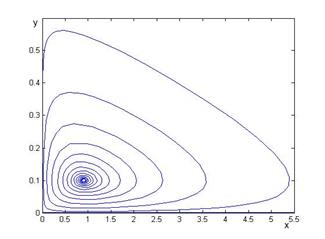
Рисунок 2.2. — Фазовый портрет системы «Хищник-жертва»: режим регрессии. 
Волны пластической деформации
Постановка задачи
Необходимо получить уравнение с безразмерными величинами, определить координаты особых точек. Найти показатели Ляпунова для особых точек, определить характер их устойчивости. Построить фазовые портреты системы.
|
из
5.00
|
Обсуждение в статье: Нахождение показателей Ляпунова для особых точек. Определение характера особых точек. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

