Оценки средних значений

 

Оценка математического ожидания случайных величин X вычисляется по формуле:

 

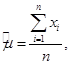
(3.1)

 

где n – количество элементов.

Для случайных величин 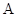 и 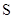 она равна:

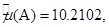
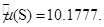
Оценка дисперсии случайных величин вычисляется по формуле:

 

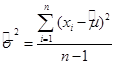.                                (3.2)

 

Для случайных величин 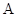 и 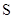она равна:

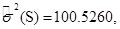
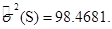
Оценка корреляции случайных величин вычисляется по формулам:

 

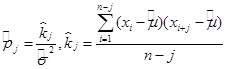,          (3.3)

 

где j = 1,…,n.

Графики корреляции показаны на рисунках 3.1. и 3.2.

 

 

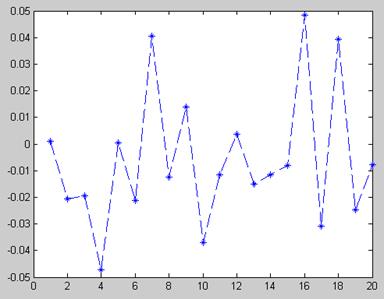
Рисунок 3.1 – Корреляция величины

 

 

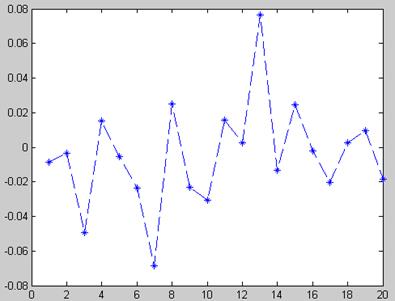
Рисунок 3.2 – Корреляция величины S

 

Графики зависимости последующего значения от предыдущего представлены на рисунках 3.3 и 3.4.

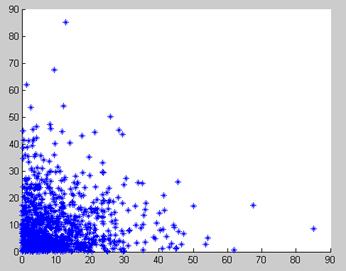
Рисунок 3.3 – Зависимость 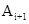 от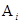

 

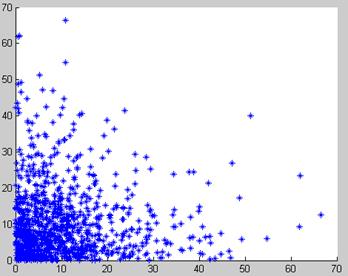
Рисунок 3.4 – Зависимость 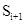 от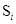

 

Интервальные оценки

 

Доверительный интервал для оценки математического ожидания случайной величины определяется формулой:

 

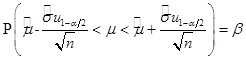, (3.4)

где b = 0.95 – доверительная вероятность, 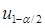 - квантиль порядка 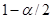,  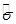=  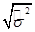- оценка дисперсии.  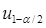= 1.96 для доверительной вероятности 0.95.

Доверительные интервалы для оценки математического ожидания случайных величин 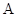 и 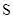 равны:

(9.5886; 10.8315), 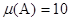– попадает в полученный доверительный интервал;

(9.5627; 10.7928), 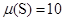– попадает в полученный доверительный интервал.

 

Проверка статистических гипотез

 

Проверка гипотез об экспоненциальном распределении величин A и S осуществляется с помощью метода c².

Выдвигаем гипотезу о том, что случайные величины A и S распределены экспоненциально.

Статистическая функция вычисляется по формуле:

 

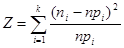 , (3.5)

 

где 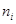- это частота попадания в k –й интервал, p_i - вероятность попадания, которая вычисляется следующим образом

 

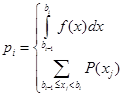,  (3.6)

 

Расчет проводился на k = 20. Если 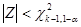, то гипотеза принимается, если 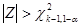, гипотеза отвергается. По данным таблицы для k=20 и 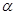=0.05, критерий c² = 31.4.

В результате были получены следующие значения 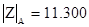 и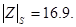

Таким образом, обе гипотезы принимаются.

Интервалы: [0 0,4879), [0.4879 1.0008), [1.0008 1.5415), [1.5415 2.1131), [2.1131 2.7193), [2.7193 3.3647), [3.3647 4.0547), [4.0547 4.7957), [4.7957 5.5962), [5.5962 6.4663), [6.4663 7.4194), [7.4194 8.4730), [8.4730 9.6508), [9.6508 10.9861), [10.9861 12.5276), [12.5276 14.3508), [14.3508 16.5823), [16.5823 19.4591), [19.4591 23.5138) .

 

Метод гистограмм

 

На рисунках 3.5 и 3.6 изображены гистограммы с функциями плотностей распределения вероятностей для A и S.

 

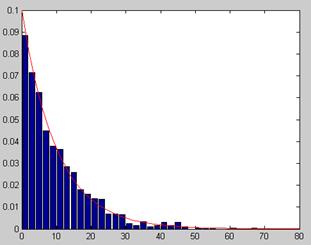
Рисунок 3.5 –Гистограмма величины A

 

Эта гистограмма показывает, что смоделированная случайная величина A распределена по экспоненциальному закону. Математическое ожидание случайной величины А равно 10.

 

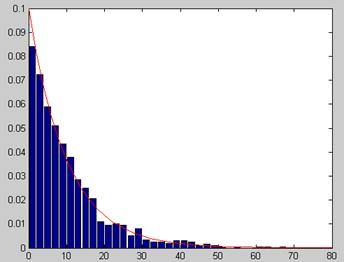
Рисунок 3.6 –Гистограмма величины S

 

На гистограмме видно, что смоделированная случайная величина S распределена по экспоненциальному закону. Математическое ожидание случайной величины S равно 10.

На рисунках 3.7 и 3.8 изображены графики функций распределения вероятностей для A и S.

 

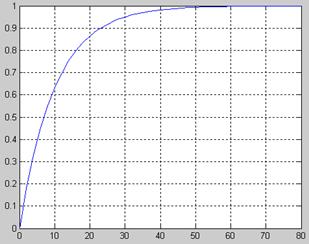
Рисунок 3.7 – Функция распределения величины A

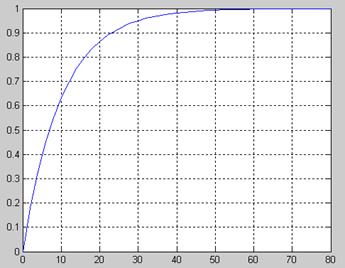
Рисунок 3.8 – Функция распределения величины S

Логика работы программы