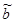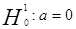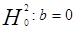|
Главная |
Критерий согласия (критерий Пирсона).
|
из
5.00
|
Как бы хорошо ни была подобрана теоретическая кривая, между нею и статистическим распределением неизбежны некоторые расхождения. Для выяснения их пользуются «критериями согласия». Одним из наиболее применяемых- является так называемый «критерий 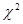 » Пирсона.
» Пирсона.
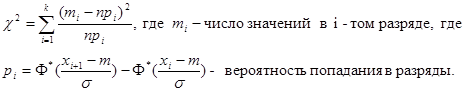
Расчетная часть.
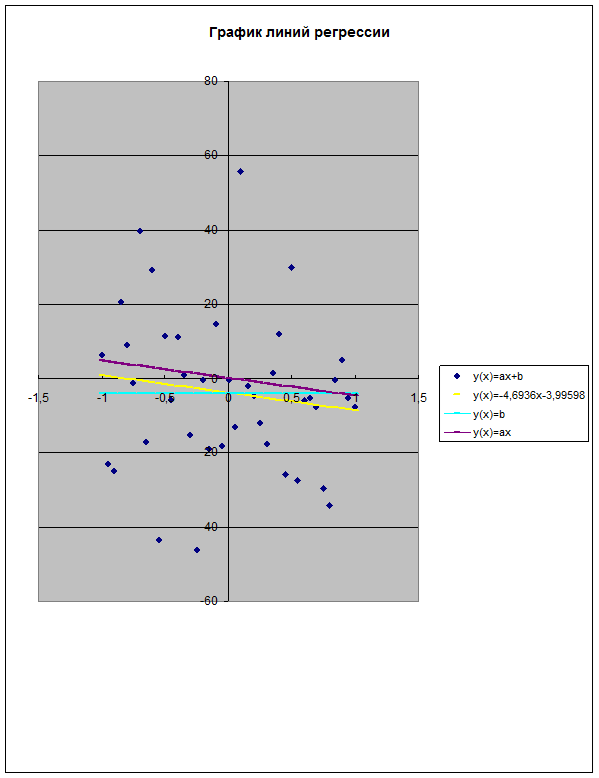
1.Построение оценок 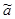 и
и 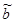 неизвестных коэффициентов.
неизвестных коэффициентов.
Суть метода наименьших квадратов состоит в том, что 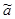 и
и 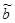 находятся из условия минимума функции S(a,b):
находятся из условия минимума функции S(a,b):
S(a,b)= 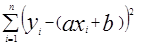 , где n=41.
, где n=41.
| № п / п | X i | Y i | X 2 | XY |  xi+ xi+ 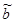
| 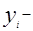 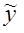
| 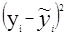
|
| 1 | -1 | 6,323 | 1 | -6,323 | 0,697624 | 5,625376 | 31,64486 |
| 2 | -0,95 | -22,817 | 0,9025 | 21,67615 | 0,462944 | -23,2799 | 541,9558 |
| 3 | -0,9 | -24,908 | 0,81 | 22,4172 | 0,228264 | -25,1363 | 631,8318 |
| 4 | -0,85 | 20,708 | 0,7225 | -17,6018 | -0,00642 | 20,71442 | 429,087 |
| 5 | -0,8 | 9,145 | 0,64 | -7,316 | -0,2411 | 9,386096 | 88,0988 |
| 6 | -0,75 | -1,283 | 0,5625 | 0,96225 | -0,47578 | -0,80722 | 0,65161 |
| 7 | -0,7 | 39,694 | 0,49 | -27,7858 | -0,71046 | 40,40446 | 1632,52 |
| 8 | -0,65 | -16,954 | 0,4225 | 11,0201 | -0,94514 | -16,0089 | 256,2837 |
| 9 | -0,6 | 29,198 | 0,36 | -17,5188 | -1,17982 | 30,37782 | 922,8117 |
| 10 | -0,55 | -43,22 | 0,3025 | 23,771 | -1,4145 | -41,8055 | 1747,7 |
| 11 | -0,5 | 11,371 | 0,25 | -5,6855 | -1,64918 | 13,02018 | 169,525 |
| 12 | -0,45 | -5,745 | 0,2025 | 2,58525 | -1,88386 | -3,86114 | 14,90843 |
| 13 | -0,4 | 11,171 | 0,16 | -4,4684 | -2,11854 | 13,28954 | 176,6118 |
| 14 | -0,35 | 1,058 | 0,1225 | -0,3703 | -2,35322 | 3,411216 | 11,63639 |
| 15 | -0,3 | -15,19 | 0,09 | 4,557 | -2,5879 | -12,6021 | 158,813 |
| 16 | -0,25 | -45,976 | 0,0625 | 11,494 | -2,82258 | -43,1534 | 1862,218 |
| 17 | -0,2 | -0,25 | 0,04 | 0,05 | -3,05726 | 2,807256 | 7,880685 |
| 18 | -0,15 | -18,76 | 0,0225 | 2,814 | -3,29194 | -15,4681 | 239,261 |
| 19 | -0,1 | 14,7 | 0,01 | -1,47 | -3,52662 | 18,22662 | 332,2095 |
| 20 | -0,05 | -17,959 | 0,0025 | 0,89795 | -3,7613 | -14,1977 | 201,5748 |
| 21 | 0 | -0,377 | 0 | 0 | -3,99598 | 3,618976 | 13,09698 |
| 22 | 0,05 | -12,988 | 0,0025 | -0,6494 | -4,23066 | -8,75734 | 76,69108 |
| 23 | 0,1 | 55,728 | 0,01 | 5,5728 | -4,46534 | 60,19334 | 3623,238 |
| 24 | 0,15 | -2,009 | 0,0225 | -0,30135 | -4,70002 | 2,691016 | 7,241564 |
| 25 | 0,2 | -4,523 | 0,04 | -0,9046 | -4,9347 | 0,411695 | 0,169493 |
| 26 | 0,25 | -11,937 | 0,0625 | -2,98425 | -5,16938 | -6,76762 | 45,80074 |
| 27 | 0,3 | -17,419 | 0,09 | -5,2257 | -5,40406 | -12,0149 | 144,3589 |
| 28 | 0,35 | 1,564 | 0,1225 | 0,5474 | -5,63874 | 7,202735 | 51,8794 |
| 29 | 0,4 | 12 | 0,16 | 4,8 | -5,87342 | 17,87342 | 319,459 |
| 30 | 0,45 | -25,92 | 0,2025 | -11,664 | -6,1081 | -19,8119 | 392,5116 |
| 31 | 0,5 | 29,946 | 0,25 | 14,973 | -6,34278 | 36,28878 | 1316,875 |
| 32 | 0,55 | -27,554 | 0,3025 | -15,1547 | -6,57746 | -20,9765 | 440,0154 |
| 33 | 0,6 | -6,12 | 0,36 | -3,672 | -6,81214 | 0,692135 | 0,479051 |
| 34 | 0,65 | -5,25 | 0,4225 | -3,4125 | -7,04682 | 1,796815 | 3,228545 |
| 35 | 0,7 | -7,488 | 0,49 | -5,2416 | -7,2815 | -0,2065 | 0,042644 |
| 36 | 0,75 | -29,674 | 0,5625 | -22,2555 | -7,51618 | -22,1578 | 490,9692 |
| 37 | 0,8 | -34,196 | 0,64 | -27,3568 | -7,75086 | -26,4451 | 699,3457 |
| 38 | 0,85 | -0,239 | 0,7225 | -0,20315 | -7,98554 | 7,746535 | 60,0088 |
| 39 | 0,9 | 4,966 | 0,81 | 4,4694 | -8,22021 | 13,18621 | 173,8763 |
| 40 | 0,95 | -5,11 | 0,9025 | -4,8545 | -8,45489 | 3,344895 | 11,18832 |
| 41 | 1 | -7,541 | 1 | -7,541 | -8,68957 | 1,148575 | 1,319224 |
| Результаты | 0 | -163,835 |
14,35
-67,3532
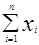
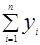
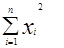
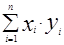
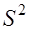


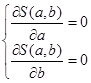 , решив эту систему, найдем
, решив эту систему, найдем 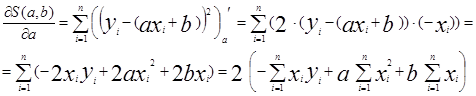
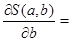
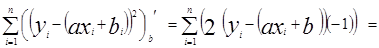
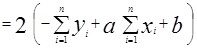
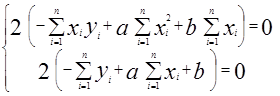
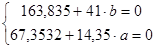
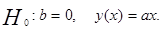
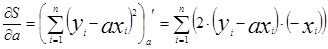
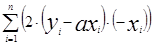 =0
=0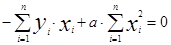
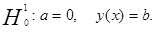
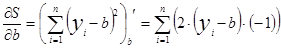
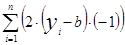 =0
=0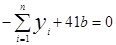
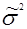 неизвестной дисперсии σ2 шумов εt .
неизвестной дисперсии σ2 шумов εt .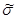 2=
2= 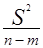 , где S2=(y-ỹ)T*( y-ỹ), n=41(число измерений), m=2(количество неизвестных параметров).
, где S2=(y-ỹ)T*( y-ỹ), n=41(число измерений), m=2(количество неизвестных параметров).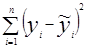 , где
, где 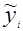 - оценка кривой регрессии,
- оценка кривой регрессии, 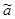 xi+
xi+ 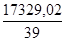 =444,334
=444,334
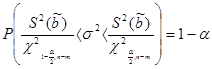 ,
,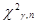 - квантиль уровня
- квантиль уровня 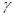 для
для 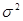 :
: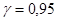 ,
, 
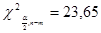
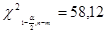
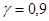 ,
, 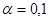
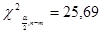
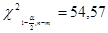
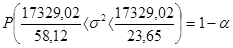 ,
,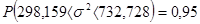 .
.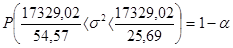
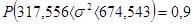
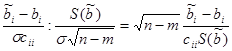 ~t(n-m),
~t(n-m), ,
,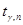 - квантиль уровня
- квантиль уровня 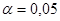
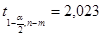
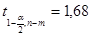
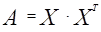 ,
,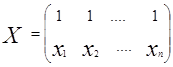 ,
,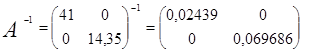
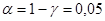 ,
,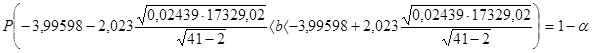
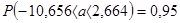
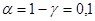 ,
,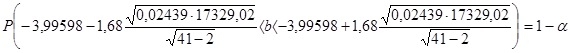
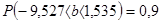 .
.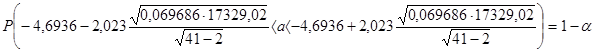
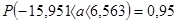
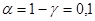 ,
,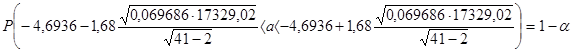
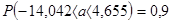
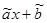
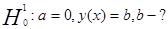
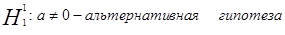 ,
,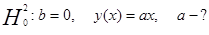
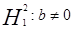
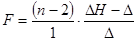 , где
, где 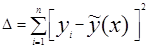
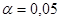
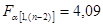
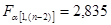
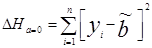 = 17645,1476
= 17645,1476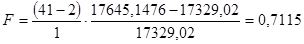
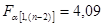 , поэтому принимаем гипотезу
, поэтому принимаем гипотезу 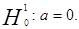
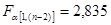 , поэтому принимаем гипотезу
, поэтому принимаем гипотезу 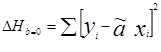 = 17983,7
= 17983,7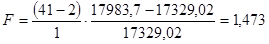
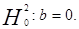
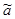 и
и 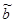 .
.