 |
Главная |
Простейшая теорема вложения
|
из
5.00
|
Теорема 1.  вложено в
вложено в 
Доказательство. Пусть  непрерывно дифференцируема на отрезке
непрерывно дифференцируема на отрезке  Согласно теореме о среднем, вследствие непрерывности
Согласно теореме о среднем, вследствие непрерывности 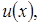 найдётся точка
найдётся точка 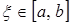 такая, что
такая, что  Поэтому на отрезке
Поэтому на отрезке 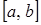 справедливо следующее тождество:
справедливо следующее тождество:
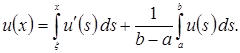
С помощью неравенства Коши-Буняковского имеем

где  Следовательно, для любой непрерывно дифференцируемой на отрезке
Следовательно, для любой непрерывно дифференцируемой на отрезке 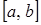 функции
функции  справедливо неравенство
справедливо неравенство
 (1.8)
(1.8)
Пусть теперь последовательность  – фундаментальная по норме
– фундаментальная по норме  Тогда
Тогда

при  Следовательно,
Следовательно,  фундаментальна в смысле равномерной сходимости и, по критерию Коши равномерной сходимости, сходится к
фундаментальна в смысле равномерной сходимости и, по критерию Коши равномерной сходимости, сходится к  Тем более
Тем более  в среднем. Таким образом, в классе из
в среднем. Таким образом, в классе из  содержащим
содержащим  в качестве представителя, содержится непрерывная функция
в качестве представителя, содержится непрерывная функция  и, значит, этот класс можно отождествить с
и, значит, этот класс можно отождествить с  Отождествим элементы
Отождествим элементы  с непрерывными функциями. Пусть
с непрерывными функциями. Пусть  Переходя в неравенстве
Переходя в неравенстве  к пределу при
к пределу при  придём к неравенству (1.8).
придём к неравенству (1.8).
Итак, вложение  в
в  доказано. Доказательство теоремы закончено.
доказано. Доказательство теоремы закончено.
1.5 Пространства Соболева  и
и 
Пусть  – односвязная область с достаточно гладкой границей
– односвязная область с достаточно гладкой границей  В замкнутой области
В замкнутой области  рассмотрим линейное пространство всевозможных непрерывно дифференцируемых функций
рассмотрим линейное пространство всевозможных непрерывно дифференцируемых функций  со скалярным произведением
со скалярным произведением

При этом
 (1.9)
(1.9)
Полученное пространство со скалярным произведением обозначается  а его пополнение – это, по определению, пространство Соболева
а его пополнение – это, по определению, пространство Соболева 
Пусть  – фундаментальная последовательность в
– фундаментальная последовательность в 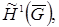 то есть
то есть  при
при  Отсюда следует, что в
Отсюда следует, что в  будут фундаментальными последовательности
будут фундаментальными последовательности

Вследствие полноты  в
в  имеются элементы, которые мы обозначим
имеются элементы, которые мы обозначим

так что при  в среднем
в среднем

Элементы  называются обобщёнными частными производными элемента
называются обобщёнными частными производными элемента 
Скалярное произведение и норма задаются в  теми же формулами, что и в
теми же формулами, что и в  в которых теперь производные обобщённые, а интегрирование понимается в смысле Лебега. Введем в рассмотрение пространство
в которых теперь производные обобщённые, а интегрирование понимается в смысле Лебега. Введем в рассмотрение пространство  Это пространство является пополнением в норме
Это пространство является пополнением в норме
 (1.10)
(1.10)
линейного пространства функций, непрерывно дифференцируемых на 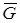 и таких, что
и таких, что 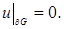
 является гильбертовым пространством со скалярным произведением
является гильбертовым пространством со скалярным произведением

Лемма 3. Если  а
а 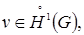 то
то



Доказательство. Достаточно доказать первую из этих формул. Она справедлива, если  а
а  Пусть
Пусть  – фундаментальная в
– фундаментальная в  последовательность, предел которой – элемент
последовательность, предел которой – элемент  Переходя в тождестве
Переходя в тождестве  к пределу при
к пределу при  получим для любой
получим для любой  Действительно, из сходимости в
Действительно, из сходимости в  следует, что
следует, что
 то есть непрерывность скалярного произведения.
то есть непрерывность скалярного произведения.
Пусть теперь 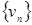 – фундаментальная последовательность в
– фундаментальная последовательность в  Перейдём к пределу в тождестве
Перейдём к пределу в тождестве  и получим исходное тождество.
и получим исходное тождество.
Следствие.  содержится строго внутри
содержится строго внутри 
Действительно, функция  Но
Но  иначе мы имели бы
иначе мы имели бы  то есть
то есть 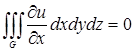 для любой
для любой  Возьмём
Возьмём  и получим противоречие.
и получим противоречие.
Теорема 2 (Фридрихс). Существует постоянная  такая, что для любых
такая, что для любых 

Доказательство. По самому определению  всякий элемент из
всякий элемент из  принадлежит
принадлежит 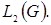 Пусть
Пусть  и сходится в
и сходится в  к
к 
Построим куб  содержащий область
содержащий область  Функции
Функции  доопределим нулём в
доопределим нулём в  Частная производная
Частная производная  существует всюду в
существует всюду в  за исключением, быть может, тех точек, в которых прямая, параллельная оси абсцисс, пересекает границу
за исключением, быть может, тех точек, в которых прямая, параллельная оси абсцисс, пересекает границу  области
области  Для любой точки
Для любой точки  имеем
имеем

По неравенству Коши-Буняковского

Интегрируя полученное неравенство по  находим
находим

Так как  вне
вне  то
то

Переходя к пределу при  приходим к доказываемому неравенству Фридрихса.
приходим к доказываемому неравенству Фридрихса.
Следствие 1. Пространство  вложено в
вложено в 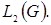
Это предложение непосредственно вытекает из определения вложения банаховых пространств и неравенства Фридрихса.
Следствие 2. В  нормы (1.9) и (1.10) эквивалентны.
нормы (1.9) и (1.10) эквивалентны.
Действительно, используя неравенство Фридрихса, имеем

|
из
5.00
|
Обсуждение в статье: Простейшая теорема вложения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

