Методика изучения площадей фигур в курсе геометрии средней школы

В теме «Площади фигур» наблюдается синтез традиционно-синтетического и аналитического методов. Изучаемые здесь факты носят аналитический характер (например площадь треугольника), а доказательства основаны на применении традиционно-синтетического метода.

При изучении темы «Площади фигур» используется такая схема:

простая фигура – площадь фигуры как величина – площадь прямоугольника – площадь параллелограмма – площадь трапеции – площадь подобных фигур.

Перед введением понятия «простые фигуры» учащимся предлагается по готовым чертежам назвать: простую ломаную, замкнутую ломаную, простую замкнутую ломаную, выпуклый многоугольник, плоский треугольник, плоский пятиугольник. Напомним, что из определения треугольника как фигуры состоящей из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки следует, что он должен представляться как «скелет», «каркас»! Плоский треугольник – конечная часть плоскости, ограниченная треугольником. Выпуклый многоугольник – многоугольник, который лежит в одной плоскости относительно любой прямой, содержащей его сторону. Плоским многоугольником называется конечная часть плоскости, ограниченная многоугольником. Простая замкнутая ломаная называется многоугольником. После этого дается определение:

Геометрическую фигуру будем называть простой, если ее можно разбить на конечное число плоских треугольников. Примером простой фигуры может служить плоский выпуклый многоугольник, который разбивается на плоские треугольники диагоналями, выходящими из одной вершины.

«Площадь простой фигуры – это положительная величина, численное значение которой обладает следующими свойствами:

1) равные фигуры имеют равные площади;

2) если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей ее частей;

3) площадь квадрата со стороной, равной единице измерения, равна единице;

В таком определении новой величины использован аксиоматический подход. С помощью свойств описана аддитивность площади простой фигуры, определена мера (единица измерения) площади. Первое свойство площади определяет термин «равновеликие». Если фигуры равны, то равны и их площади, однако обратное утверждение не всегда верно.

С формулами площадей некоторых фигур учащиеся познакомились в курсе арифметики. Измеряя площади при помощи памятки, школьники познакомились с оценкой ее по недостатку и по избытку. И таким образом они уже подготовлены к восприятию вывода формулы площади прямоугольника.

Первоначально доказываем следующее свойство: площади двух прямоугольников с равными основаниями относятся как их высоты.

а) Прямоугольники ABCD и AB1C1D имеют равное основание AD. Пусть S и S1 – их площади. Разобьем сторону АВ на n равных частей, длина одной части равна  . Пусть m – число точек деления, лежащих на стороне АВ1. Тогда:  ≤

Разделив это неравенство почленно на АВ, получим:

б) Проводим через точки деления прямые, параллельные АD. Получим n равных треугольников со сторонами АD и , площади которых (по св-ву 1) равны и принимают значение  . Поэтому, площадь АВСD выражается неравенством:

.

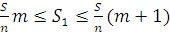Разделив почленно на S, получаем:

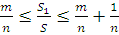
в) Отношение  и  удовлетворяют одним и тем же неравенствам, причем числа  и  отличаются на величину  .При сколь угодно больших n значение  становится очень малым, а это возможно только тогда, когда числа равны. Итак:

		1		1				в

Для вывода формулы площади прямоугольника воспользуемся только что доказанным свойством по отношению к квадрату, со стороной 1 и прямоугольником со сторонами 1 и а и а и в. Получаем:

= ;  => S1=а, S=S1 в.

Следовательно:

S=ав.

Площади подобных фигур.

Площади подобных фигур относятся как квадраты их соответствующих линейных размеров.

При доказательстве этого утверждения используют понятие простой фигуры, определение подобных фигур. Если фигура 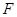 разбивается на простые треугольники, площади которых обозначим через , а фигура - на треугольники, площади которых  и фигуры и  подобны с коэффициентом , то линейные размеры треугольников  в  раз изменены, по отношению к размерам треугольников , то: и т. д., поэтому:

Площадь круга.

Круг – плоская фигура, но ее нельзя разбить на простые треугольники. Поэтому, такая фигура имеет площадь S, если существуют содержащие её простые фигуры и содержащиеся в ней простые фигуры с площадями, как угодно мало отличающимися от S.

При проведении уроков по теме «Площадь фигур» вывод общих формул должен закрепляться на частных примерах. Изложение теоретического материала должно быть максимально сокращено (в разумных пределах), что позволило бы сэкономить время для решения более сложных задач. (Возможно проведение уроков-лекций для изложения теории). Желательно проводить самостоятельные работы, как обучающего, так и контролирующего характера по каждому из изучаемых случаев.