 |
Главная |
Перечень условных обозначений
|
из
5.00
|
Содержание
Перечень условных обозначений
Введение
Описание конечных групп с плотной системой 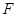 -субнормальных подгрупп для формации
-субнормальных подгрупп для формации 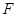 сверхразрешимых групп
сверхразрешимых групп
Заключение
Литература
Перечень условных обозначений
В работе все рассматриваемые группы предполагаются конечными. Используются обозначения, принятые в книгах. Буквами 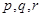 обозначаются простые числа.
обозначаются простые числа.
Будем различать знак включения множеств 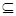 и знак строгого включения
и знак строгого включения 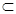 ;
;
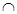 и
и 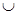 --- соответственно знаки пересечения и объединения множеств;
--- соответственно знаки пересечения и объединения множеств;
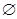 --- пустое множество;
--- пустое множество;
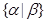 --- множество всех
--- множество всех 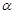 , для которых выполняется условие
, для которых выполняется условие 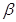 ;
;
 --- множество всех простых чисел;
--- множество всех простых чисел;
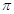 --- некоторое множество простых чисел, т.е.
--- некоторое множество простых чисел, т.е. 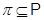 ;
;
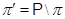 --- дополнение к
--- дополнение к 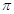 во множестве всех простых чисел; в частности,
во множестве всех простых чисел; в частности, 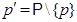 ;
;
примарное число --- любое число вида 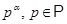 ;
;
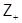 --- множество всех целых положительных чисел.
--- множество всех целых положительных чисел.
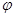 --- некоторое линейное упорядочение множества всех простых чисел
--- некоторое линейное упорядочение множества всех простых чисел 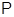 .
.
Запись 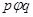 означает, что
означает, что 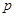 предшествует
предшествует 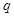 в упорядочении
в упорядочении 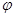 ,
, 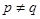 .
.
Пусть  --- группа. Тогда:
--- группа. Тогда:
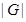 --- порядок группы
--- порядок группы  ;
;
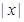 --- порядок элемента
--- порядок элемента 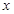 группы
группы  ;
;
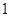 --- единичный элемент и единичная подгруппа группы
--- единичный элемент и единичная подгруппа группы  ;
;
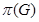 --- множество всех простых делителей порядка группы
--- множество всех простых делителей порядка группы  ;
;
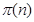 --- множество всех различных простых делителей натурального числа
--- множество всех различных простых делителей натурального числа 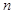 ;
;
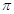 --группа --- группа
--группа --- группа  , для которой
, для которой 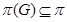 ;
;
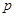 --группа --- группа
--группа --- группа  , для которой
, для которой 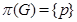 ;
;
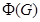 --- подгруппа Фраттини группы
--- подгруппа Фраттини группы  , т.е. пересечение всех максимальных подгрупп группы
, т.е. пересечение всех максимальных подгрупп группы  ;
;
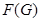 --- подгруппа Фиттинга группы
--- подгруппа Фиттинга группы  , т.е. произведение всех нормальных нильпотентных подгрупп группы
, т.е. произведение всех нормальных нильпотентных подгрупп группы  ;
;
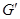 --- коммутант группы
--- коммутант группы  ;
;
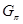 ---
--- 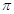 --холловская подгруппа группы
--холловская подгруппа группы  ;
;
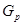 --- силовская
--- силовская 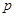 --подгруппа группы
--подгруппа группы  ;
;
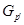 --- дополнение к силовской
--- дополнение к силовской 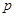 --подгруппе в группе
--подгруппе в группе  , т.е.
, т.е. 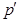 --холловская подгруппа группы
--холловская подгруппа группы  ;
;
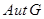 --- группа всех автоморфизмов группы
--- группа всех автоморфизмов группы  ;
;
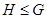 ---
--- 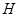 является подгруппой группы
является подгруппой группы  ;
;
нетривиальная подгруппа --- неединичная собственная подгруппа;
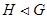 ---
--- 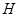 является нормальной подгруппой группы
является нормальной подгруппой группы  ;
;
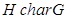 --- подгруппа
--- подгруппа 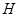 характеристична в группе
характеристична в группе  , т.е.
, т.е. 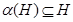 для любого автоморфизма
для любого автоморфизма 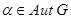 ;
;
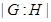 --- индекс подгруппы
--- индекс подгруппы 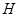 в группе
в группе  ;
;
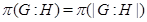 ;
;
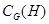 --- централизатор подгруппы
--- централизатор подгруппы 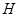 в группе
в группе  ;
;
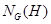 --- нормализатор подгруппы
--- нормализатор подгруппы 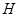 в группе
в группе  ;
;
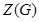 --- центр группы
--- центр группы  ;
;
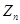 --- циклическая группа порядка
--- циклическая группа порядка 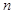 ;
;
Если 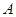 и
и 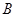 --- подгруппы группы
--- подгруппы группы  , то:
, то:
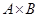 --- прямое произведение подгрупп
--- прямое произведение подгрупп 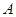 и
и 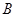 ;
;
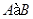 --- полупрямое произведение нормальной подгруппы
--- полупрямое произведение нормальной подгруппы 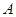 и подгруппы
и подгруппы 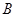 .
.
Группа  называется:
называется:
примарной, если 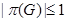 ;
;
бипримарной, если 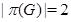 .
.
Скобки  применяются для обозначения подгрупп, порождённых некоторым множеством элементов или подгрупп.
применяются для обозначения подгрупп, порождённых некоторым множеством элементов или подгрупп.
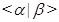 --- подгруппа, порожденная всеми
--- подгруппа, порожденная всеми 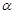 , для которых выполняется
, для которых выполняется 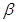 .
.
Группу  называют
называют 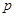 --нильпотентной, если
--нильпотентной, если 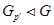 .
.
Группу  порядка
порядка 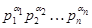 называют
называют 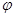 --дисперсивной, если выполняется
--дисперсивной, если выполняется 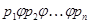 и для любого
и для любого 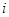
 имеет нормальную подгруппу порядка
имеет нормальную подгруппу порядка 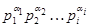 . Если при этом упорядочение
. Если при этом упорядочение 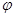 таково, что
таково, что 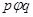 всегда влечет
всегда влечет 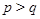 , то
, то 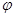 --дисперсивная группа называется дисперсивной по Оре.
--дисперсивная группа называется дисперсивной по Оре.
Цепь --- это совокупность вложенных друг в друга подгрупп. Ряд подгрупп --- это цепь, состоящая из конечного числа членов и проходящая через единицу. Цепь 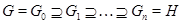 называется
называется 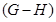 -цепью (с индексами
-цепью (с индексами 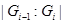 ); если при этом
); если при этом 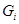 является максимальной подгруппой в
является максимальной подгруппой в 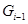 для любого
для любого 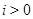 , то указанная цепь называется максимальной
, то указанная цепь называется максимальной 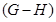 -цепью.
-цепью.
Ряд подгрупп 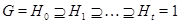 называется:
называется:
субнормальным, если 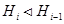 для любого
для любого 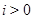 ;
;
нормальным, если 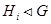 для любого
для любого 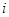 .
.
Нормальный ряд называется главным, если 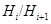 является минимальной нормальной подгруппой в
является минимальной нормальной подгруппой в 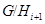 для всех
для всех 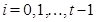 .
.
Классы групп, т.е. совокупности групп, замкнутые относительно изоморфизмов, обозначаются прописными готическими буквами. Так же обозначаются формации, т.е. классы групп, замкнутые относительно факторгрупп и подпрямых произведений. За некоторыми классами закреплены стандартные обозначения:
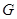 --- класс всех групп;
--- класс всех групп;
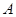 --- класс всех абелевых групп;
--- класс всех абелевых групп;
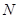 --- класс всех нильпотентных групп;
--- класс всех нильпотентных групп;
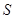 --- класс всех разрешимых групп;
--- класс всех разрешимых групп;
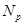 --- класс всех
--- класс всех 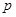 --групп;
--групп;
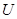 --- класс всех сверхразрешимых групп.
--- класс всех сверхразрешимых групп.
Пусть  --- некоторый класс групп и
--- некоторый класс групп и 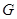 --- группа, тогда:
--- группа, тогда:
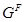 ---
---  --корадикал группы
--корадикал группы 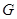 , т.е. пересечение всех тех нормальных подгрупп
, т.е. пересечение всех тех нормальных подгрупп 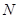 из
из 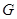 , для которых
, для которых 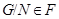 . Если
. Если  --- формация, то
--- формация, то 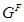 является наименьшей нормальной подгруппой группы
является наименьшей нормальной подгруппой группы 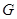 , факторгруппа по которой принадлежит
, факторгруппа по которой принадлежит 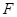 . Если
. Если 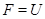 --- формация всех сверхразрешимых групп, то
--- формация всех сверхразрешимых групп, то 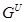 называется сверхразрешимым корадикалом группы
называется сверхразрешимым корадикалом группы 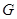 .
.
Формация  называется насыщенной, если всегда из
называется насыщенной, если всегда из 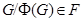 следует, что и
следует, что и 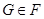 . Класс групп
. Класс групп 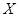 называется наследственным или
называется наследственным или 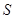 -замкнутым, если из того, что
-замкнутым, если из того, что 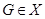 , следует, что и каждая подгруппа группы
, следует, что и каждая подгруппа группы 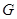 также принадлежит
также принадлежит 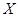 .
.
Пусть  --- некоторая непустая формация. Максимальная подгруппа
--- некоторая непустая формация. Максимальная подгруппа 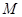 группы
группы 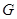 называется:
называется:
 -нормальной, если
-нормальной, если 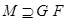 ;
;
 -абнормальной, если
-абнормальной, если 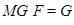 .
.
Максимальная 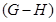 -цепь
-цепь 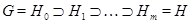 называется
называется 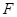 -субнормальной, если для любого
-субнормальной, если для любого 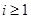 подгруппа
подгруппа 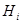
 -нормальна в
-нормальна в 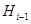 . Подгруппа
. Подгруппа 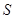 группы
группы 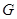 называется
называется  -субнормальной, если существует хотя бы одна
-субнормальной, если существует хотя бы одна 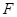 -субнормальная максимальная
-субнормальная максимальная 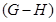 -цепь.
-цепь.
Группа 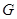 называется группой с плотной системой
называется группой с плотной системой  -субнормальных подгрупп, если для любых двух различных подгрупп
-субнормальных подгрупп, если для любых двух различных подгрупп 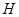 и
и 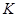 группы
группы 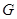 , из которых первая содержится во второй и не максимальна в ней, в группе
, из которых первая содержится во второй и не максимальна в ней, в группе 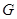 существует такая
существует такая 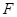 -субнормальная подгруппа
-субнормальная подгруппа 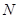 , что
, что 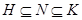 . В этом случае также говорят, что множество
. В этом случае также говорят, что множество  -субнормальных в
-субнормальных в 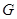 подгрупп плотно.
подгрупп плотно.
Введение
Изучение строения групп по заданным свойствам системы их подгрупп является одним из основных направлений в теории конечных групп. Отметим, что темп и глубина таких исследований непрерывно возрастают. Это направление изучения групп берет свое начало с групп Миллера-Морено, групп Шмидта. В качестве свойств, налагаемых на системы подгрупп, рассматривались абелевость, нормальность, субнормальность, дополняемость и др. Это направление получило широкое развитие в работах многих ведущих алгебраистов.
С дедекиндовых групп, то есть групп, у которых нормальны все подгруппы, началось изучение различных (как конечных, так и бесконечных) групп, у которых некоторая система подгрупп 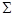 удовлетворяет условию нормальности. Описание конечных дедекиндовых групп дано в работе Р. Дедекинда, а бесконечных в работе Р. Бэра. Эти работы определили важное направление исследований в теории групп. Главной целью этого направления является описание обобщенно дедекиндовых групп. Эти обобщения дедекиндовых групп осуществляются либо путем сужения системы подгрупп
удовлетворяет условию нормальности. Описание конечных дедекиндовых групп дано в работе Р. Дедекинда, а бесконечных в работе Р. Бэра. Эти работы определили важное направление исследований в теории групп. Главной целью этого направления является описание обобщенно дедекиндовых групп. Эти обобщения дедекиндовых групп осуществляются либо путем сужения системы подгрупп 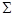 , то есть подгрупп нормальных во всей группе, либо ослабления свойства нормальности для подгрупп из
, то есть подгрупп нормальных во всей группе, либо ослабления свойства нормальности для подгрупп из 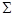 . Среди таких обобщений выделим следующие исследования.
. Среди таких обобщений выделим следующие исследования.
Первое существенное обобщение дедекиндовых групп принадлежит О.Ю. Шмидту. Он описал конечные группы с одним и двумя классами сопряженных ненормальных подгрупп, а также установил нильпотентность конечной группы, у которой нормальны все максимальные подгруппы. Конечные группы с нормальными 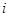 -тыми максимальными подгруппами изучали Б. Хупперт и З. Янко. Д.Бакли изучал конечные группы, у которых нормальны все минимальные подгруппы.
-тыми максимальными подгруппами изучали Б. Хупперт и З. Янко. Д.Бакли изучал конечные группы, у которых нормальны все минимальные подгруппы.
Значительные расширения класса дедекиндовых групп возникают при переходе от условия нормальности к различным ее обобщениям, как, например, к квазинормальности, субнормальности, нормализаторным условиям и др.
В начале 70-х годов по инициативе С.Н.Черникова началось изучение групп с плотными системами подгрупп. Система подгрупп группы 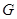 , обладающая некоторым свойством
, обладающая некоторым свойством 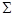 , называется плотной в
, называется плотной в 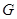 , если для любых двух подгрупп
, если для любых двух подгрупп 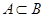 из
из 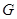 , где
, где 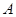 не максимальна в
не максимальна в 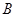 , найдется
, найдется 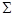 -подгруппа
-подгруппа 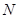 такая, что
такая, что 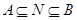 . Группы с плотной системой дополняемых подгрупп были изучены С.Н.Черниковым.
. Группы с плотной системой дополняемых подгрупп были изучены С.Н.Черниковым.
В 1974 году С.Н.Черников поставил следующий вопрос: каково строение группы 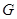 , в которой множество всех ее субнормальных подгрупп плотно? Ответ на этот вопрос был получен А.Манном и В.В.Пылаевым.
, в которой множество всех ее субнормальных подгрупп плотно? Ответ на этот вопрос был получен А.Манном и В.В.Пылаевым.
Заметим, что в теории формаций понятие субнормальности обобщается следующим образом. Говорят, что подгруппа 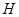 является
является 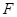 -субнормальной в
-субнормальной в 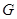 , если существует цепь подгрупп
, если существует цепь подгрупп
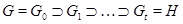
такая, что 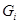 является
является  -нормальной максимальной подгруппой в
-нормальной максимальной подгруппой в 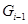 для любого
для любого 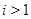 . Если
. Если  совпадает с классом всех нильпотентных групп (который является, конечно,
совпадает с классом всех нильпотентных групп (который является, конечно, 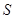 -замкнутой насыщенной формацией), то
-замкнутой насыщенной формацией), то 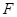 -субнормальная подгруппа оказывается субнормальной.
-субнормальная подгруппа оказывается субнормальной.
В связи с развитием теории формаций большое внимание стало уделяться исследованию конечных групп, насыщенных  --подгруппами,
--подгруппами, 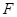 --субнормальными или
--субнормальными или  --абнормальными подгруппами. В этом направлении проводили свои исследования Л.А.Шеметков, Гашюц, Картер, Шмид, Хоукс и другие.
--абнормальными подгруппами. В этом направлении проводили свои исследования Л.А.Шеметков, Гашюц, Картер, Шмид, Хоукс и другие.
Ясно, что вопрос С.Н.Черникова можно сформулировать в следующей общей форме: если  ---
--- 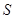 -замкнутая насыщенная формация, то каково строение группы, в которой множество всех ее
-замкнутая насыщенная формация, то каково строение группы, в которой множество всех ее  -субнормальных подгрупп плотно?
-субнормальных подгрупп плотно?
В таком виде вопрос С.Н.Черникова был исследован в работе для случая, когда  --- класс всех
--- класс всех 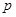 -нильпотентных групп. В настоящей работе мы исследуем данный вопрос в случаях, когда
-нильпотентных групп. В настоящей работе мы исследуем данный вопрос в случаях, когда  --- произвольная
--- произвольная 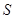 -замкнутая насыщенная формация либо
-замкнутая насыщенная формация либо 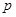 -нильпотентных, либо
-нильпотентных, либо 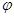 -дисперсивных, либо сверхразрешимых групп.
-дисперсивных, либо сверхразрешимых групп.
Описание конечных групп с плотной системой 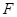 -субнормальных подгрупп для формации
-субнормальных подгрупп для формации  сверхразрешимых групп
сверхразрешимых групп
Пусть  --- произвольная
--- произвольная 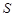 -замкнутая насыщенная формация сверхразрешимых групп,
-замкнутая насыщенная формация сверхразрешимых групп, 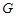 --- несверхразрешимая группа с плотной системой
--- несверхразрешимая группа с плотной системой 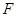 -субнормальных подгрупп. Тогда каждая
-субнормальных подгрупп. Тогда каждая 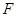 -абнормальная максимальная подгруппа из
-абнормальная максимальная подгруппа из 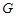 либо принадлежит
либо принадлежит 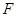 , либо является минимальной не
, либо является минимальной не 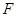 -группой, у которой нормальная силовская подгруппа является минимальной нормальной подгруппой.
-группой, у которой нормальная силовская подгруппа является минимальной нормальной подгруппой.
Доказательство. Предположим, что 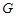 не
не 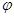 -дисперсивна, где
-дисперсивна, где 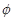 таково, что
таково, что 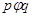 равносильно
равносильно 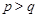 . Так как
. Так как 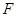 --- формация
--- формация 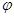 -дисперсивных групп, то, по лемме , лемма верна. Пусть теперь
-дисперсивных групп, то, по лемме , лемма верна. Пусть теперь 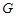
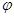 -дисперсивна. В этом случае лемма верна по лемме . Лемма доказана.
-дисперсивна. В этом случае лемма верна по лемме . Лемма доказана.
Пусть 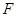 --- произвольная насыщенная
--- произвольная насыщенная 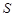 -замкнутая формация сверхразрешимых групп,
-замкнутая формация сверхразрешимых групп, 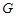 --- несверхразрешимая
--- несверхразрешимая 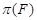 -группа с плотной системой
-группа с плотной системой 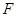 -субнормальных подгрупп. Тогда
-субнормальных подгрупп. Тогда 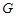 --- группа одного из следующих типов:
--- группа одного из следующих типов:
1) 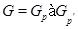 --- минимальная несверхразрешимая группа, у которой
--- минимальная несверхразрешимая группа, у которой 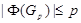 ,
, 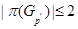 ;
;
2) 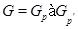 , где
, где 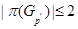 ,
, 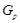 содержит такую абелеву подгруппу
содержит такую абелеву подгруппу 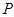 , нормальную в
, нормальную в 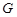 , что
, что 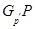 --- минимальная несверхразрешимая группа, являющаяся в
--- минимальная несверхразрешимая группа, являющаяся в 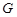 максимальной подгруппой непростого индекса, подгруппа
максимальной подгруппой непростого индекса, подгруппа 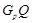 сверхразрешима, где
сверхразрешима, где 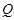 --- любая максимальная подгруппа из
--- любая максимальная подгруппа из 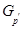 ;
;
3) 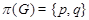 ,
, 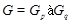 ,
, 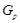 --- минимальная нормальная подгруппа группы
--- минимальная нормальная подгруппа группы 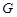 , подгруппа
, подгруппа 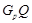 , где
, где 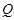 --- произвольная максимальная подгруппа из
--- произвольная максимальная подгруппа из 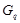 , является либо сверхразрешимой, либо минимальной не
, является либо сверхразрешимой, либо минимальной не 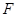 -группой, либо группой типа 2) из данной теоремы;
-группой, либо группой типа 2) из данной теоремы;
4) 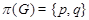 ,
, 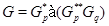 , где
, где 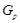 --- минимальная нормальная подгруппа группы
--- минимальная нормальная подгруппа группы 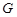 ,
, 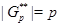 , подгруппа
, подгруппа 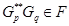 ,
, 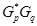 является либо минимальной несверхразрешимой группой, либо группой типа 2) из данной теоремы;
является либо минимальной несверхразрешимой группой, либо группой типа 2) из данной теоремы;
5) 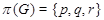 ,
, 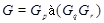 ,
, 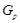 --- минимальная нормальная подгруппа из
--- минимальная нормальная подгруппа из 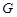 ,
, 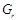 --- абелева группа,
--- абелева группа, 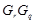 и
и 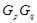 --- минимальные несверхразрешимые группы, подгруппа
--- минимальные несверхразрешимые группы, подгруппа 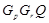 либо сверхразрешима, либо минимальная несверхразрешимая группа, где
либо сверхразрешима, либо минимальная несверхразрешимая группа, где 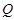 --- произвольная максимальная подгруппа из
--- произвольная максимальная подгруппа из 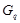 ;
;
6) 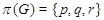 ,
, 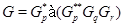 , где
, где 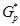 ,
, 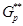 --- минимальные нормальные подгруппы группы
--- минимальные нормальные подгруппы группы 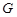 ,
, 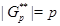 ,
, 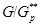 --- минимальная несверхразрешимая группа;
--- минимальная несверхразрешимая группа;
7) 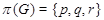 ,
, 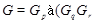 ), где
), где 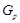 --- минимальная нормальная подгруппа группы
--- минимальная нормальная подгруппа группы 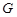 ,
, 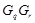 сверхразрешима, подгруппа
сверхразрешима, подгруппа 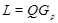 , где
, где 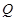 --- произвольная максимальная подгруппа группы
--- произвольная максимальная подгруппа группы 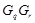 , либо сверхразрешима, либо минимальная несверхразрешимая группа, либо группа типа 2) или 4) из данной теоремы;
, либо сверхразрешима, либо минимальная несверхразрешимая группа, либо группа типа 2) или 4) из данной теоремы;
8) 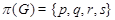 ,
, 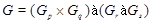 и имеет точно четыре класса максимальных сопряженных подгрупп, представителями которых являются подгруппы
и имеет точно четыре класса максимальных сопряженных подгрупп, представителями которых являются подгруппы 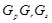 ,
, 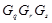 ,
, 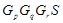 ,
, 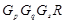 со следующими свойствами:
со следующими свойствами: 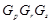 ,
, 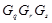 --- минимальные несверхразрешимые группы, подгруппы
--- минимальные несверхразрешимые группы, подгруппы 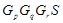 и
и 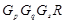 принадлежат
принадлежат 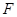 , где
, где 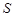 --- максимальная подгруппа из
--- максимальная подгруппа из 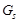 ,
, 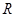 --- максимальная подгруппа из
--- максимальная подгруппа из 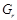 ;
;
9) 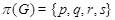 ,
, 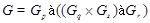 и имеет точно четыре класса максимальных сопряженных подгрупп, представителями которых являются подгруппы
и имеет точно четыре класса максимальных сопряженных подгрупп, представителями которых являются подгруппы 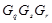 ,
, 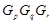 ,
, 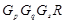 ,
, 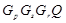 со следующими свойствами:
со следующими свойствами: 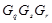 сверхразрешима,
сверхразрешима, 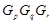 --- либо минимальная несверхразрешимая группа, либо группа типа 2) из данной теоремы,
--- либо минимальная несверхразрешимая группа, либо группа типа 2) из данной теоремы, 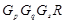 , где
, где 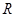 --- максимальная подгруппа из
--- максимальная подгруппа из 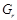 , либо принадлежит
, либо принадлежит 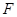 , либо
, либо 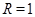 и
и 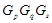 является минимальной несверхразрешимой группой или группой типа 2) из данной теоремы,
является минимальной несверхразрешимой группой или группой типа 2) из данной теоремы, 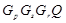 , где
, где 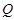 --- максимальная подгруппа из
--- максимальная подгруппа из 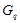 , либо принадлежит
, либо принадлежит 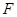 , либо
, либо 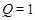 и
и 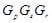 является минимальной несверхразрешимой группой или группой типа 2) из данной теоремы.
является минимальной несверхразрешимой группой или группой типа 2) из данной теоремы.
Доказательство. По лемме, группа 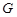 разрешима. Если группа
разрешима. Если группа 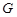 не дисперсивна по Оре, то к ней применима теорема, и данная теорема верна. Поэтому далее мы будем полагать, что группа
не дисперсивна по Оре, то к ней применима теорема, и данная теорема верна. Поэтому далее мы будем полагать, что группа 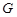 дисперсивна по Оре.
дисперсивна по Оре.
1. Рассмотрим вначале случай 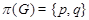 , где
, где 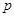 и
и 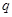 --- различные простые числа. По лемме в группе
--- различные простые числа. По лемме в группе 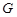 любая
любая 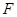 -абнормальная максимальная подгруппа либо сверхразрешима, либо является минимальной несверхразрешимой группой у которой нормальная силовская подгруппа является минимальной нормальной подгруппой. Эти два случая мы и рассмотрим.
-абнормальная максимальная подгруппа либо сверхразрешима, либо является минимальной несверхразрешимой группой у которой нормальная силовская подгруппа является минимальной нормальной подгруппой. Эти два случая мы и рассмотрим.
1.1. Пусть в 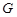 имеется несверхразрешимая
имеется несверхразрешимая 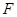 -абнормальная максимальная подгруппа
-абнормальная максимальная подгруппа 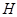 . По лемме,
. По лемме,  является минимальной несверхразрешимой группой и
является минимальной несверхразрешимой группой и 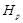 --- абелева группа. Так как
--- абелева группа. Так как 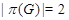 , то либо
, то либо 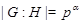 , либо
, либо 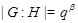 . Если предположить, что
. Если предположить, что 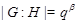 , то
, то 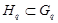 и
и 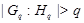 . Поэтому
. Поэтому 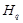 немаксимальна в
немаксимальна в 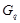 и, по лемме,
и, по лемме, 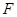 -субнормальна в
-субнормальна в 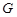 . Отсюда, по теореме ,
. Отсюда, по теореме , 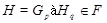 . Противоречие. Значит,
. Противоречие. Значит, 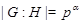 ,
, 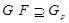 и
и 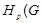 . Из того, что группа дисперсивна по Оре,
. Из того, что группа дисперсивна по Оре, 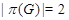 и
и 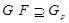 , следует, что
, следует, что 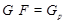 . Пусть
. Пусть 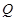 --- произвольная максимальная подгруппа из
--- произвольная максимальная подгруппа из 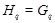 . По условию, в
. По условию, в 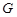 существует
существует 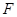 -субнормальная подгруппа
-субнормальная подгруппа 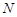 такая, что
такая, что 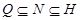 . Ясно, что
. Ясно, что 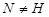 и, значит,
и, значит, 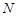 сверхразрешима. Следовательно,
сверхразрешима. Следовательно, 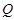
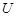 -субнормальна в
-субнормальна в 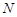 и в
и в 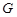 , где
, где 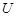 --- формация всех сверхразрешимых групп. Применяя теорему, получаем. что подгруппа
--- формация всех сверхразрешимых групп. Применяя теорему, получаем. что подгруппа 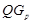 сверхразрешима. Итак, в данном случае
сверхразрешима. Итак, в данном случае 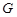 --- группа типа 2) из данной теоремы.
--- группа типа 2) из данной теоремы.
1.2. Пусть теперь в 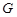 все
все 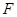 -абнормальные максимальные подгруппы сверхразрешимы. По лемме,
-абнормальные максимальные подгруппы сверхразрешимы. По лемме, 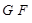 ---
--- 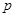 -группа. По лемме, либо
-группа. По лемме, либо 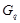 --- максимальная подгруппа в
--- максимальная подгруппа в 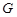 , либо
, либо 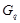 --- максимальна в
--- максимальна в 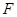 -абнормальной максимальной подгруппе
-абнормальной максимальной подгруппе 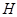 группы
группы 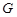 .
.
Пусть вначале 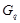 максимальна в
максимальна в 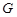 . Пусть
. Пусть 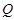 --- произвольная максимальная подгруппа из
--- произвольная максимальная подгруппа из 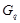 . Рассмотрим подгруппу
. Рассмотрим подгруппу 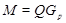 . Если
. Если


