Определение усилий в элементах металлических конструкций мостового крана

 

Мост крана принято рассчитывать как горизонтальную плоскую раму. Конструкция этой рамы – статически неопределимая система. Нормами проектирования разрешается производить упрощенные расчетные схемы с введением поправочных коэффициентов, учитывающих неточность полученных результатов.

В настоящей работе плоская рама расчленяется на отдельные балки. Коэффициент неточности (погрешности) при расчете главных балок m_∆,ГБ = 0.8, для торцевых – m_∆,ТБ = 0.5. Эти коэффициенты отображают погрешность неучета пространственной работы конструкции.

Учитывая главную особенность подъемно-транспортных машин и механизмов, в строительной механике разработан универсальный метод, который позволяет для любых систем определять наиболее невыгодное загружение подвижными нагрузками. Этот метод называется методом построения линий влияния.

Расчетное сочетание нагрузок А

Линии влияния изгибающего момента М от нагрузок вертикальной плоскости.

В данной курсовой работе построим три эпюры изгибающих моментов для точек 1, 6 и 14 см. рисунок 12.

Расчетные значения изгибающего момента в любой точке главной балки определим по формуле:

 

М_i =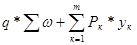

 

q – равномерно распределенная нагрузка по всей длине балке;

Р_к – постоянные, подвижные сосредоточенные нагрузки;

ω – площади линий влияния М для соответствующей точки;

y_к – ординаты линий влияния М под постоянными подвижными нагрузками.

Для точки 1 (х=1 (м)) значение изгибающего момента определяется:

 

М₁ = q * ω₁ + Р_кк * y₁^кк + Р₁ * y₁¹ + Р₂ * y₁² + Р_МП * y₁^МП.

 

Значение ординаты y₁¹ определяется:

 

y₁¹ =  =  =  = 0.96 .

 

Значение ординаты y₁² определяется:

 

y₁² =  =  =  =  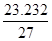= 0.86 .

 

Значение ординаты y₁^кк определяется:

 

y₁^кк =  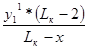=  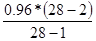=  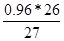=  = 0.92 .

Значение ординаты y₁^МП определяется:

 

y₁^МП =  =  =  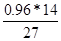=  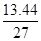= 0.50 .

 

Значение площади ω₁ определяется:

 

ω₁ =  =  =  = 13.50 .

 

Тогда получаем значение изгибающего момента М₁:

М₁ = 20 * 13.5 + 28.8 * 0.92 + 260.4 * 0.96 + 193.2 * 0.86 + 17.28 * 0.5 =

= 270 + 26.496 + 249.984 + 166.152 + 8.64 = 721.272 (кН*м).

 

Для точки 6 (х=6 (м)) значение изгибающего момента определяется:

 

М₆ = q * ω₆ + Р_кк * y₆^кк + Р₁ * y₆¹ + Р₂ * y₆² + Р_МП * y₆^МП.

 

Значение ординаты y₆¹ определяется:

 

y₆¹ =  =  =  = 4.71 .

 

Значение ординаты y₆² определяется:

 

y₆² =  =  =  =  = 4.11 .

 

Значение ординаты y₁^кк определяется:

y₆^кк =  =  =  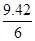= 1.57 .

 

Значение ординаты y₆^МП определяется:

 

y₆^МП =  =  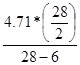=  =  = 2.99 .

 

Значение площади ω₆ определяется:

 

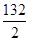ω₆ =  =  =  = 66 .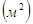

 

Тогда получаем значение изгибающего момента М₆:

М₆ = 20 * 66 + 28.8 * 1.57 + 260.4 * 4.71 + 193.2 * 4.11 + 17.28 * 2.99 =

= 1320 + 45.216 + 1226.484 + 794.052 + 51.667 = 3437.419 (кН*м).

Для точки 14 (х=14 (м)) значение изгибающего момента определяется:

 

М₁₄ = q * ω₁₄ + Р_кк * y₁₄^кк + Р₁ * y₁₄¹ + Р₂ * y₁₄² + Р_МП * y₁₄^МП.

 

Значение ординаты y₁₄¹ определяется:

 

y₁₄¹ =  =  =  = 7 .

 

Значение ординаты y₁₄² определяется:

 

y₁₄² =  =  =  =  = 5.6 .

Значение ординаты y₁₄^кк определяется:

 

y₁₄^кк =  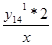=  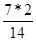=  = 1 .

 

Значение ординаты y₁₄^МП определяется:

y₁₄^МП = y₁₄¹ = 7 .

Значение площади ω₁₄ определяется:

 

ω₁₄ =  =  =  = 98 .

 

Тогда получаем значение изгибающего момента М₁₄:

М₁₄ = 20 * 98 + 28.8 * 1 + 260.4 * 7 + 193.2 * 5.6 + 17.28 * 7 =

= 1960 + 28.8 + 1822.8 + 1081.92 + 120.96 = 5014.48 (кН*м).

Линии влияния поперечной силы Q от нагрузок вертикальной плоскости

В данной курсовой работе построим три эпюры поперечной силы для точек 1, 6 и 14 см. рисунок 13.

Расчетные значения изгибающего момента в любой точке главной балки определим по формуле:

 

Q_i = 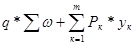, где

 

q – равномерно распределенная нагрузка по всей длине балке;

Р_к – постоянные, подвижные сосредоточенные нагрузки;

ω – площади линий влияния Q для соответствующей точки;

y_к – ординаты линий влияния Q под постоянными подвижными нагрузками.

Для точки 0 (х=0 (м)) значение поперечной силы определяется:

 

Q₀ = q * ω₀ + Р_кк * y₀^кк + Р₁ * y₀¹ + Р₂ * y₀² + Р_МП * y₀^МП.

 

Значение ординаты y₀¹ равно: y₀¹ = 1 .

Значение ординаты y₀² определяется:

 

y₀² =  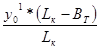=  = 0,9 .

 

Значение ординаты y₀^кк определяется:

 

y₀^кк =  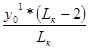=  = 0,93 .

 

Значение ординаты y₀^МП определяется:

 

y₀^МП =  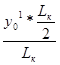=  =  = 0,5 .

 

Значение площади ω₀ определяется:

 

ω₀ =  =  =  = 14 .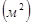

 

Тогда получаем значение поперечной силы Q₀:

Q₀ = 20 * 14 + 28.8 * 0.93 + 260.4 * 1 + 193.2 * 0.9 + 17.28 * 0.5 =

= 280 + 26.784 + 260.4 + 173.88 + 8.64 = 749.704 (кН).

Для точки 6 (х=6 (м)) значение поперечной силы определяется:

Q₆ = q * ω₆⁺ + q * ω₆^- + Р_кк * y₆^кк + Р₁ * y₆¹ + Р₂ * y₆² + Р_МП * y₆^МП.

 

Значение ординаты y₆¹⁺ определяется:

 

y₆¹⁺ =  =  =  = 0.79 .

 

Значение ординаты y₆^{1 –} определяется:

 

y₆^1- = 1 – y₆¹⁺ = 1 – 0.79 = – 0.21 , здесь знак (–) – знак координаты.

 

Значение ординаты y₆² определяется:

 

y₆² =  =  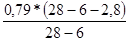=  =  = 0,69 .

 

Значение ординаты y₆^кк определяется:

 

y₆^кк =  =  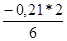= – 0.07 .

 

Значение ординаты y₆^МП определяется:

 

y₆^МП =  =  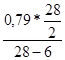=  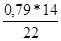= 0,5 .

 

Значение площади ω₆⁺ определяется:

ω₆⁺ =  =  =  = 8,64 .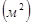

 

Значение площади ω₆ ^– определяется:

 

ω₆^- =  =  =  = – 0,64 .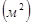

 

Тогда получаем значение поперечной силы Q₆:

Q₆ = 20 * 8,64 + 20 * (– 0,64) + 28.8 * (– 0.07) + 260.4 * 0,79 + 193.2 * 0.69 + 17.28 * 0.5 = 172,8 – 12,8 – 2,016 + 205,716 + 133,308 + 8,64 = 505.648 (кН).

Для точки 14 (х=14 (м)) значение поперечной силы определяется:

 

Q₁₄ = q * ω₁₄⁺ + q * ω₁₄^- + Р_кк * y₁₄^кк + Р₁ * y₁₄¹ + Р₂ * y₁₄² + Р_МП * y₁₄^МП.

 

Значение ординаты y₁₄¹⁺ определяется:

 

y₁₄¹⁺ =  =  =  = 0.5 .

 

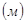Значение ординаты y₁₄^{1 –} определяется:

y₁₄^1- = 1 – y₁₄¹⁺ = 1 – 0.5 = – 0.5 , здесь знак (–) – знак координаты.

Значение ординаты y₁₄² определяется:

 

y₁₄² =  =  =  =  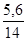= 0,4 .

 

Значение ординаты y₆^кк определяется:

y₁₄^кк =  =  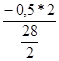= – 0.07 .

 

Значение ординаты y₁₄^МП+ определяется:

y₁₄^МП+ = y₁₄¹⁺ = 0,5 .

Значение ординаты y₁₄^{МП –} определяется:

y₁₄^МП- = y₁₄^1- = – 0.5 .

Значение площади ω₁₄⁺ определяется:

 

ω₁₄⁺ =  =  =  = 3,5 .

 

Значение площади ω₁₄ ^– определяется:

 

ω₁₄^- =  =  =  = – 3,5 .

 

Тогда получаем значение поперечной силы Q₁₄:

Q₁₄ = 20 * 3,5 + 20 * (– 3,5) + 28.8 * (– 0.07) + 260.4 * 0,5 + 193.2 * 0.4 +

+ 17.28 * 0.5 = 70 – 70 – 2,016 + 130,2 + 77,28 + 8,64 = 214.104 (кН).

Значения изгибающего момента М и поперечной силы Q от нагрузок вертикальной плоскости для сочетания А занесены в таблицу 1 расчета выполненного на ЭВМ по программе ПТМ‑у.

Линии влияния изгибающего момента М и поперечной силы Q от нагрузок горизонтальной плоскости.

Учитывая, что горизонтальные нагрузки являются сопутствующими вертикальным, эпюры линий влияния изгибающего момента М и поперечной силы Q от горизонтальных нагрузок будут полностью идентичны эпюрам от вертикальных нагрузок.

Значения изгибающего момента М и поперечной силы Q от нагрузок горизонтальной плоскости для сочетания А занесены в таблицу 1 расчета выполненного на ЭВМ по программе ПТМ‑у.

Закручивающие моменты М_кр от нагрузок горизонтальной плоскости

 

 

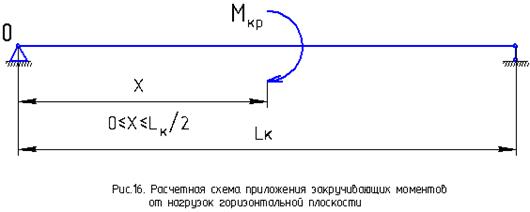
Расчетное сочетание нагрузок Б

Линии влияния изгибающего момента М от нагрузок вертикальной плоскости

Для данного сочетания эпюры изгибающего момента М от нагрузок вертикальной плоскости будут отличаться от сочетания А тем, что силы Р1 и Р2 действуют всегда слева (тележка в крайне левом положении).

Для точки 1 (х=1 (м)) значение изгибающего момента определяется:

 

М₁ = q * ω₁ + Р_кк * y₁^кк + Р₁ * y₁¹ + Р₂ * y₁² + Р_МП * y₁^МП.

 

Значение ординаты y₁¹ равно:

y₁¹ = 0 .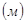

Значение ординаты y₁¹ определяется:

 

y¹ =  =  =  = 0.96 .

Значение ординаты y₁² определяется:

 

y₁² =  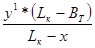=  =  =  = 0.9 .

 

Значение ординаты y₁^кк определяется:

 

y₁^кк =  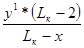=  =  =  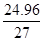= 0.92 .

 

Значение ординаты y₁^МП определяется:

 

y₁^МП =  =  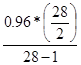=  =  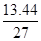= 0.50 .

 

Значение площади ω₁ определяется:

 

ω₁ =  =  =  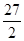= 13.50 .

 

Тогда получаем значение изгибающего момента М₁:

М₁ = 20 * 13.5 + 28.8 * 0.92 + 260.4 * 0 + 193.2 * 0.9 + 17.28 * 0.5 =

= 270 + 26.496 + 173.88 + 8.64 = 479.016 (кН*м).

Для точки 6 (х=6 (м)) значение изгибающего момента определяется:

 

М₆ = q * ω₆ + Р_кк * y₆^кк + Р₁ * y₆¹ + Р₂ * y₆² + Р_МП * y₆^МП.

 

Значение ординаты y₆¹ равно:

y₆¹ = 0 .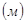

y⁶ =  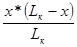=  =  = 4.71 .

 

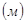Значение ординаты y₆² определяется:

 

y₆² =  =  =  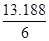= 2.20 .

 

Значение ординаты y₁^кк определяется:

 

y₆^кк =  =  =  = 1.57 .

 

Значение ординаты y₆^МП определяется:

 

y₆^МП =  =  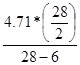=  =  = 2.99 .

 

Значение площади ω₆ определяется:

 

ω₆ =  =  =  = 66 .

 

Тогда получаем значение изгибающего момента М₆:

М₆ = 20 * 66 + 28.8 * 1.57 + 260.4 * 0 + 193.2 * 2.20 + 17.28 * 2.99 =

= 1320 + 45.216 + 425.04 + 51.667 = 1841.943 (кН*м).

Для точки 14 (х=14 (м)) значение изгибающего момента определяется:

 

М₁₄ = q * ω₁₄ + Р_кк * y₁₄^кк + Р₁ * y₁₄¹ + Р₂ * y₁₄² + Р_МП * y₁₄^МП.

Значение ординаты y₁₄¹ равно:

y₁₄¹ = 0 .

Значение ординаты y¹⁴ определяется:

 

y¹⁴ =  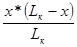=  =  = 7 .

 

Значение ординаты y₁₄² определяется:

 

y₁₄² =  =  =  = 1.4 .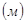

 

Значение ординаты y₁₄^кк определяется:

 

y₁₄^кк =  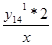=  =  = 1 .

 

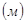Значение ординаты y₁₄^МП определяется:

y₁₄^МП = y₁₄¹ = 7 .

Значение площади ω₁₄ определяется:

 

ω₁₄ =  =  =  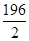= 98 .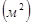

 

Тогда получаем значение изгибающего момента М₁₄:

М₁₄ = 20 * 98 + 28.8 * 1 + 260.4 * 0 + 193.2 * 1.4 + 17.28 * 7 =

= 1960 + 28.8 + 270.48 + 120.96 = 2380.24 (кН*м).

Линии влияния поперечной силы Q от нагрузок вертикальной плоскости

Для точки 0 (х=0 (м)) значение поперечной силы определяется:

Q₀ = q * ω₀ + Р_кк * y₀^кк + Р₁ * y₀¹ + Р₂ * y₀² + Р_МП * y₀^МП.

 

Значение ординаты y₀¹ равно:

y₀¹ = 1 .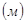

Значение ординаты y₀² определяется:

 

y₀² =  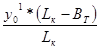=  = 0,9 .

 

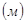Значение ординаты y₀^кк определяется:

 

y₀^кк =  =  = 0,93 .

 

Значение ординаты y₀^МП определяется:

 

y₀^МП =  =  =  = 0,5 .

 

Значение площади ω₀ определяется:

 

ω₀ =  =  =  = 14 .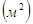

 

Тогда получаем значение поперечной силы Q₀:

Q₀ = 20 * 14 + 28.8 * 0.93 + 260.4 * 1 + 193.2 * 0.9 + 17.28 * 0.5 = 280 + 26.784 + 260.4 + 173.88 + 8.64 = 749.704 (кН).

Для точки 6 (х=6 (м)) значение поперечной силы определяется:

Q₆ = q * ω₆⁺ + q * ω₆^- + Р_кк * y₆^кк + Р₁ * y₆¹ + Р₂ * y₆² + Р_МП * y₆^МП.

 

Значение ординаты y₆¹ равно:

y₆¹ = 0 .

Значение ординаты y₆¹⁺ определяется:

 

y₆¹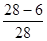⁺ =  =  =  = 0.79 .

 

Значение ординаты y₆^{1 –} определяется:

y₆^1- = 1 – y₆¹⁺ = 1 – 0.79 = – 0.21 , здесь знак (–) – знак координаты.

Значение ординаты y₆² определяется:

 

y₆² =  =  =  = – 0,10 .

 

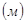Значение ординаты y₆^кк определяется:

 

y₆^кк =  =  = – 0.07 .

 

Значение ординаты y₆^МП определяется:

 

y₆^МП =  =  =  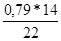= 0,5 .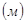

 

Значение площади ω₆⁺ определяется:

 

ω₆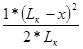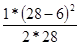⁺ =  =  =  = 8,64 .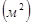

Значение площади ω₆ ^– определяется:

 

ω₆^- =  =  =  = – 0,64 .

 

Тогда получаем значение поперечной силы Q₆:

Q₆ = 20 * 8,64 + 20 * (– 0,64) + 28.8 * (– 0.07) + 260.4 * 0 + 193.2 * (– 0,10) + 17.28 * 0.5 = 172,8 – 12,8 – 2,016 – 19,32 + 8,64 = 147.304 (кН).

Для точки 14 (х=14 (м)) значение поперечной силы определяется:

 

Q₁₄ = q * ω₁₄⁺ + q * ω₁₄^- + Р_кк * y₁₄^кк + Р₁ * y₁₄¹ + Р₂ * y₁₄² + Р_МП * y₁₄^МП.

 

Значение ординаты y₆¹ равно:

y₁₄¹ = 0 .

Значение ординаты y₁₄¹⁺ равно:

 

y₁₄¹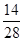⁺ =  =  =  = 0.5 .

 

Значение ординаты y₁₄^{1 –} равно:

y₁₄^1- = 1 – y₁₄¹⁺ = 1 – 0.5 = – 0.5 , здесь знак (–) – знак координаты.

Значение ординаты y₁₄² определяется:

 

y₁₄² =  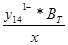=  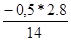=  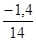= – 0,10 .

 

Значение ординаты y₆^кк определяется:

 

y₁₄^кк =  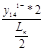=  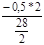= – 0.07 .

Значение ординаты y₁₄^МП+ определяется:

y₁₄^МП+ = y₁₄¹⁺ = 0,5 .

Значение ординаты y₁₄^{МП –} определяется:

y₁₄^МП- = y₁₄^1- = – 0.5 .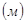

Значение площади ω₁₄⁺ определяется:

 

ω₁₄⁺ =  =  =  = 3,5 .

 

Значение площади ω₁₄ ^– определяется:

 

ω₁₄^- =  =  =  = – 3,5 .

 

Тогда получаем значение поперечной силы Q₁₄:

Q₁₄ = 20 * 3,5 + 20 * (– 3,5) + 28.8 * (– 0.07) + 260.4 * 0 + 193.2 * (– 0,10) + 17.28 * 0.5 = 70 – 70 – 2,016 – 19,32 + 8,64 = 11.296 (кН).

Значения изгибающего момента М и поперечной силы Q от нагрузок вертикальной плоскости для сочетания Б занесены в таблицу 1 расчета выполненного на ЭВМ по программе ПТМ‑у.

Усилия от перекоса крана

 

М₀ = Р_пер * L_к = 31 * 28 = 868 (кН*м).

М₆ = Р_пер * (L_к – х₆) = 31 *(28–6) = 682 (кН*м).

М₁₄ = Р_пер * L_к/2 = 31 * 28/2 = 434 (кН*м).

мост кран нагрузка балка

Определение усилий в главной балке моста крана.

Результаты приведены в таблице и нарисованы на эпюрах.