Округление промежуточных результатов вычислений

И так, мы выяснили, что часто промежуточные результаты вычислений нужно округлять, что приводит к появлению дополнительных погрешностей. Операции округления (соответственно и погрешности), зависят от способа представления чисел, используемого в вычислительном устройстве.

При использовании арифметики с фиксированной запятой операции сложения и вычитания не приводят к необходимости округления результатов — они могут вызвать лишь переполнение. Действительно, ведь количество знаков после запятой при сложении двух чисел с фиксированной запятой такое же, как было у слагаемых (слева суммируемые числа записаны в двоичной системе счисления, справа — в десятичной):

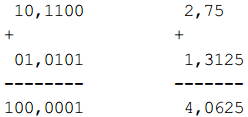
В данном примере суммируемые числа имели по 4 двоичных разряда после запятой, и столько же разрядов после запятой необходимо для представления их суммы.

А вот для представления целой части суммы нужно три разряда, тогда как для слагаемых было достаточно двух. Поэтому, если для представления целой части чисел используется два разряда, в данном случае возникнет переполнение.

В отличие от сложения, умножение чисел с фиксированной запятой приводит к увеличению числа значащих цифр результата (по сравнению с сомножителями) и, следовательно, к необходимости округления. Перемножим те же два числа, которые использовались в примере сложения:

Результат умножения в данном примере имеет 6 значащих цифр после запятой. Если для представления результата используется тот же формат, что и для сомножителей, придется производить округление:

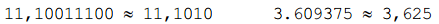
Для умножения чисел с плавающей запятой, все вышесказанное так же справедливо. Но, если результат умножения по модулю не превосходит единицы, использование формата с плавающей запятой даст большую точность, поскольку не будут зря тратиться разряды для представления незначащих нулей слева.

Однако операции сложения в формате с плавающей запятой тоже могут приводить к потере точности. Пусть рассматриваемые нами два числа представлены в формате с плавающей запятой, использующем 6 разрядов для хранения дробной части нормализованной мантиссы (мантисса и порядок записаны в двоичной системе счисления):

Представим результат сложения тоже в экспоненциальном формате:

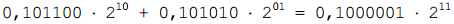
Как видите, для точного представления результата шести значащих цифр мантиссы оказалось мало, а значит, придется выполнять округление. В данном случае, когда погрешность округления в обе стороны одинакова, возможно использование различных подходов. Выберем, например, округление в большую сторону:

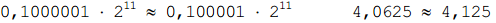
В результате при сложении чисел с плавающей запятой может не выполняться свойство ассоциативности — результат суммирования нескольких чисел может зависеть от последовательности выполнения сложений. При обучении программированию обычно дается рекомендация складывать числа, начиная с меньших (по модулю) и заканчивая самыми большими. Однако при реализации алгоритмов цифровой обработки сигналов мы, как правило, лишены возможности произвольно менять последовательность суммирования (хотя бы потому, что для сортировки слагаемых потребуется дополнительное время)