Аналитическая модель собственного шума в фильтрах с фиксированной запятой

Для статистического анализа ошибок округления, возникающих при выполнении вычислений с фиксированной запятой, в структурную схему фильтра вводятся эквивалентные источники шума, добавляемого к результатам умножения (ведь, как уже было сказано ранее, при сложении чисел с фиксированной запятой погрешностей не возникает)

Предполагается, что эти источники обладают следующими свойствами:

распределение вероятности генерируемых ими шумов является равномерным, ширина диапазона равномерного распределения равна единице младшего разряда используемого формата представления чисел;

шумовые отсчеты, генерируемые источниками, являются некоррелированными, т. е. генерируется белый шум;

шумы, генерируемые разными источниками, являются статистически независимыми;

собственные шумы фильтра и обрабатываемый полезный сигнал также являются статистически независимыми.

Условия, при которых эти предположения близки к реальности, такие же, как и для выполнения аналогичных предположений о шумах квантования сигнала — сетка уровней равномерного квантования должна быть настолько частой, чтобы значение сигнала между соседними отсчетами изменялось на несколько уровней.

Способ организации вычислений в фильтре определяется его структурной схемой, поэтому для фильтров, реализованных в разных формах, статистические свойства собственных шумов тоже будут разными. Проанализируем спектральные свойства собственных шумов для фильтров второго порядка, реализованных в прямой и канонической формах

Прямая форма

Структурная схема фильтра второго порядка, реализованного в прямой форме

Из рисунка видно, что в данном случае все пять собственных шумов являются слагаемыми общей суммы, формирующей выходной сигнал фильтра. Таким образом, шум от любого источника проходит на выход только через рекурсивную часть фильтра, так что функция передачи для любого источника шума оказывается равна

Соответствующий коэффициент передачи по мощности равен

вследствие независимости источников шумов их мощности суммируются. В итоге получаем СПМ собственного шума на выходе фильтра, равную

Где  – дисперсия каждого источника шума ( 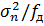 дает двустороннюю СПМ этого источника)

Каноническая форма

Структурная схема фильтра второго порядка, реализованного в канонической форме, включающая источники собственных шумов, показана на рисунке

Из рисунка видно, что шумы n_bi( k ) приложены непосредственно к выходу схемы и не проходят через какие-либо рекурсивные ветви. Что касается шумов n_ai(k), то они приложены к входу схемы и, таким образом, преобразуются в соответствии с функцией передачи фильтра.

В результате СПМ собственного шума на выходе данной схемы можно записать в виде:

где (ω) — комплексный коэффициент передачи фильтра