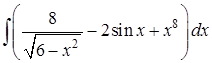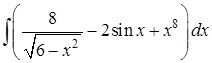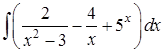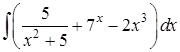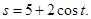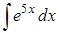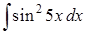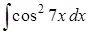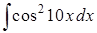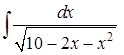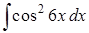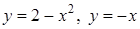Главная | О нас | Обратная связь Автоматизация Автостроение Антропология Археология Архитектура Астрономия Предпринимательство Биология Биотехнология Ботаника Бухгалтерский учет Генетика География Геология Государство Демография Деревообработка Журналистика и СМИ Зоология Изобретательство Иностранные языки Информатика Информационные системы Искусство История Кинематография Кораблестроение Кулинария Культура Лексикология Литература Логика Маркетинг Математика Математический анализ Материаловедение Машиностроение Медицина Менеджмент Металлургия Метрология Механика ОБЖ Охрана Труда Педагогика Политология Правоотношение Программирование Производство Промышленность Психология Радио Разное Социология Спорт Статистика Строительство Теология Технологии Туризм Усадьба Физика Физиология Философия Финансы Химия Черчение Экология Экономика Электротехника Алгебра и геометрия. Производные и пределы 2019-12-29 240 Обсуждений (0) Алгебра и геометрия. Производные и пределы 0.00 из 5.00 0 оценок Скачать документ 123 Задание 1. Дана матрица   Найти матрицу Задание 2. Дана система уравнений А·Х=В, где матрицы Решить систему по формулам Крамера; Значения параметров а, b, c, d к заданиям 1, 2 даны в таблице. Номер варианта a b c d Номер варианта a b c d 1 –1 1 5 –4 16 1 2 –2 4 2 2 1 4 –1 17 1 3 –2 –2 3 1 –3 1 –4 18 3 –3 1 2 4 2 1 6 1 19 –2 3 –1 1 5 1 –2 –1 6 20 1 1 5 –2 6 1 2 –2 4 21 –1 1 5 -4 7 1 3 –2 –2 22 2 1 4 –1 8 3 –3 1 2 23 1 –3 1 -4 9 –2 3 –1 1 24 2 1 6 1 10 1 1 5 –2 25 1 –2 –1 6 11 –1 1 5 –4 26 1 2 –2 4 12 2 1 4 –1 27 1 3 –2 –2 13 1 –3 1 –4 28 3 –3 1 2 14 2 1 6 1 29 –2 3 –1 1 15 1 –2 –1 6 30 1 1 5 –2   Задание 3. Даны координаты вершин треугольной пирамиды А1А2А3А4 (см. табл.). Требуется найти: а) длину ребра А1А2; б) угол между ребрами А1А2 и А1А3; в) площадь грани А1А2А3; г) объём пирамиды;   Номер варианта А1 А2 А3 А4 1 (–3, -1,5) (–4,0,1) (–2,1,3) (–2,-1,1) 2 ( 0 ,2 , 5 ) (–1,3,1) (1,4,3) (1,2,1) 3 (-2,1,2) (-3,2,-2) (–1, 3,0) (-1, 1,-2) 4 (0,-2,5) (–1,-1,1) (1,0,3) (1, -2,1) 5 (0,-1,6) (-1,0,2) (1,1,4) (1,-1,2) 6 (-2,-2,5) (–3,-1,1) (–1,0,3) (–1, -2,1) 7 (1, -1,5) (-1,-1,-1) (2,1,3) (2,-1,1) 8 (–2, 2,5) (–3, 3,1) (–1,4,3) (–1,2,1) 9 (–3, 1,3) (-4,2,-1) (–2,3,1) (-2,1,-1) 10 (0,1,6) (-1,2,2) (1,3,4) (1, 1,2) 11 (–3, -1,5) (–4,0,1) (–2,1,3) (–2,-1,1) 12 ( 0 ,2 , 5 ) (–1,3,1) (1,4,3) (1,2,1) 13 (-2,1,2) (-3,2,-2) (–1, 3,0) (-1, 1,-2) 14 (0,-2,5) (–1,-1,1) (1,0,3) (1, -2,1) 15 (0,-1,6) (-1,0,2) (1,1,4) (1,-1,2) 16 (-2,-2,5) (–3,-1,1) (–1,0,3) (–1, -2,1) 17 (1, -1,5) (-1,-1,-1) (2,1,3) (2,-1,1) 18 (–2, 2,5) (–3, 3,1) (–1,4,3) (–1,2,1) 19 (–3, 1,3) (-4,2,-1) (–2,3,1) (-2,1,-1) 20 (0,1,6) (-1,2,2) (1,3,4) (1, 1,2) 21 (–3, -1,5) (–4,0,1) (–2,1,3) (–2,-1,1) 22 ( 0 ,2 , 5 ) (–1,3,1) (1,4,3) (1,2,1) 23 (-2,1,2) (-3,2,-2) (–1, 3,0) (-1, 1,-2) 24 (0,-2,5) (–1,-1,1) (1,0,3) (1, -2,1) 25 (0,-1,6) (-1,0,2) (1,1,4) (1,-1,2) 26 (-2,-2,5) (–3,-1,1) (–1,0,3) (–1, -2,1) 27 (1, -1,5) (-1,-1,-1) (2,1,3) (2,-1,1) 28 (–2, 2,5) (–3, 3,1) (–1,4,3) (–1,2,1) 29 (–3, 1,3) (-4,2,-1) (–2,3,1) (-2,1,-1) 30 (0,1,6) (-1,2,2) (1,3,4) (1, 1,2) Задание 4.Найти производные 1-го порядка данных функций. 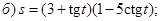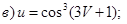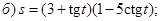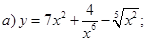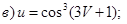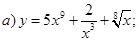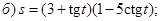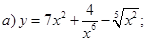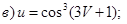1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30   Задание 5. Составить уравнение касательной и нормали к кривой y=f(x) в точке с абсциссой х0.   Номер варианта Вид функции f(x) Номер варианта Вид функции f(x) 1 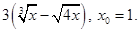16 2 17 3 18 4 19 5 20 6 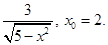21 7 22 8 23 9 24 10 25 11 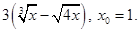26 12 27 13 28 14 29 15 30 Задание 6. Найти дифференциалы функций Номер варианта y=f(x) u=u(x) s=s(t)   1 а) 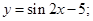б) в) 2 а) б) в) 3 а) б) в) 4 а) б) в) 5 а) 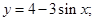б) в) 6 а) б) в) 7 а) б) в) 8 а) б) в) 9 а) б) в) 10 а) б) в) 11 а) б) в) 12 а) б) 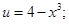в) 13 а) б) в) 14 а) б) в) 15 а) б) в) 16 а) б) в) 17 а) б) в) 18 а) б) в) 19 а) б) в) 20 а) б) в) 21 а) 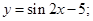б) в) 22 а) б) 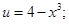в) 23 а) б) в) 24 а) б) в) 25 а) 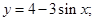б) в) 26 а) б) в) 27 а) б) в) 28 а) б) в) 29 а) б) в) 30 а) б) в)                   Задание 7. Найти пределы, используя элементарные способы раскрытия неопределенностей. 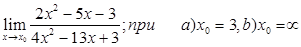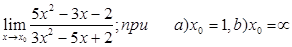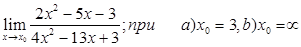1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30)   Задание 8 . Пользуясь таблицей основных интегралов и правилами интегрирования, найти интегралы. Интегралы
1	2
3	4
5	6
7	8
9	10
11	12
13	14
15	16
17	18
19	20

Задание 9. Найти интегралы

№ вар.	Интегралы
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Задание 10. Найти площадь фигуры, ограниченной линиями.

№ вар.	Уравнения линий
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Задание 11 .   Классическое определение вероятности. 

    1. Из колоды в 36 карт наудачу извлекают 3 карты. Найти вероятность того, что среди них окажется один туз.

    2. Среди 10 электрических лампочек 3 нестандартные. Найти вероят­ность того, что взятые наугад две лампочки окажутся нестандарт­ными.

    3. Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероят­ность того, что набраны нужные цифры.

    4. В партии из 12 деталей 2 бракованные. Найти вероятность того, что среди взятых наугад четырех деталей окажутся 2 бракованные.

    5. 20 участников шахматного турнира разделили на 2 команды по 10 чело­век в каждой. Найти вероятность того, что 2 сильнейших игрока окажутся в одной команде.

    6. Абонент забыл шестизначный номер телефона и набрал его наугад, помня лишь, что все цифры в нем различны. Какова вероятность набрать нужный номер?

    7. В партии из 15 телевизоров 5 имеют скрытые дефекты. Найти вероят­ность того, что 3 телевизора, выбранные наугад, не имеют скрытых дефектов.

    8. Игрок делит наугад колоду в 36 карт пополам и одну половину берет себе. Найти вероятность того, что у него окажутся все 4 туза.

    9. На шести карточках написаны цифры от 1 до 6. Найти вероятность того, что среди 3-х случайно выбранных карточек окажется карточка с номером 6.

       10. Из 10 лотерейных билетов выигрышными являются 2. Найти вероят­ность того, что среди взятых наудачу пяти билетов выигрышными являются два. 

11. Из колоды в 36 карт наудачу извлекают 2 карты. Найти вероятность того, что среди них окажется один туз.

    12. Среди 10 электрических лампочек 2 нестандартные. Найти вероят­ность того, что взятые наугад две лампочки окажутся нестандарт­ными.

    13. Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероят­ность того, что набраны нужные цифры.

    14. В партии из 12 деталей 3 бракованные. Найти вероятность того, что среди взятых наугад четырех деталей окажутся 2 бракованные.

    15. 40 участников шахматного турнира разделили на 4 команды по 10 чело­век в каждой. Найти вероятность того, что 2 сильнейших игрока окажутся в одной команде.

    16. Абонент забыл шестизначный номер телефона и набрал его наугад, помня лишь, что все цифры в нем различны. Какова вероятность набрать нужный номер?

    17. В партии из 20 телевизоров 5 имеют скрытые дефекты. Найти вероят­ность того, что 4 телевизора, выбранные наугад, не имеют скрытых дефектов.

    18. Игрок делит наугад колоду в 36 карт пополам и одну половину берет себе. Найти вероятность того, что у него окажутся все 4 туза.

    19. На шести карточках написаны цифры от 1 до 6. Найти вероятность того, что среди 3-х случайно выбранных карточек окажется карточка с номером 6.

       20. Из 20 лотерейных билетов выигрышными являются 2. Найти вероят­ность того, что среди взятых наудачу пяти билетов выигрышными являются два. 

Задание 12 .Теоремы сложения и умножения вероятностей

    1. На стройке 3 крана. Вероятность безотказной работы первого крана равна 0,7, второго – 0,8, третьего – 0,9. Найти вероятность того, что работает хотя бы один кран.

    2. Два стрелка стреляют по одной мишени. Вероятность поражения мишени первым стрелком равна 0,7, вторым – 0,8. Оба производят по одному выстрелу в мишень. Найти вероятность того, что оба стрелка поразят мишень.

    3. Для сигнализации об аварии установлено 3 независимо работа­ю­щих датчика. Вероятность срабатывания при аварии для первого датчика равна 0,9, для второго - 0,8, для третьего – 0,7. Найти вероятность, что при аварии срабо­тает хотя бы один датчик.

    4. В цехе работает два конвейера. Вероятность безотказной работы перво­го  конвейера равна 0,6, а второго – 0,8. Найти вероятность того, что в данный момент работает один конвейер.

    5. Рабочий обслуживает 3 станка. Вероятность того, что станок потребует в течение рабочего дня ремонта, для первого станка равна 0,2,­ для второго –0,1, для третьего – 0,3. Найти вероятность того, что в течение рабочего дня ни один из станков не потребует ремонта.

    6. Два стрелка делают по одному выстрелу в мишень. Вероятность попадания в нее первым стрелком равна 0,5, вторым – 0,6. Найти вероятность того, что мишень будет поражена хотя бы одним из стрелков.

    7. Устройство состоит из двух независимо работающих блоков. Вероят­ности отказа блоков соответственно равны 0,1 и 0,05. Найти ве­роят­ность отка­за устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.

    8. Найти вероятность того, что при одновременном бросании трех игральных костей, ни на одной из них не выпадет "6".

    9. В цехе работает два конвейера. Вероятность безотказной работы перво­го конвейера равна 0,6, а второго – 0,8. Найти вероятность того, что в данный момент работает хотя бы один конвейер.

    10. В магазине установлено 3 кондиционера. Вероятность быть вклю­ченным для первого кондиционера равна 0,6, для второго – 0,5, для третьего – 0,7. Найти вероятность того, что включены все три кондиционера.

11. На стройке 3 крана. Вероятность безотказной работы первого крана равна 0,75, второго – 0,85, третьего – 0,95. Найти вероятность того, что работает хотя бы один кран.

    12. Два стрелка стреляют по одной мишени. Вероятность поражения мишени первым стрелком равна 0,6, вторым – 0,7. Оба производят по одному выстрелу в мишень. Найти вероятность того, что оба стрелка поразят мишень.

    13. Для сигнализации об аварии установлено 3 независимо работа­ю­щих датчика. Вероятность срабатывания при ав

2019-12-29

240

Обсуждений (0)

Алгебра и геометрия. Производные и пределы 0.00 из 5.00 0 оценок

Скачать документ