 |
Главная |
ПОДГРУППА ФИТТИНГА И ЕЁ СВОЙСТВА
|
из
5.00
|
Произведение всех нормальных нильпотентных подгрупп группы  называют подгруппой Фиттинга группы
называют подгруппой Фиттинга группы  и обозначают через
и обозначают через  . Множество простых делителей порядка группы
. Множество простых делителей порядка группы  обозначается через
обозначается через  а наибольшую нормальную
а наибольшую нормальную  -подгруппу группы
-подгруппу группы  - через
- через  .
.
Лемма 1.1. (1)  - наибольшая нормальная нильпотентная подгруппа группы
- наибольшая нормальная нильпотентная подгруппа группы  ;
;
(2)  ;
;
(3)  .
.
Proof. (1) Пусть  и
и  - нильпотентные нормальные подгруппы группы
- нильпотентные нормальные подгруппы группы  и пусть
и пусть  и
и  - силовские
- силовские  -подгруппы из
-подгруппы из  и
и  . Так как
. Так как 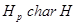 , а
, а  , то
, то  по лемме 4.1, с. 35. Аналогично,
по лемме 4.1, с. 35. Аналогично,  , поэтому
, поэтому  . Ясно,
. Ясно,  -
-  -группа. Покажем, что она силовская в
-группа. Покажем, что она силовская в  . Для этого вычислим ее индекс:
. Для этого вычислим ее индекс:


Так как числитель не делится на  , то
, то  - силовская
- силовская  -подгруппа группы
-подгруппа группы  . Итак, произведение двух нормальных нильпотентных подгрупп есть нормальная нильпотентная подгруппа. Поэтому
. Итак, произведение двух нормальных нильпотентных подгрупп есть нормальная нильпотентная подгруппа. Поэтому  - наибольшая нормальная нильпотентная подгруппа группы
- наибольшая нормальная нильпотентная подгруппа группы  .
.
(2) Ясно, что  для всех
для всех  , поэтому
, поэтому

Обратно, если  - силовская
- силовская  -подгруппа группы
-подгруппа группы  , то
, то  и
и  нормальна в
нормальна в  , поэтому
, поэтому  и
и

(3) Если  , то
, то  и
и  нильпотентна, поэтому
нильпотентна, поэтому  по (1) и
по (1) и  .
.
Лемма 1.2. (1)  ; если
; если  разрешима и
разрешима и  , то
, то  ;
;
(2) 
(3) если  , то
, то  ; если, кроме того,
; если, кроме того,  абелева, то
абелева, то 
Proof. (1) Поскольку подгруппа Фраттини  - нильпотентная нормальная подгруппа группы
- нильпотентная нормальная подгруппа группы  , то
, то  . Пусть
. Пусть  - разрешимая неединичная группа. Тогда
- разрешимая неединичная группа. Тогда  разрешима и неединична. Пусть
разрешима и неединична. Пусть

Так как  -
-  -группа для некоторого простого
-группа для некоторого простого  , то по следствию 4.2, с. 35, подгруппа
, то по следствию 4.2, с. 35, подгруппа  нильпотентна и
нильпотентна и  . Следовательно,
. Следовательно,  .
.
(2) Если  , то
, то  - нильпотентная нормальная в
- нильпотентная нормальная в  подгруппа по теореме 4.3, с. 35, поэтому
подгруппа по теореме 4.3, с. 35, поэтому  и
и

Обратное включение следует из определения подгруппы Фиттинга.
(3) Для минимальной нормальной подгруппы  либо
либо  , либо
, либо  . Если
. Если  , то
, то

Если  , то
, то  - элементарная абелева
- элементарная абелева  -группа для некоторого простого
-группа для некоторого простого  . Так как
. Так как 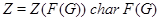 , то
, то  . С другой стороны,
. С другой стороны, 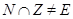 по теореме 4.4, с. 35, поэтому
по теореме 4.4, с. 35, поэтому 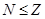 .
.
Теорема 1.3.  для любого
для любого  . В частности, если
. В частности, если  разрешима, то
разрешима, то 
Proof. Пусть 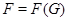 ,
,  . Так как
. Так как  по лемме 4.5, с. 35, то
по лемме 4.5, с. 35, то  . Предположим, что
. Предположим, что  для некоторого
для некоторого  и пусть
и пусть

Ясно, что  и
и 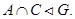 Пусть
Пусть  - силовская
- силовская  -подгруппа группы
-подгруппа группы  . Так как
. Так как

 -группа, то
-группа, то  , а поскольку
, а поскольку  , то
, то  и
и  . Теперь,
. Теперь,  - нильпотентная нормальная подгруппа группы
- нильпотентная нормальная подгруппа группы  и
и  . Таким образом,
. Таким образом,  и первое утверждение доказано. Если
и первое утверждение доказано. Если  разрешима, то
разрешима, то  разрешима, поэтому
разрешима, поэтому  и
и  .
.
Говорят, что подгруппа  группы
группы  дополняема в
дополняема в  , если существует такая подгруппа
, если существует такая подгруппа  , что
, что  и
и 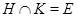 . В этом случае подгруппу
. В этом случае подгруппу 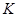 называют дополнением к подгруппе
называют дополнением к подгруппе  в группе
в группе 
Теорема 1.4. Если  - нильпотентная нормальная подгруппа группы
- нильпотентная нормальная подгруппа группы 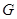 и
и 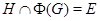 , то
, то  дополняема в
дополняема в  .
.
Proof. По условию  а по теореме 4.6, с. 35, коммутант
а по теореме 4.6, с. 35, коммутант  . По теореме 4.7, с. 35, подгруппа Фраттини
. По теореме 4.7, с. 35, подгруппа Фраттини  а по условию
а по условию  Поэтому
Поэтому  и
и  абелева. Пусть
абелева. Пусть  - добавление к
- добавление к  в
в 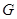 . По лемме 4.8, с. 35,
. По лемме 4.8, с. 35,  Поскольку
Поскольку  и
и  то
то  и по теореме 4.7, с. 35,
и по теореме 4.7, с. 35,

Следовательно,  и
и  - дополнение к
- дополнение к  в
в  .
.
Теорема 1.5. Факторгруппа  есть прямое произведение абелевых минимальных нормальных подгрупп группы
есть прямое произведение абелевых минимальных нормальных подгрупп группы  .
.
Proof. Предположим вначале, что  и обозначим через
и обозначим через  подгруппу Фиттинга
подгруппу Фиттинга  По теореме 4.6 коммутант
По теореме 4.6 коммутант  Но
Но  значит
значит  по теореме 4.7, с. 35. Поэтому
по теореме 4.7, с. 35. Поэтому 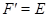 и
и  абелева. Пусть
абелева. Пусть  - прямое произведение абелевых минимальных нормальных подгрупп группы
- прямое произведение абелевых минимальных нормальных подгрупп группы 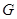 наибольшего порядка. Тогда
наибольшего порядка. Тогда  и по теореме 1.4 существует подгруппа
и по теореме 1.4 существует подгруппа  такая, что
такая, что  По тождеству Дедекинда
По тождеству Дедекинда  Но
Но  абелева, поэтому
абелева, поэтому  а так как
а так как  , то
, то  По выбору
По выбору  пересечение
пересечение  и
и 
Пусть теперь  и
и  По лемме 1.2(2)
По лемме 1.2(2) 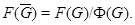 Так как
Так как  то для
то для  утверждение уже доказано.
утверждение уже доказано.
Следствие 1.6. В разрешимой группе с единичной подгруппой Фраттини подгруппа Фиттинга есть прямое произведение минимальных нормальных подгрупп. 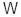
Теорема 1.7. Подгруппа Фиттинга совпадает с пересечением централизаторов главных факторов группы.
Proof. Пусть

По следствию 4.9, с. 35, подгруппа 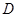 нормальна в
нормальна в  . Если
. Если

главный ряд группы  , то
, то


нормальный ряд группы  . Так как подгруппа
. Так как подгруппа  содержится в каждой подгруппе
содержится в каждой подгруппе  , то
, то

для  . По теореме 4.10, с. 35, подгруппа
. По теореме 4.10, с. 35, подгруппа  нильпотентна, поэтому
нильпотентна, поэтому  .
.
Проверим обратное включение. Пусть  - главный фактор группы
- главный фактор группы  . Так как
. Так как

то по лемме 4.11, с. 35, либо
 либо
либо 
В первом случае  , поэтому
, поэтому

Во втором случае из нильпотентности подгруппы  по лемме 1.2 получаем, что
по лемме 1.2 получаем, что

Снова  . Таким образом,
. Таким образом,  и
и  .
.
Лемма 1.8. 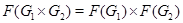 .
.
Proof. Пусть  . Ясно, что
. Ясно, что  и
и  . Так как
. Так как

то  и
и  изоморфна нормальной нильпотентной подгруппе группы
изоморфна нормальной нильпотентной подгруппе группы  . Поэтому
. Поэтому

и 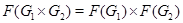 .
.
Пусть 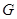 - группа и пусть
- группа и пусть




Ясно, что

В разрешимой неединичной группе подгруппа Фиттинга отлична от единичной подгруппы по лемме 1.2. Поэтому для разрешимой группы существует натуральное  такое, что
такое, что 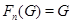 .
.
Нильпотентной длиной разрешимой группы  называют наименьшее
называют наименьшее 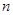 , для которого
, для которого 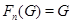 . Нильпотентную длину разрешимой группы
. Нильпотентную длину разрешимой группы  обозначают через
обозначают через  . Таким образом, если группа
. Таким образом, если группа  разрешима и
разрешима и  , то
, то

где

Поэтому построенный ряд нормальный и его факторы  нильпотентны.
нильпотентны.
Ясно, что  тогда и только тогда, когда группа
тогда и только тогда, когда группа  нильпотентна.
нильпотентна.
Пример 1.9.  .
. 
Непосредсвенно из определения нильпотентной длины вытекает
Лемма 1.10. Пусть  - разрешимая группа. Тогда:
- разрешимая группа. Тогда:
(1)  ;
;
(2)  .
. 
Лемма 1.11. (1) Если  - разрешимая группа, то длина любого нормального ряда группы
- разрешимая группа, то длина любого нормального ряда группы  с нильпотентными факторами не меньше, чем
с нильпотентными факторами не меньше, чем  .
.
(2) Нильпотентная длина разрешимой группы совпадает с длиной самого короткого нормального ряда с нильпотентными факторами.
Proof. (1) Применим индукцию по порядку группы  . Пусть
. Пусть

нормальный ряд группы  с нильпотентными факторами. Так как
с нильпотентными факторами. Так как  - нормальная нильпотентная подгруппа группы
- нормальная нильпотентная подгруппа группы  , то
, то  и
и  . Здесь
. Здесь  . Факторгруппа
. Факторгруппа  имеет порядок меньше, чем порядок группы
имеет порядок меньше, чем порядок группы  и обладает рядом
и обладает рядом

где 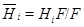 . Ясно, что это нормальный ряд, его длина
. Ясно, что это нормальный ряд, его длина  и его факторы
и его факторы
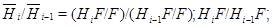

нильпотентны. По индукции  и
и  .
.
(2) следует из (1).
Лемма 1.12. Пусть  - разрешимая группа. Тогда:
- разрешимая группа. Тогда:
(1) если  , то
, то  ;
;
(2) если  , то
, то  ;
;
(3) если  и
и  , то
, то

в частности, если  и
и 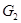 - разрешимые группы,то
- разрешимые группы,то

(4)  .
.
Proof. Пусть  и
и  . Тогда
. Тогда

(1) Пусть  . Тогда ряд
. Тогда ряд

будет нормальным рядом подгруппы  с нильпотентными факторами
с нильпотентными факторами


По лемме 1.11  .
.
(2) Пусть  и
и  . Тогда ряд
. Тогда ряд

будет нормальным рядом группы  с нильпотентными факторами
с нильпотентными факторами
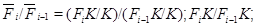

По лемме 1.10  .
.
(3) Ясно, что  . Обозначим
. Обозначим  . Тогда
. Тогда  по лемме 1.10, а по индукции
по лемме 1.10, а по индукции


Поэтому  . Так как
. Так как  по (1), то имеем
по (1), то имеем

(4) Положим  . По лемме 1.2 для неединичной разрешимой группы
. По лемме 1.2 для неединичной разрешимой группы  имеем
имеем 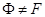 и
и

Поэтому  .
.
Следующая теорема принадлежит К. Дёрку.
Теорема 1.13. Если  - максимальная подгруппа разрешимой группы
- максимальная подгруппа разрешимой группы  , то
, то  , где
, где  .
.
Пример. Воспользуемся индукцией по порядку группы  . Пусть
. Пусть  - минимальная нормальная подгруппа группы
- минимальная нормальная подгруппа группы  . Если
. Если  , то
, то  и
и  , где
, где  . Поэтому можно предположить, что все минимальные нормальные подгруппы группы
. Поэтому можно предположить, что все минимальные нормальные подгруппы группы 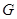 содержатся в
содержатся в  . Если группа
. Если группа  содержит две различные минимальные нормальные подгруппы, то
содержит две различные минимальные нормальные подгруппы, то  и по индукции
и по индукции

Поскольку

то теорема справедлива. Следовательно, можно считать, что группа  содержит в точности одну минимальную нормальную подгруппу. Если
содержит в точности одну минимальную нормальную подгруппу. Если  , то
, то  по лемме 1.12 и опять
по лемме 1.12 и опять

Поскольку

то опять теорема справедлива.
Итак, можно считать, что 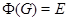 и
и  по следствию 1.6. По индукции
по следствию 1.6. По индукции

Если 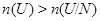 , то утверждение справедливо. Пусть
, то утверждение справедливо. Пусть  , т.е.
, т.е.  . Считаем, что
. Считаем, что  -
-  -группа. Тогда
-группа. Тогда  -
-  -группа. Пусть
-группа. Пусть  . Если
. Если  , то
, то  и
и 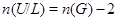 , поэтому
, поэтому

и теорема справедлива.
Остается случай, когда  . Так как
. Так как  -
-  -подгруппа, то
-подгруппа, то

причем  -
-  -группа. Противоречие.
-группа. Противоречие.
Пример 1.14.
Все три значения  в теореме 1.13 имеют место. Значение
в теореме 1.13 имеют место. Значение  выполняется на любой нильпотентной неединичной группе. Значение
выполняется на любой нильпотентной неединичной группе. Значение  выполняется на группе
выполняется на группе  с максимальной подгруппой
с максимальной подгруппой  . Значение
. Значение  выполняется на группе
выполняется на группе  , у которой силовская
, у которой силовская  -подгруппа максимальна.
-подгруппа максимальна. 
Если факторгруппа  нильпотентна, то группу
нильпотентна, то группу  называют метанильпотентной.
называют метанильпотентной.
Теорема 1.15. (1) В разрешимой неединичной группе подгруппа Фраттини совпадает с пересечением максимальных подгрупп, не содержащих подгруппу Фиттинга.
(2) В разрешимой ненильпотентной группе пересечение максимальных подгрупп, содержащих подгруппу Фиттинга, метанильпотентно.
Proof. Обозначим через  пересечение всех максимальных подгрупп группы
пересечение всех максимальных подгрупп группы  , не содержащих
, не содержащих  , а через
, а через  пересечение максимальных подгрупп группы
пересечение максимальных подгрупп группы  , содержащих
, содержащих  . Ясно, что подгруппы
. Ясно, что подгруппы  и
и  характеристические в группе
характеристические в группе 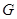 и
и

(1) В факторгруппе  подгруппа Фиттинга
подгруппа Фиттинга

по лемме 1.2, поэтому

Предположим, что  и пусть
и пусть  - минимальная нормальная подгруппа группы
- минимальная нормальная подгруппа группы 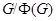 , содержащаяся в
, содержащаяся в  . Так как подгруппа
. Так как подгруппа  нормальна в группе
нормальна в группе 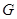 и факторгруппа
и факторгруппа  нильпотентна, то по теореме 4.3, с. 35, подгруппа
нильпотентна, то по теореме 4.3, с. 35, подгруппа 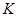 нильпотентна и
нильпотентна и  . Но теперь
. Но теперь

противоречие. Поэтому допущение неверно и  , т.е.
, т.е.  .
.
(2) Пусть  - разрешимая ненильпотентная группа. Ясно, что
- разрешимая ненильпотентная группа. Ясно, что 
 и
и

Поэтому подгруппа  метанильпотентна.
метанильпотентна.
Пример 1.16. В неразрешимой группе  центр, подгруппа Фраттини и подгруппа Фиттинга совпадают и имеют порядок
центр, подгруппа Фраттини и подгруппа Фиттинга совпадают и имеют порядок  . Поэтому в группе
. Поэтому в группе  нет максимальных подгрупп, не содержащих подгруппу Фиттинга.
нет максимальных подгрупп, не содержащих подгруппу Фиттинга.
Следовательно, утверждение (1) теоремы 1.15 в неразрешимых группах нарушается.
2  -ДЛИНА
-ДЛИНА  -РАЗРЕШИМОЙ ГРУППЫ
-РАЗРЕШИМОЙ ГРУППЫ
Пусть  - простое число. Назовем группу
- простое число. Назовем группу  -группой, если ее порядок не делится на
-группой, если ее порядок не делится на  и, как обычно,
и, как обычно,  -группой, если её порядок равен степени числа
-группой, если её порядок равен степени числа  . Конечную группу
. Конечную группу  будем называть
будем называть  -разрешимой, если каждый из её композиционных факторов является либо
-разрешимой, если каждый из её композиционных факторов является либо  -группой, либо
-группой, либо  -группой. Таким образом, группа
-группой. Таким образом, группа 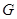 разрешима в обычном смысле тогда и только тогда, когда она
разрешима в обычном смысле тогда и только тогда, когда она  -разрешима для всех простых
-разрешима для всех простых  . Ясно, что группа
. Ясно, что группа 
 -разрешима тогда и только тогда, когда она обладает нормальным рядом
-разрешима тогда и только тогда, когда она обладает нормальным рядом

в котором каждая факторгруппа  является либо
является либо  -группой, либо
-группой, либо 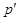 -группой. Поэтому для такой группы мы можем индуктивно определить верхний
-группой. Поэтому для такой группы мы можем индуктивно определить верхний  -ряд.
-ряд.

потребовав, чтобы  была наибольшей нормальной
была наибольшей нормальной  -подгруппой в
-подгруппой в  , а
, а  - наибольшей нормальной
- наибольшей нормальной  -подгруппой в
-подгруппой в  .
.
Наименьшее целое число  , для которого
, для которого  , мы назовем
, мы назовем  -длинной группы
-длинной группы  и обозначим его
и обозначим его  , или, если необходимо,
, или, если необходимо,  .
.
 -длину
-длину  -разрешимой группы можно также определить как наименьшее число
-разрешимой группы можно также определить как наименьшее число  -факторов, встречающихся в каком либо ряде вида (2.1), поскольку минимум достигается для верхнего
-факторов, встречающихся в каком либо ряде вида (2.1), поскольку минимум достигается для верхнего  -ряда (2.2). Подгруппы
-ряда (2.2). Подгруппы 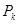 и
и  , очевидно, характеристичны в
, очевидно, характеристичны в  , и
, и  содержит все нормальные подгруппы группы
содержит все нормальные подгруппы группы  с
с  -длинной, не превосходящей числа
-длинной, не превосходящей числа 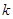 . Заметим также, что
. Заметим также, что

для 
Подгруппы и факторгруппы  -разрешимой группы
-разрешимой группы  также
также  -разрешимы, и их длина не превышает
-разрешимы, и их длина не превышает  . Если группы
. Если группы  и
и  обе
обе  -разрешимы, то таково же их прямое произведение
-разрешимы, то таково же их прямое произведение  и
и 
Пусть  -
-
|
из
5.00
|
Обсуждение в статье: ПОДГРУППА ФИТТИНГА И ЕЁ СВОЙСТВА |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

