 |
Главная |
ИСПОЛЬЗУЕМЫЕ РЕЗУЛЬТАТЫ
|
из
5.00
|
Лемма 4.1. Пусть 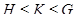 . Тогда:
. Тогда:
(1) если 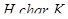 ,
, 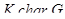 , то
, то 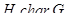 ;
;
(2) если 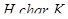 ,
, 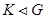 , то
, то 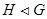 .
.
Следствие 4.2. Если 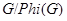 нильпотентна, то
нильпотентна, то 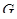 нильпотентна.
нильпотентна.
Теорема 4.3. Пусть 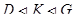 ,
, 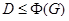 и
и 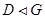 . Если
. Если 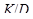 нильпотентна, то
нильпотентна, то 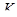 нильпотентна.
нильпотентна.
Теорема 4.4. (1) Центр 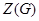 неединичной нильпотентной группы
неединичной нильпотентной группы 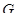 отличен от единицы и
отличен от единицы и 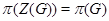 .
.
(2) В нильпотентной группе каждая собственная подгруппа отлична от своего нормализатора.
(3) В нильпотентной группе 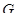 пересечение неединичной нормальной подгруппы
пересечение неединичной нормальной подгруппы 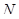 с центром группы отлично от единицы и
с центром группы отлично от единицы и 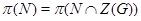 .
.
Лемма 4.5. Пусть 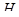 - нормальная подгруппа группы
- нормальная подгруппа группы 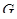 . Тогда:
. Тогда:
(1) если 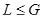 , то
, то 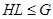 и
и 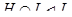 ;
;
(2) если 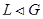 , то
, то 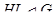 и
и 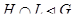 ;
;
(3) 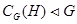 ;
;
(4) 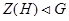 .
.
Теорема 4.6. Группа нильпотентна тогда и только тогда, когда её коммутант содержится в подгруппе Фраттини.
Теорема 4.7. Пусть 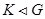 . Тогда:
. Тогда:
(1) 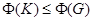 ;
;
(2) 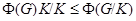 ;
;
(3) если 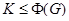 , то
, то 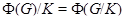 ;
;
(4) если 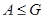 и
и 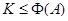 , то
, то 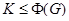 .
.
Лемма 4.8. Тогда и только тогда подгруппа 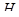 является добавлением к нормальной подгруппе
является добавлением к нормальной подгруппе 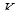 в группе
в группе 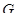 , когда
, когда 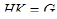 и
и 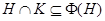 .
.
Следствие 4.9. (1) Если 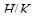 - главный фактор конечной группы
- главный фактор конечной группы 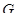 , то
, то 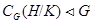 и
и 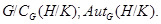
(2) Если 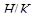 - главный фактор порядка
- главный фактор порядка 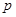 конечной группы
конечной группы 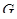 , то
, то 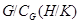 - циклическая группа порядка, делящего
- циклическая группа порядка, делящего 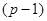 .
.
Теорема 4.10. (1) Если существует натуральное число 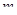 такое, что
такое, что 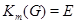 , то группа
, то группа 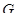 нильпотентна.
нильпотентна.
(2) Ступень нильпотентности нильпотентной группы 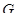 есть наименьшее натуральное число
есть наименьшее натуральное число 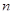 , для которого
, для которого 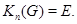
Лемма 4.11. Пусть 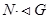 . Тогда:
. Тогда:
(1) если 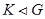 , то либо
, то либо 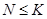 , либо
, либо 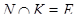 и
и 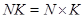 ;
;
(2) если 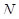 абелева и
абелева и 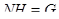 для некоторой собственной подгруппы
для некоторой собственной подгруппы 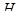 группы
группы 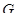 , то
, то 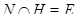 ;
;
(3) если 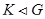 и
и 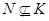 , то
, то 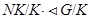 .
.
[1] Шеметков Л. А.//Докл. АН СССР. 1968. Т. 178, № 3. С. 559-662.
[2] Шеметков Л. А. Формации конечных групп. М., 1978.
[3] Hall Ph.//J. London Math. Soc. 1937. Vol. 12. P. 201-204.
[4] Черников С. Н. Группы с заданными свойствами системы подгрупп. М., 1980.
[5] Ведерников В.А. Вполне факторизуемые формации конечных групп // Вопросы алгебры. Вып.5. - Минск: Изд-во "Университетское", 1990. - С. 28-34.
[6] Ведерников В.А. Формации конечных групп с дополняемыми подформациями длины 3 // Вопросы алгебры. Вып.6. - Минск: Изд-во "Университетское", 1990. - С. 16-21.
[7] Скиба А.Н. О формациях с заданными системами подформаций // Подгрупповое строение конечных групп. - Мн.: Наука и техника, 1981. - С. 155-180.
[8] Скиба А.Н., Шеметков Л.А. Формации алгебр с дополняемыми подформациями // Укр. мат. журн. - 1991. - Т. 43, № 7, 8. - С. 1008-1012.
[9] Скиба А.Н. Алгебра формаций // Мн.: Беларуская навука, 1997. - 240 c.
[10] Черников С.Н. Группы с заданными свойствами системы подгрупп // М.: Наука, 1980. - 384 c.
[11] Guo Wenbin. Local formations in which every subformation of type 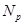 has a complement // Chinese science Bulletin. - 1997. - Vol. 42, № 5. - P. 364-368.
has a complement // Chinese science Bulletin. - 1997. - Vol. 42, № 5. - P. 364-368.
[12] Hall P. A characteristic property of soluble groups // J.London Math. Soc. - 1937. - 12. - P. 198-200.
[13] Левищенко С. С.//Некоторые вопросы теории групп. Киев, 1975. С. 173-196.
[14] Huppert B. Endliche Gruppen. I. Berlin-Heidelberg-New York, 1976.
[15] Монахов В. С.//Конечные группы. Минск, 1975. С. 70-100.
ЗАКЛЮЧЕНИЕ
В данной дипломной работе изложены основы теории нильпотентной длины конечной разрешимой группы, проведено исследование величины нильпотентной длины конечных разрешимых групп с известными добавлениями к максимальным подгруппам. В работе рассмотрены следующие вопросы: подгруппа Фиттинга конечной разрешимой группы и ее свойства; нильпотентная длина и другие инварианты конечной разрешимой группы; признаки разрешимости конечной группы с извесными добавлениями к максимальным погруппам; нахождение величины нильпотентной длины разрешимой группы с известными добавлениями к максимальным подгруппам.
В первой главе "Подгруппа Фиттинга и ее свойства" изучены свойства подгруппы Фиттинга. Доказаны теоремы К. Дёрка и Монахова В.С.
Во второй главе " 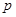 -длина
-длина 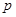 -разрешимой группы" даны необходимые определения и доказана теорема.
-разрешимой группы" даны необходимые определения и доказана теорема.
В главе "Группа с нильпотентными добавлениями к подгруппам" доказана важная теорема:
Теорема. Конечная неразрешимая группа с нильпотентными добавлениями к несверхразрешимым подгруппам изоморфна 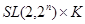 или
или 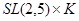 , где
, где 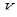 - нильпотентная группа, а
- нильпотентная группа, а  и
и 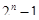 - простые числа.
- простые числа.
Также доказано следствие из этой теоремы.
Следствие. Конечная неразрешимая группа, в которой все подгруппы непримарного индекса сверх разрешимы, изоморфна 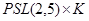 или
или 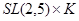 , где
, где 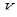 -
- 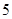 -группа, либо
-группа, либо 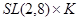 , где
, где 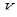 -
- 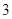 -группа.
-группа.
|
из
5.00
|
Обсуждение в статье: ИСПОЛЬЗУЕМЫЕ РЕЗУЛЬТАТЫ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

