ГЛАВА 2. Линейно упорядоченное пространство ординальных чисел.

§1.ВПОЛНЕ УПОРЯДОЧЕННЫЕ МНОЖЕСТВА И ИХ СВОЙСТВА.

Рассмотрим вполне упорядоченные множества и их свойства.

Предложение 1.1. Всякое подмножество вполне упорядоченного множества само есть вполне упорядоченное множество (очевидно).

Предложение 1.2. Если f – изоморфизм вполне упорядоченного множества А в себя, то для любого элемента х 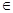А выполняется неравенство f ( x ) 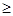x .                                                                                  (1)                            

Доказательство.

Будем доказывать методом от противного и предположим, что в А есть элементы х, не удовлетворяющие неравенству (1). Тогда среди этих элементов есть наименьший, так как А является вполне упорядоченным. Обозначим его через х₁ : f (x ₁)<x ₁ . Обозначим f (x ₁) = x ₀ и перепишем неравенство: х₀<х₁. Так как f – изоморфизм, то выполняется неравенство: f(x ₀)<f (x ₁) = x ₀ .

Таким образом, получили следующие неравенства: х₀ < x ₁ и f (x ₀) < x ₀ . Эти неравенства противоречат определению элемента х₁, как наименьшего из элементов х множества А, не удовлетворяющих условию f (x) < x. ■

Определение 2.1. Начальным отрезком, отсекаемым элементом а 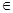А от линейно упорядоченного множества А, называется множество А_а = {x | x 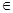A , x < a}.

Предложение 1.3. Пусть А’ – произвольное подмножество вполне упорядоченного множества А. Тогда множество А не изоморфно никакому отрезку множества А’.

Доказательство:

Будем доказывать методом от противного и предположим, что существует изоморфизм вполне упорядоченного множества А в некоторый отрезок А_х’ подмножества А’ 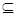А. Тогда f (x)  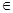A_x ’. Следовательно, f (x) < x – противоречие с предложением 1.2. ■

Следствие 1.4. Два различных отрезка вполне упорядоченного множества не могут быть изоморфны между собою.

Доказательство.

Пусть А_х и А_у – два различных отрезка вполне упорядоченного множества А. Так как А_х и А_у различны, а множество А – вполне упорядочено, то х и у сравнимы, при этом х 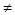у. Пусть для определённости x < y. Тогда А_х – отрезок множества А_у и по предложению 1.3 А_х и А_у не могут быть изоморфными. ■

Предложение 1.5. Существует не более одного изоморфизма одного вполне упорядоченного множества на другое.

Доказательство.

Будем доказывать методом от противного и предположим, что f и g – два различных изоморфизма вполне упорядоченного множества А на вполне упорядоченное множество В. Так как f и g различны, то существует а 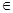А: b = f (a)  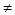b’ = g (a). Пусть для определённости b < b’. При всяком изоморфизме f множества А на множество В отрезок А_х  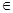А переходит в отрезок В_у  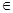В, где у = f (х). Поэтому отрезок А_а 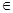А  подобен отрезкам

В _b 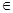 В и В _{b ’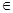} B, т. е. B_b изоморфен A_a и А_а изоморфен В _{b ’}. Следовательно, отрезок В _b  изоморфен отрезку B_{b ’} , но это противоречит следствию 1.4. ■

Определение 2.2.  Если  для  элемента  а 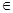 А  существует  элемент  а’ =

= inf {x | a < x , x 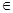A}, то а’ называется непосредственно следующим за а.

Предложение 1.6. Если А – вполне упорядоченное множество, то у каждого элемента множества А, кроме наибольшего, имеется непосредственно следующий за ним элемент.

Доказательство.

Возьмём некоторый элемент а 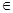А, пусть а не является наибольшим элементом. Рассмотрим множество {x | x 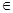A , x > а}. По предложению 1.1 оно имеет наименьший элемент а’, который является точной нижней гранью рассматриваемого множества. Следовательно, а’ следует за а. ■

            § 2. КОНЕЧНЫЕ ЦЕПИ И ИХ ПОРЯДКОВЫЕ ТИПЫ.

Предложение 2.1. Множество из n элементов можно линейно упорядочить n ! способами.

Доказательство.

Для доказательства достаточно применить формулу числа перестановок для n-элементного множества: Р_n=n! ■

Предложение 2.2.  Любое конечное линейно упорядоченное множество является вполне упорядоченным множеством.

Доказательство.

Пусть есть множество А – конечное линейно упорядоченное множество. Надо доказать, что А является вполне упорядоченным, то есть любое его подмножество имеет наименьший элемент. Рассмотрим произвольное множество В, являющееся подмножеством множества А. Предположим, что оно не имеет наименьшего элемента. Возьмём какой-нибудь элемент множества В. Обозначим его через b ₁. Так как в В нет наименьшего элемента, то в нём есть элемент b ₂, такой, что b ₂ < b ₁. Элемент b ₂ не является наименьшим элементом в В, поэтому имеется элемент b ₃<b ₂. Повторяя это рассуждение, строим для каждого натурального n элемент b_n+1 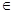 B, причём b_n+1 < b_n.

Таким образом, получили бесконечное множество {b₁, b₂, . . . ,b_n, . . } 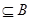, но это противоречит тому, что В – подмножество конечного множества А и, следовательно, само является конечным. ■

Предложение 2.3. Любые две конечные цепи, состоящие из n элементов, изоморфны.

Доказательство.

пусть есть две конечные цепи из n элементов:

                         a ₁ < a ₂ <…< a_n,

                         b ₁ < b ₂ <…< b_n.

Для каждого а _i  положим f (a_i) = b_i. Очевидно, что отображение f является изоморфизмом. ■

Замечание: бесконечные линейно упорядоченные множества одинаковой мощности могут и не быть изоморфными. Например, множество натуральных чисел и множество целых чисел с естественными порядками. Мощности этих множеств равны, но они не являются изоморфными, так как в N есть наименьший элемент, а в Z наименьшего элемента нет.

Определение 2.3. Порядковым типом линейно упорядоченного множества А называется класс всех линейно упорядоченных множеств, изоморфных множеству А.

Будем считать, что порядковый тип пустого множества есть 0.

Обозначим через n порядковый тип n – элементного множества

N_n = {0, 1, 2,…, n - 1} с порядком 0 < 1 < 2 <…< n-1.

                          §3.ПОРЯДКОВЫЙ ТИП .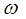

Определение 2.4. Множество натуральных чисел с естественным порядком и все изоморфные ему линейно упорядоченные множества называются множествами порядкового типа .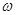

Предложение 3.1. Бесконечное линейно упорядоченное множество А имеет порядковый тип 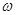 тогда и только тогда, когда оно удовлетворяет следующим условиям:

1) во множестве А имеется наименьший элемент a ₀ ;

2) для любого а 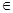А существует точная нижняя грань а’ во множестве {x | a < x , x 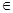A};

  3) для любого подмножества Х множества А из того, что а₀ 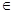Х и Х

содержит вместе с каждым своим элементом непосредственно  следующий за ним элемент, следует, что Х = А.

Доказательство.

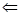 Пусть линейно упорядоченное множество А удовлетворяет условиям 1)- 3). Докажем, что А имеет порядковый тип 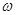, то есть А изоморфно множеству N .

Из условия (1) следует существование во множестве А наименьшего элемента а₀.

Рассмотрим отображение f: N 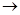 A, заданное таким образом: f (0) = a ₀,

f (n + 1) = (f (n))’, где n = 0, 1, 2,… Существование (f (n))’ для каждого n обеспечивается условием (2). Тогда вследствие условия (3) f(N)=A. Таким образом, f инъективно и сюръективно, следовательно, взаимно однозначно.       Докажем, что f сохраняет порядок: возьмём n , m 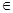 N, пусть для определённости n < m .  Из условия  (2)  следует,  что f (n) < (f (n))’  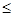f (m),

то есть f (n) < f (m). Следовательно, f сохраняет порядок.

Таким образом, f – взаимно однозначное отображение N 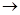 A, сохраняющее порядок. Следовательно, множество А имеет порядковый тип .

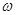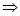 Пусть есть бесконечное линейно упорядоченное множество А, имеющее порядковый тип 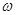. Множество N удовлетворяет условиям 1) – 3), а множество А изоморфно ему, поэтому и множество А удовлетворяет условиям 1) – 3). ■

Определение 2.5. Порядковым типом 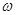^* называется класс линейно упорядоченных множеств, эквивалентных множеству N с двойственным порядком: 1 > 2 > 3 >…

Предложение 3.2. упорядоченное множество является вполне упорядоченным тогда и только тогда, когда оно не содержит подмножество типа ^*.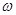

Доказательство.

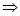 Предположим, что вполне упорядоченное множество А содержит подмножество Х типа 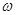^*. Тогда в Х нет наименьшего элемента, что противоречит вполне упорядоченности множества А. Следовательно, в А нет подмножеств типа ^*.

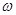 Пусть множество А не содержит подмножество типа 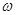^*. Докажем, что А является вполне упорядоченным множеством. Предположим, что это не так, т. е. А содержит подмножество В, в котором нет наименьшего элемента. Возьмём какой-нибудь элемент множества В, обозначим его b ₁. Так как в В нет наименьшего элемента, то существует элемент b ₂ 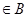, для которого b ₂ < b ₁. Повторяя это рассуждение, строим для каждого n 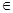N элемент b_{n +1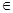}  B, причём:

                                              b_{n +1} < b_n.

Получили множество {b ₁, b ₂, … , b_n, . . .} которое является подмножеством множества А и имеет тип 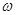^* - противоречие. ■