КАК ОПРЕДЕЛИТЬ ВЕТРОВУЮ НАГРУЗКУ, АЭРОДИНАМИЧЕСКИЙ КОЭФФИЦИЕНТ, ЧАСТОТУ

Материал этой статьи призван помочь инженерам-проектировщикам более уверенно ориентироваться в вопросах определения ветровых нагрузок по нормам проектирования СНиП.

В качестве примера в статье рассматривается конструкция мачтового типа (молниеприемник), однако алгоритм действий по сбору ветровой нагрузки будет аналогичен и для других зданий и сооружений.

Какие нагрузки действуют на молниеприемник?

Молниеприемник защищает близлежащие строения и людей от попадания разряда молнии во время грозы. Как правило, он представляет собой конструкцию мачтового или антенного типа и состоит из несущей мачты и шпиля, непосредственно принимающего электрический разряд.

Рисунок 1. Вариант исполнения молниеприемника

Определение внешних нагрузок, действующих на элементы конструкции молниеприемника, одинаково необходимо как для оценки прочности его стойки, так и для расчета фундамента (например, при подборе анкерных болтов). Такими нагрузками являются:

• собственный вес конструкции
• ветровая нагрузка
• нагрузка от наледи
• воздействие электрического разряда молнии
• особые нагрузки

В данной статье мы акцентируем внимание только на ветровых нагрузках. При этом, в своем проекте инженеру рекомендуется выполнить расчет минимум по двум сценариям:

• ветровая нагрузка действует вдоль конструкции
• ветровая нагрузка действует поперек конструкции

Дополнительными расчетными ситуациями могут быть случаи, когда ветровая нагрузка воздействует на сооружение под острым углом.

Рисунок 2. Конструктивная схема (а) и расчетная схема (б) молниеприемника

Нормативное значение ветровой нагрузки

С точки зрения механики и моделирования, ветер — достаточно сложное природное явление. Помимо прямого силового давления и быстрой изменчивости, он также обладает "раскачивающим" эффектом, т. е. даже при относительно небольшой скорости способен привести к резонансным колебаниям сооружения (и даже его разрушению).

Точный учет аэродинамической нагрузки в проектах строительных конструкций достаточно трудоемок, поэтому нормы проектирования дают приближенную методику. Так, в редакции СНиП "Нагрузки и воздействия" 2011 г. [1] значение нормативной ветровой нагрузки на 1 м² поверхности сооружения (кПа) определяется следующим образом:

wn=wm+wpwn=wm+wp, (1)

где

• wmwm — средняя составляющая ветровой нагрузки, кПа;
• wpwp — пульсационная составляющая, кПа.

Средняя составляющая ветровой нагрузки

Средняя составляющая wmwm — базовая компонента ветровой нагрузки, от которой зависит и пульсационная составляющая. Определяется она по формуле:

wm=w0⋅k⋅cwm=w0⋅k⋅c, (2)

где

• w0w0 — нормативное значение ветрового давления, кПа;
• kk — коэффициент, учитывающий изменение ветрового давления по высоте;
• cc — аэродинамический коэффициент.

Нормативное значение ветрового давления w0w0 определяется в зависимости от ветрового района. Так, для III района [1] оно составляет w0=0,30w0=0,30 кПа.

Для определения коэффициента kk существует два способа; оба из них указаны в стандарте [1]. Например, этот коэффициент можно определить по формуле

k=k10(ze10)2αk=k10(ze10)2α, (3)

где

• параметры k10k10 и αα принимаются в зависимости от типа местности (A, B или C);
• zeze — эквивалентная высота, м.

Эквивалентная высота

Эквивалентная высота конструкции используется в нормах [1] для определения различных коэффициентов.

Для башенных, мачтовых, трубных и других высотных сооружений, эквивалентная высота zeze принимается равной действительной высоте zz, т. е. расстоянию от уровня земли до точки, в которой мы определяем ветровую нагрузку:

Рисунок 3. К определению эквивалентной высоты

На элементы конструкции, расположенные на разной высоте, аэродинамическая нагрузка оказывает, в общем случае, различное воздействие. Это обстоятельство порождает простой и логичный вопрос: в каких точках прикладывать ветровую нагрузку?

Единственно правильно ответа на этот вопрос, безусловно, не существует. Любая принятая расчетчиком схема дискретизации (разделения конструкции на отдельные участки, сегменты) приближает модель к работе реальной конструкции, в большей или меньшей степени. Очевидно, модель приложения ветровой нагрузки по всей высоте поверхности (рис. 3, а) может быть принята только в первом приближении, для относительно невысоких сооружений. Более точно определить ветровую нагрузку можно, разделяя конструкцию на отдельные участки по высоте и определяя равнодействующую ww в пределах каждого участка (рис. 3, б).

В любом случае, равнодействующая должна быть приложена в центре тяжести распределенной ветровой нагрузки. Расстояние от уровня земли до этой равнодействующей и будет составлять эквивалентную высоту zeze.

Если принять схему молниеприемника по рис. 3 (а), то при общей высоте 17 м равнодействующая ветровой нагрузки будет приложена в точке ze=0,5H=8,5ze=0,5H=8,5 м. Если сооружение размещено в черте города с плотной застройкой (здания выше 25 м, тип местности C), то коэффициент kk будет равен:

k=k10(ze10)2α=k=k10(ze10)2α= 0,4(8,510)2⋅0,25=0,369.0,4(8,510)2⋅0,25=0,369. (4)

Аэродинамический коэффициент

Для определения аэродинамического коэффициента cc, входящего в (2), нередко прибегают к натурным испытаниям масштабных образцов в аэродинамической трубе. Это делается с целью получить более точную картину обтекания конструкции ветровым потоком, а также учесть шероховатость поверхности и другие аспекты конкретного сооружения.

В практических же расчетах можно руководствоваться справочной литературой. В частности, в [2] приводится следующая информация об аэродинамических коэффициентах:

Рисунок 4. Фрагмент таблицы 3.1 для определения аэродинамических коэффициентов [2]

Если направление ветрового потока совпадает с осью стенки двутаврового профиля, то аэродинамический коэффициент c=0,9c=0,9. Если же поперечное сечение конструкции представляет собой многоугольник с nn гранями, то можно воспользоваться следующими данными:

Рисунок 5. Фрагмент таблицы 3.4 для определения аэродинамических коэффициентов [2]

Таким образом, средняя составляющая ветровой нагрузки на молниеприемник двутаврового сечения (2) составляет:

wm=w0⋅k⋅c=wm=w0⋅k⋅c= 0,3⋅0,369⋅0,9=0,10,3⋅0,369⋅0,9=0,1 кПа. (5)

Пульсационная составляющая ветровой нагрузки

Пульсационная составляющая wpwp базируется на ранее определенном среднем значении ветровой нагрузки wmwm (5), но зависит также от частоты собственных колебаний конструкции. Чтобы определить эту частоту, необходимо представить молниеприемник как систему:

• с конечным числом степеней свободы (дискретная модель)
• с бесконечным числом степеней свободы (континуальная модель)

Динамический расчет можно вести и в дискретной, и в континуальной постановках. Инженерам, которые привыкли работать в САПР на основе метода конечных элементов, я бы рекомендовал применить традиционную дискретную модель с равномерным распределением сосредоточенных масс по высоте конструкции. Однако следует помнить, что МКЭ относится к численным (а значит, приближенным) методам анализа строительных конструкций. Более точное значение частоты собственных колебаний можно получить аналитически, если расчетная схема относительно проста и позволяет это сделать "вручную".

Частота собственных колебаний

На динамическое и статическое поведение конструкции в значительной степени влияет способ его опирания. Если принять расчетную схему молниеприемника в виде вертикального стержня, база которого жестко соединяется с фундаментом анкерными болтами (рис. 2, б), то частота свободных колебаний такой консольной системы равна [3]:

ω=λ2EJym0l4−−−−√ω=λ2EJym0l4, (6)

где

• λλ — частотный параметр; для первой частоты свободных колебаний консольной балки λ=1,875λ=1,875;
• EE — модуль упругости материала; для стали E=2×105E=2×105 МПа;
• JyJy — главный центральный момент инерции поперечного сечения относительно оси изгиба yy (рис. 2), см⁴;
• m0m0 — масса, распределенная по длине балки (погонная масса);
• ll — длина консольной балки, м.

Жесткость и масса молниеприемника

Пусть молниеприемник имеет поперечное сечение в форме двутавра № 40, по ГОСТ 8239-89.

В этом случае, момент инерции сечения составляет Jy=19062,0Jy=19062,0 см⁴. Если же Вы рассматриваете изгиб конструкции в перпендикулярном направлении (когда ветер воздействует вдоль оси сечения yy), то в формулу (6) следует подставить момент инерции Jz=667,0Jz=667,0 см⁴.

Единицы измерения погонной массы m0m0, входящей в формулу (6), должны совпадать с единицами измерения остальных параметров, входящих в эту же формулу. Согласно сортамента, масса двутавра № 40 составляет 57,0 кг/м, тогда частота свободных колебаний молниеприемника по первой форме равна:

ω=1,8752×ω=1,8752× 2×105×106⋅19062×10−857⋅174−−−−−−−−−−−−−−√=9,949.2×105×106⋅19062×10−857⋅174=9,949. (7).

Мы получили значение круговой частоты колебаний. Чтобы получить значение линейной частоты, выполним несложное преобразование:

f=ω2π=9,9492⋅3,142=1,583f=ω2π=9,9492⋅3,142=1,583 Гц. (8)

А вот результаты модального анализа этой же конструкции в программе Autodesk Robot Structural Analysis Professional 2017 (модель из шести конечных элементов равной длины):

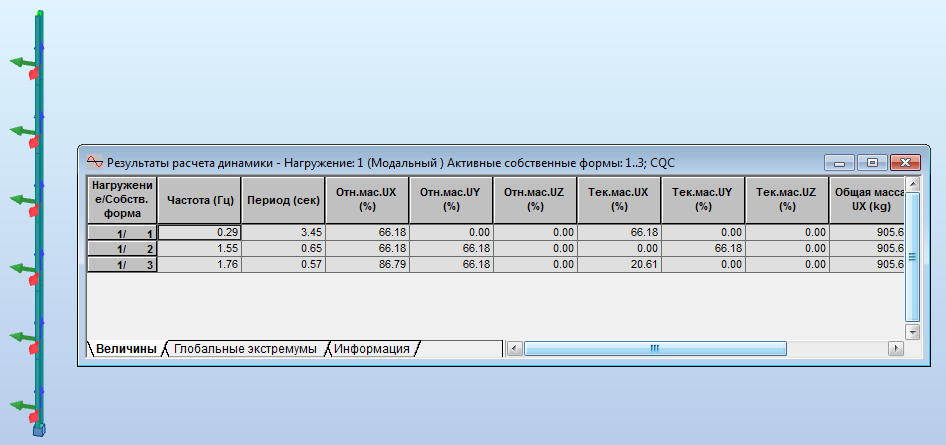
Рисунок 6. Динамический расчет стойки молниеприемника МКЭ

Аналитическое решение f=1,58f=1,58 весьма неплохо соотносится с решением методом конечных элементов (1,55 Гц). Точность решения МКЭ будет возрастать по мере сгущения конечно-элементной сетки, но не бесконечно.

Частота 0,29 Гц соответствует изгибу молниеприемника в другом, "менее жестком" направлении. Вы получите это значение, если подставите в формулу (7) меньший момент инерции сечения.

Сравнение частоты с предельным значением

Далее, полученное значение частоты следует сравнить с предельным значением частоты колебаний flimflim, которое зависит от логарифмического декремента колебаний δδ [1]. Для стальных конструкций логарифмический декремент колебаний δ=0,15δ=0,15.

С учетом III ветрового района, предельное значение частоты

flim=3,8flim=3,8 Гц.

Так как частота свободных колебаний молниеприемника f=1,58f=1,58 оказалась меньше предельного значения flim=3,8flim=3,8, то формула (11.5) СНиП "Нагрузки и воздействия" — неприменима, и следует определить вторую частоту собственных колебаний. Она определяется по тем же формулам (6) и (8), только частотный параметр теперь имеет значение

λ=4,694λ=4,694. (9)

Подставляя (9) в (6), имеем круговую частоту:

ω=4,6942×ω=4,6942× 2×105×106⋅19062×10−857⋅174−−−−−−−−−−−−−−√=62,4.2×105×106⋅19062×10−857⋅174=62,4. (10)

Линейная частота собственных колебаний молниеприемника по второй форме составляет:

f=ω2π=62,42⋅3,142=9,92f=ω2π=62,42⋅3,142=9,92 Гц. (11)

Вторая частота собственных колебаний f=9,92f=9,92 оказалась больше предельного значения flim=3,8flim=3,8, поэтому пульсационная составляющая ветровой нагрузки может быть определена по формуле [1]:

wp=wm⋅ξ⋅ζ⋅νwp=wm⋅ξ⋅ζ⋅ν, (12)

где

• ξξ (читается "кси") — коэффициент динамичности;
• ζζ (читается "дзета") — коэффициент пульсации ветра;
• νν (читается "ню") — коэффициент пространственной корреляции пульсаций давления ветра.

Коэффициент динамичности

Для определения коэффициента динамичности следует вычислить параметр

ε1=w0⋅k⋅γf√940f1ε1=w0⋅k⋅γf940f1, (13)

где

• w0=300w0=300 — нормативное значение ветрового давления, принимаемое в Па;
• γf=1,4γf=1,4 — коэффициент надежности по ветровой нагрузке;
• f1f1 — частота первой формы собственных колебаний (8).

Таким образом, параметр ε1ε1 равен

ε1=w0⋅k⋅γf√940f1=ε1=w0⋅k⋅γf940f1= 300⋅0,369⋅1,4√940⋅1,583=0,01300⋅0,369⋅1,4940⋅1,583=0,01. (14)

По рисунку 11.1 СНиП "Нагрузки и воздействия" [1], коэффициент динамичности ξ=1,5ξ=1,5.

Коэффициент пульсации

Коэффициент пульсации ветра можно определить по формуле:

ζ=ζ10(ze10)−αζ=ζ10(ze10)−α, (15)

где

• коэффициент ζ10=1,78ζ10=1,78 для местности типа C;
• ze=8,5ze=8,5 — эквивалентная высота, м;
• параметр α=0,25α=0,25 для местности типа C.

Таким образом, коэффициент пульсации ветра равен

ζ=ζ10(ze10)−α=ζ=ζ10(ze10)−α= 1,78(8,510)−0,25=1,8541,78(8,510)−0,25=1,854. (16)

Коэффициент пространственной корреляции давления

Коэффициент пространственной корреляции νν зависит от направления ветра. Таким образом, расчетчику нужно контролировать размеры поверхности, обдуваемой ветром, и выбирать соответствующие данные из таблицы 11.6 [1]. Важными здесь являются два параметра:

• χχ (читается "хи")
• ρρ (читается "ро")

Для сплошных конструкций постоянного сечения, расчетная поверхность которых перпендикулярна ветровому потоку и представляет собой прямоугольник (самый тривиальный случай), параметры ρρ и χχ равны, соответственно, ширине и высоте этой рабочей поверхности. В нашем случае:

ρ=b=0,4ρ=b=0,4 м; χ=H=17,0χ=H=17,0 м. (17)

Выполняя линейную перекрестную интерполяцию, получаем значение коэффициента:

ν=0,89ν=0,89. (18)

Таким образом, пульсационная составляющая ветровой нагрузки составляет

wp=wm⋅ξ⋅ζ⋅ν=wp=wm⋅ξ⋅ζ⋅ν= 0,1⋅1,5⋅1,854⋅0,89=0,2480,1⋅1,5⋅1,854⋅0,89=0,248 кПа. (19)

Расчетное значение ветровой нагрузки

Нормативное значение ветровой нагрузки (1) составляет:

wn=wm+wp=wn=wm+wp= 0,1+0,248=0,3480,1+0,248=0,348 кПа. (20)

Итоговое расчетное значение ветровой нагрузки, по которому далее будут определяться усилия в сечениях молниеприемника, основано на нормативной величине, с учетом коэффициента надежности:

w=wn⋅γf=w=wn⋅γf= 0,348⋅1,4=0,4870,348⋅1,4=0,487 кПа. (21)