Теоретические сведения

Лабораторная (контрольная) работа №5

Построение линейной функции регрессии по опытным данным

Методические указания

Направление подготовки: 15_04_04

Форма обучения: очная

Тула 2019

Цель и задачи работы

Научить пользоваться методом наименьших квадратов для построения по опытным данным зависимостей между показателем качества и значением управляемого фактора.

Теоретические сведения

    Метод наименьших квадратов широко используется на практике для получения зависимостей между показателем технологического процесса и влияющих на него факторов. Предполагается, что эта связь в общем случае стохастическая, то есть конкретному значению отмеченных факторов отвечает не одно значение показателя, а случайная величина, имеющая спектр возможных значений, характеризуемый соответствующим законом распределения.

    Рассмотрим случай, когда показатель технологического процесса Y зависит от фактора X и нужно опытным путем определить вид этой зависимости. Зависимость стохастическая из-за влияния неконтролируемых факторов, помех, ошибок измерения и др., поэтому на практике часто ограничиваются нахождением зависимости среднего значения показателя Y (будем отмечать его четой сверху) от значения фактора X. Эту зависимость принято называть регрессией. С точки зрения теории вероятностей в данном случае регрессия это условное математическое ожидание Y   при условии, что Х= x. Таким образом, будем искать функцию

.

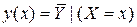Функция регрессии X на Y называется линейной, если она представляется в виде

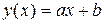                                          ,                                                (1)

где a и b – параметры, которые оцениваются по опытным данным.

    Если имеется выборка опытных данных

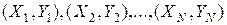                                          ,                        (2)

где N – размер выборки, то по методу наименьших квадратов параметры a и b функции регрессии (1) выбираются так, чтобы средний квадрат разности  

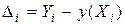
 был минимальным (см.рис.1).

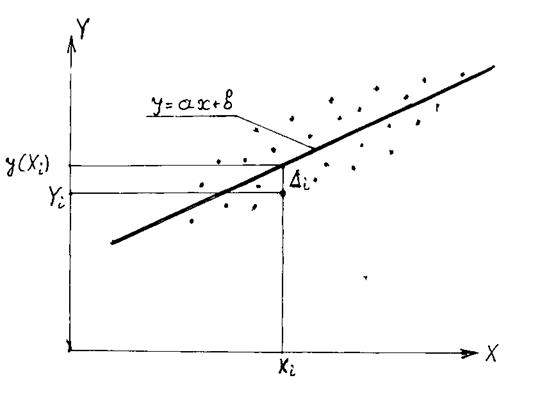
Рис.1. Иллюстрация к методу наименьших квадратов

То есть должно стать минимальным выражение

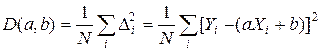.              (3)

Это значит, что частные производные по а и по b должны быть равны нулю, то есть

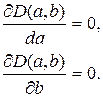
После дифференцирования получаем следующие два уравнения:

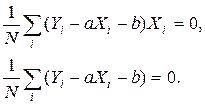
После приведения подобных получаем:

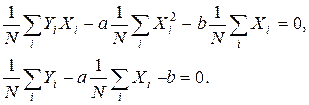
Полученная система линейна относительно a и b . Коэффициенты системы являются статистическими моментами, поэтому для них введем обозначения:

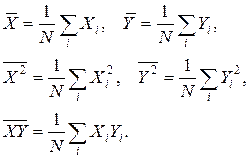                              (4)

С учетом этих обозначений получаем систему в следующем виде:

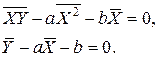                             (5)

В результате решения этой системы получаем:

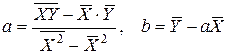.                        (6)

Если учесть, что выражение в числителе есть статистический корреляционный момент, а в знаменателе – статистическая дисперсия, то (6) перепишется так:

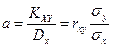,                                     (7)

где

-

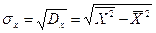
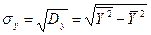Безусловные квадратичные отклонения X и Y соответственно.

-

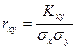коэффициент корреляции между X и Y.

 С учетом этого получаем для функции регрессии (1) следующее окончательное выражение:

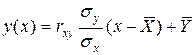.                              (8)

    Квадратичная ошибка, с которой функция регрессии (6) определяет фактическое значение Y  при условии, что X = x ,

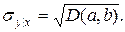
После подстановки в (2) оптимальных значений оценок a и b и проведения необходимых преобразований получаем, что

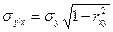.                                     (9)