Алгоритмы методов прямого поиска оптимума

для функции N переменных

А. Метод покоординатного спуска.

1. Выбрать точку x⁰, k = 0.

2. На k-й итерации: из точки x^k произвести поиск минимума вдоль направления оси x₁ и найти точку x^k1. Произвести поиск из точки x^k1 в направлении к оси x₂ и определить точку x^k2. Выполнить эту процедуру по всем координатам.

Б. Симплексный метод.

1. Выбрать базовую точку x⁰. Задать масштабный множитель a. Вычислить

.

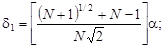
Определим остальные вершины симплекса:

 i, j =1, 2, …N.

2. На k-й итерации: определить , где x ^j - вершина с наибольшим значением функции. Отразить x ^j  относительно x_c.  x = 2 x_c – x ^j;

3. Тест на остановку: если выполнено, то конец. Если не выполнено условие сходимости или некоторая вершина не исключается на протяжении более чем M = 1,65N + 0,05N ² итерации, то необходимо уменьшить размеры симплекса, построить новый симплекс, выбрав в качестве базовой точку, которой соответствует минимальное значение целевой функции, и перейти к 2.

В. Метод Нелдера–Мида

1. Выбрать x₁, …, x_N+1, a, b, g. Вычислить f₁, …, f_N+1.

2. Найти x_h, x_g, x_z, f_h, f_g, f_z; f_h - наибольшее, f_g - следующее за ним, f_z - наименьшее значение функции.

3. Найти

4. Найти x_r, f_r, отразив точку x_h относительно x₀:

x_r = (1 + a) x₀ – ax_h .

5. Если f_r < f_z, то производим растяжение симплекса – находим  x_e = gx_r + (t – g) x₀, f_e = f(x_e).

6. Если f_e < f_z, то x_h := x_e.

Проверка на сходимость. Если сходимость достигнута, то конец. В противном случае перейти на шаг 2.

7. Если f_e ≥ f_z, то x_h := x_r.

Проверка на сходимость. Если сходимость достигнута, то конец. B противном случае перейти на шаг 3.

8. Если f_r > f_z, нo f_r £ f_g, то x_h := x_r.

Проверка на сходимость. Если сходимость не достигнута, то возвратиться на шаг 2.

9. Если f_r > f_z  и f_r > f_g, то перейти на шаг 10.

10. Если f_r > f_h, то перейти к 11.

       Если f_r < f_h, то x_h := x_r и f_h := f_r. Перейти к 11.

11. Так как f_r > f_h, то переходим к шагу сжатия:

x_c = b x_h + (1 – b)x₀.

12. Если f_c < f_h, то x_h := x_c, и если сходимость не достигнута, то возвратиться на шаг 2.

13. Если f_c > f_h, то перейти на шаг 14.

14. Уменьшить размерность симплекса x_i := (x_i + x_z)/2. Вычислить f_i для i = 1, N + 1. Проверка на сходимость. Если она не достигнута, возвратиться на шаг 3.

Г. Метод Хука–Дживса:

1. Определить начальную точку x⁰, приращение D_i, i = 1, N.

Коэффициент уменьшения шага a > 1, параметр окончания поиска E.

2. Провести исследовательский поиск.

3. Если исследовательский поиск удачный (найдена точка с меньшим значением целевой функции), перейти к 5. Иначе перейти к 4.

4. Тест на остановку: если выполнено, то конец. Иначе: уменьшить приращение.

, перейти к шагу 2.

5. Провести поиск по образцу

x_p^(K+1) = x^K + (x^K – x^K–1).

6. Провести исследующий поиск, используя x_p^K+1 в качестве базовой точки. Пусть x^K+1 - полученная в результате точка.

7). Если выполняется неравенство f(x^K+1) < f(x^K), то положить   x^K–1 = x^K и x^K= x^K+1. Перейти к 5. Иначе: перейти к 4.

Основные обозначения:

x^K - текущая базовая точка;

x^K–1 - предыдущая базовая точка;

x_p^K+1  - точка, построенная при движении по образцу;

x^K+1 - следующая (новая) базовая точка.