Критерии проверки сходимости

1. 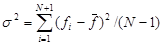; ; s < e (метод Нелдера–Мида).

2. h < e (метод Хука–Дживса), h–шаг.

Контрольные вопросы и задания

1. Назовите достоинства и недостатки прямых методов поиска для функций и переменных.

2. В чем преимущество метода Хука–Дживса по сравнению с методом покоординатного спуска?

3. В каких случаях удобно использовать симплексный метод?

4. Обеспечивают ли эти методы глобальную сходимость?

5. Для решения каких задач целесообразно использовать метод Нелдера–Мида?

6. Дайте геометрическую иллюстрацию всех четырех методов оптимизации.

7. Какой из приведенных методов целесообразно использовать для оптимизации технологических процессов в условиях производства?

 

Задание к лабораторной работе

Найти минимум функций:

1) F(x₁, x₂) = N(x₂ – x₁²)² + (N – x₁)²

2) F(x₁, x₂, x₃, x₄) = (x₁ + Nx₂)² + N(x₃ – x₄)² + (x₂ – Nx₃)⁴ +

+N(x₁ – x₄)⁴ с точностями EPS=1E-3, 1E-5, 1E-10, 1E-15.

 

Отчет о работе

1. Титульный лист.

2. Задание к лабораторной работе.

3. Алгоритмы численного нахождения минимума.

4. Графики зависимости количества итерации от точности решения.

5. Краткий анализ результатов поиска минимума указан­ных выше функций.

6. Вывод по работе.

Список методов

1. Метод покоординатного спуска.

2. Симплекс метод.

3. Метод Нелдера–Мида.

4. Метод Хука–Дживса.

Выбор метода решения

1. Порядковый номер студента в журнале по модулю 4.

2. Номер первого метода +5 по модулю 4.

 

Список рекомендуемой литературы

1. Карманов В.Г. Математическое программирование. М.: Наука, 1980.

2. Банди Б. Метод оптимизации: Вводный курс: Пер. с англ. М.: Радио и связь, 1988.

 

Лабораторная работа 3

Численные методы для оптимизации

дифференцируемых функций

 

Описание алгоритмов

А. Алгоритм градиента с заранее заданным шагом.

1. Выбрать начальную точку x⁰ и число l > 0. Положить k = 0.

2. На k-й итерации 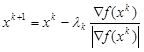, где Ñ_k; l_k > 0.

3. Тест на остановку: если выполнен, то конец. Иначе: выполнить k k+1 и возвратиться к 2.

Б. Алгоритм наискорейшего спуска.

1. Выбрать начальную точку x⁰. Положить k = 0.

2. На k-й итерации d_k = – Ñf(x^k). Найти такое число l_k, что f(x^k + l_k d_k) = min{f(x^k + ld_k)}. Положить x^k+1 = x^k + l_k d_k;

3. Тест на остановку: если выполнен, то конец. Иначе: выполнить k k+1  и возвратиться к 2.

В. Алгоритм сопряженного градиента для квадратичных функ­ций.

1. Выбрать начальную точку x⁰. Определить g = Ñq(x⁰) = Ax⁰ + b.

Положить d₀ = – g₀, k = 0.

2. На k-й итерации определить

, x^k+1 = x^k + l_k d_k, g_k+1 = Ñq(x^k+1), , d_k = – g_kH + b_k d_k.

3. Тест на остановку: если выполнен, то конец. Иначе: выполнить k k+1 и возвратиться к 2.

Г. Алгоритм Фленча–Ривза.

1. Выбрать начальную точку x⁰. Положить d₀ = – Ñf(x⁰), K = 0.

2. На K-й итерации выбрать l, минимизирующую функ­цию g(l)= =f(x_K^K + ld), положить x^K+1 = x^K + l_K d_K;

;

d_K = – Ñf(x^K+1)+ b_K d_K.

3. Тест на остановку: если выполнен, то конец. Иначе: выполнить k k+1 и возвратиться к 2.

Д. Алгоритм метода Ньютона, модифицированного метода Нью­тона, метода Марквардта.

1. Выбрать начальную точку x⁰, K = 0.

2. На K-й итерации для метода Ньютона - x^K+1 = x^K – [Ѳf(x^K)]^–1Ñf(x^K);

для модифицированного метода Ньютона x^K+1 = x^K – l_K[Ѳf(x^K)]^–1Ñf(x^K);

для метода Марквардта x^K+1 = x^K –[mI + Ѳf(x^K)]²Ñf(x^K), где m₀ = 10⁴; m_K=m₀/K.

3. Тест на остановку: если выполнен, то конец. Иначе: выполнить k k+1 и возвратиться к 2.

Е. Алгоритм Давида–Флетчера–Пауэлла (ДФП).

1. Выбрать начальную точку x⁰; положить Н₀=I, где I- единичная матрица; K=0;

2. На  K-й  итерации d_K = – H_KÑf(x^K). Найти такое l ³ 0,  чтобы

f(x^K + l_K d_K) = min{f(x^K + ld_K)}.

Положить x^K+1 = x^K  + l_K d_K; s_K = x^K+1 – x^K; g_K = Ñf(x^K+1) – Ñf(x^K);

.

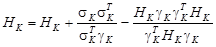3. Тест на остановку: если выполнен, то конец. Иначе: выполнить k k+1 и возвратиться к 2.

Ж. Алгоритм Бройдена–Флетчера–Гольдфарба–Шанно (БФГШ).

1. Выбрать начальную точку x⁰. Положить Н = I, где I- единичная матрица; K = 0.

2. На K-й итерации d_K = – H_KÑf(x^K).

Найти такое l ³ 0, чтобы f(x^K + l_K d_K) = min{f(x^K + ld_K)}. Положить x^K+1 = x^K  + l_K d_K; s_K = x^K+1 – x^K;  g_K = Ñf(x^K+1) – Ñf(x^K),

.

3. Тест на остановку: если выполнен, то конец. Иначе: выполнить k k+1 и возвратиться к 2.