|
Главная |
Частично упорядоченные множества
|
из
5.00
|
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
НИЖНЕКАМСКИЙ МУНИЦИПАЛЬНЫЙ ИНСТИТУТ
Кафедра информатики математики и естественно –
научных дисциплин
Группа 561
РЕФЕРАТ
По дисциплине «Абстрактная алгебра»
Уровень образования специалист
Тема: Упорядоченные множества
Руководитель ___________________ Р.М. Мунипов
Студент ___________________ А.В. Глазунов
Нижнекамск 2007
СОДЕРЖАНИЕ
ВВЕДЕНИЕ………………………………………………………………..3
1. Частично упорядоченные множества…………………………………5
2. Вполне упорядоченные множества…………………………………..20
3. Частичные группоиды и их свойства………………………………..23
ЗАКЛЮЧЕНИЕ…………………………………………………………..35
СПИСОК ЛИТЕРАТУРЫ……………………………………………….36
Введение
В настоящее время алгебра понимается в основном как общая теория алгебраических операций и отношений. Ее характеризует большая внутренняя естественность исходных идей и задач, единство методов, далеко идущая широта основных понятий. Ее область очерчена четко и ясно. И все же существующие границы теории нельзя признать установленными прочно и окончательно. Все чаще начинает выявляться стремление выйти за ее пределы. Ощущается потребность рассматривать операции не только полные, но и частичные.
Теория частичных действий естественно должна продолжать теорию полных действий. Эта последняя в настоящее время является крайне разветвленной, богатой и находится в периоде своего расцвета. Естественно возникает мысль о перенесении выработанных там понятий и результатов в новую область. Это, разумеется, необходимо и во многих случаях плодотворно. Однако уже с первых шагов развития теории частичных действий дает себя знать значительная специфика этого направления. Часто прямое перенесение результатов теории полных действий оказывается затруднительным или даже невозможным. Привычный алгебраический материал приходится подвергать существенной переработке или переосмыслению, кроме того, возникают совсем новые понятия и задачи, специфические для нового направления. Для них требуется своя методика исследования.
Таким образом, теория частичных алгебраических действий, будучи продолжением теории полных действий, пользуясь ее достижениями, связанная с ней идеями и опытом приложений за пределами алгебры, все же должна оформиться как самостоятельное направление в обширной области современной алгебры.
К настоящему времени опубликованы сотни работ, специально посвященных изучению частичных действий. Что касается работ, в которых те или иные частичные действия встречаются по ходу исследования, то число их не поддается оценке. О частичных действиях говорится и в некоторых общих алгебраических трудах, но всегда очень кратко.
Пока еще не было достаточно полного и связного изложения теории частичных алгебраических действий. Господствует разнобой в исходных понятиях и даже в обозначениях и терминологии. Недостает связей между отдельными работами. Дает себя знать недостаточность разработки отдельных вопросов, нужных для построения общей теории.
Частично упорядоченные множества
Бинарное отношение  на множестве А называется антисимметричным если:
на множестве А называется антисимметричным если:
 (
( 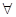 а,в
а,в  А) а τ в
А) а τ в  в τ а
в τ а
Бинарное отношение  на множестве А называется рефлексивным если:
на множестве А называется рефлексивным если:
( 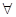 a
a  A) a
A) a  a
a
Бинарное отношение  на множестве А называется транзитивным если:
на множестве А называется транзитивным если:
( 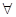 a ,в, c
a ,в, c  A) a
A) a  в
в  в
в  c → а
c → а  с
с 
Пример 1.
Отношение 
 делимости (нацело) на множестве натуральных чисел N антисимметрично. В самом деле, если а
делимости (нацело) на множестве натуральных чисел N антисимметрично. В самом деле, если а  в, в
в, в  а, то существуют натуральные q 1,q
а, то существуют натуральные q 1,q 
 N, такие, что а=в q 1, в=а q
N, такие, что а=в q 1, в=а q  откуда а=а q 1 q
откуда а=а q 1 q  , то есть q 1 q
, то есть q 1 q  =1. Но,
=1. Но,
q 1,q 
 N,следовательно q 1 = q
N,следовательно q 1 = q  =1, откуда следует, что а = в.
=1, откуда следует, что а = в.
Рефлексивное антисимметричное транзитивное бинарное отношение на множестве А называется отношением порядка (частичного порядка) на множестве А.
Множество А с заданным на нем отношением частичного порядка ≤ называют частично упорядоченным множеством и обозначают < А; ≤ >.
В дальнейшем для удобства будем пользоваться сокращением ЧУМ, обозначающим частично упорядоченное множество.
Пример 2.
< N, ≤ > − обычное нестрогое неравенство чисел (в школьном смысле). Нужно доказать транзитивность, рефлексивность и антисимметричность этого отношения ≤.
a) a ≤ a ,(2 ≤ 2) – рефлексивность,
b) если а ≤ в , в ≤ с, то a ≤ c , (3 ≤ 4, 4 ≤ 5 → 3 ≤ 5 ) – транзитивность,
c) если a ≤ в , в ≤ a , то a =в , (3 ≤ 3, 3 ≤ 3 → 3=3 ) – антисимметричность.
Из этого следует, что < N, ≤ > - ЧУМ.
Пример 3.
< N,  > .
> .
a) Отношение делимости  на множестве натуральных чисел N рефлексивно, т.к всякое число кратно самому себе, т.ет.к для любого а
на множестве натуральных чисел N рефлексивно, т.к всякое число кратно самому себе, т.ет.к для любого а  N всегда a = a∙1 (1
N всегда a = a∙1 (1  N), это , по смыслу отношение
N), это , по смыслу отношение  , имеем а
, имеем а  а . Следовательно,
а . Следовательно,  рефлексивно .
рефлексивно .
б) Если первое число делится нацело на второе(т.е кратное второму), а второе кратно третьему, то первое кратно третьему, значит отношение  транзитивно, т.е. если а
транзитивно, т.е. если а  в, в
в, в  с, a,в,c
с, a,в,c  N. Значит, существуют такие q
N. Значит, существуют такие q  ,q
,q 
 N, что
N, что
a = в q  ,
,
в = c q  ,
,
откуда
a = c (q  q
q  ).
).
Обозначим: q = q  q
q 
 N. Имеем
N. Имеем
a = cq,
где q  N, т.е. а
N, т.е. а  с – по определению
с – по определению  . Следовательно, отношение
. Следовательно, отношение  транзитивно.
транзитивно.
в) Антисимметричность отношения  следует из того, что два натуральных числа, кратных друг другу, равны между собой, т.е. если а
следует из того, что два натуральных числа, кратных друг другу, равны между собой, т.е. если а  в, в
в, в  а, то существуют такие q 1,q
а, то существуют такие q 1,q 
 N, что
N, что
а=в q 1,
в=а q  ,
,
откуда
а=а q 1 q  ,
,
то есть q 1 q  =1. Но, q 1,q
=1. Но, q 1,q 
 N,следовательно q 1 = q
N,следовательно q 1 = q  =1, откуда следует, что
=1, откуда следует, что  а = в. Следовательно
а = в. Следовательно  антисимметрично.
антисимметрично.
Поэтому  есть частичный порядок и , стало быть, < N,
есть частичный порядок и , стало быть, < N,  > - ЧУМ(частично упорядоченным множеством).
> - ЧУМ(частично упорядоченным множеством).
 Элементы a,в ЧУМа А называются несравнимыми изаписываются
Элементы a,в ЧУМа А называются несравнимыми изаписываются
 а||в , если a ≤ в и в ≤ а.
а||в , если a ≤ в и в ≤ а.
Элементы a,в ЧУМа А называются сравнимыми если a ≤ в или в ≤ а.
Частичный порядок ≤ на A называется линейным, а само ЧУМ линейно – упорядоченным илицепью, если любые два элемента из А сравнимы , т.е. для любых a,в  A, либо a ≤ в, либо в ≤ a.
A, либо a ≤ в, либо в ≤ a.
Пример 4.
< N, ≤ >, <R, ≤ > - являются цепью. Однако <В(М) ;  > ,где В(М) - множество всех подмножеств множества М или В(М) называется булеаном на множестве М, не является цепью , т.к. не для любых двух подмножеств множество М одно является подмножеством другого.
> ,где В(М) - множество всех подмножеств множества М или В(М) называется булеаном на множестве М, не является цепью , т.к. не для любых двух подмножеств множество М одно является подмножеством другого.
Пусть < А, ≤ > - произвольный ЧУМ.
Элемент m  A называется минимальным, если для любого x
A называется минимальным, если для любого x  A из того, что x ≤ m следует x = m.
A из того, что x ≤ m следует x = m.
Смысл этого понятия в том, что А не содержит элементов строго меньших этого элемента m. Говорят , что х строго меньше m и записывают х < m, если x ≤ m, но притом x ≠ m. Аналогично определяется максимальный элемент этого ЧУМ. Ясно, что если m 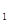 , m
, m  - разные минимальные (максимальные) элементы ЧУМ, то m
- разные минимальные (максимальные) элементы ЧУМ, то m  || m
|| m  .
.
В теории частично упорядоченных множеств условие a ≤ в иногда читают так: элемент а содержится в элементе в или элемент в содержит элемент а.
Лемма.
Каждый элемент конечного ЧУМа содержит минимальный элемент и содержится в максимальном элементе этого ЧУМа.
Доказательство:
Пусть а – произвольный элемент конечного ЧУМа S. Если а – минимальный элемент, то в силу рефлексивности, лемма доказана. Если А не минимален, то найдется элемент а  такой, что
такой, что
а  < а (1)
< а (1)
Если а  минимален, то всё доказано. Если же элемент а
минимален, то всё доказано. Если же элемент а  не является
не является
минимальным, то для некоторого а  получим
получим
а  < а
< а  (2)
(2)
Если а  минимален, то из (1), (2), благодаря транзитивности, заключаем, что а содержит минимальный элемент а
минимален, то из (1), (2), благодаря транзитивности, заключаем, что а содержит минимальный элемент а  . Если же а
. Если же а  не минимален, то
не минимален, то
а  < а
< а  (3)
(3)
для некоторого а 
 S. И так далее. Указанный процесс не может быть бесконечным в виду конечности самого множества S .
S. И так далее. Указанный процесс не может быть бесконечным в виду конечности самого множества S .
Таким образом, на некотором n – ом шаге рассуждений процесс оборвется, что равносильно тому, что элемент а  минимален. При этом
минимален. При этом
а  < а
< а 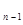 <
<  < а
< а  < а
< а  < а
< а
За счет транзитивности отсюда следует, что элемент а содержит минимальный элемент а  . Аналогично, элемент а содержится в максимальном элементе. Лемма доказана.
. Аналогично, элемент а содержится в максимальном элементе. Лемма доказана.
Следствие.
Конечное ЧУМ содержит, по меньшей мере, один минимальный элемент.
Сейчас мы введем важное для дальнейшего изложения понятие диаграммы конечного ЧУМа S .
Вначале берем все минимальные элементы m  , m
, m  ,
,  , m
, m  в S . Согласно следствию такие найдутся . Затем в частично упорядоченном множестве
в S . Согласно следствию такие найдутся . Затем в частично упорядоченном множестве
S  = S \ {m
= S \ {m  , m
, m  ,
,  , m
, m  },
},
которые , как и S , является конечным , берем минимальные элементы,
 ,
,  ,
,  ,
,  и рассматриваем множество
и рассматриваем множество
 = S
= S  \ {
\ {  ,
,  ,
,  ,
,  }
}
Элементы “ первого ряда “m  , m
, m  ,
,  , m
, m  изображаем точками. Несколько выше отмечаем точками элементы “ второго ряда”
изображаем точками. Несколько выше отмечаем точками элементы “ второго ряда”  ,
,  ,
,  ,
,  и соединяем отрезками точки
и соединяем отрезками точки  в том и только том случаи, если m
в том и только том случаи, если m  <
< 
Далее отыскиваем минимальные элементы ЧУМа  , изображаем их точками “третьего ряда” и соединяем точками “второго ряда” указанным выше способом. Продолжаем процесс до тех пор , пока не будут исчерпаны все элементы данного ЧУМа S . Процесс конечен в силу конечности множества S. Полученную совокупность точек и отрезков называют диаграммой ЧУМа S. При этом a < в тогда и только тогда, когда от “точки” а можно перейти к “точки” в по некоторой “восходящей” ломаной. В силу этого обстоятельства , любое конечное ЧУМ можно отождествить с его диаграммой.
, изображаем их точками “третьего ряда” и соединяем точками “второго ряда” указанным выше способом. Продолжаем процесс до тех пор , пока не будут исчерпаны все элементы данного ЧУМа S . Процесс конечен в силу конечности множества S. Полученную совокупность точек и отрезков называют диаграммой ЧУМа S. При этом a < в тогда и только тогда, когда от “точки” а можно перейти к “точки” в по некоторой “восходящей” ломаной. В силу этого обстоятельства , любое конечное ЧУМ можно отождествить с его диаграммой.
Пример 5.
|
|
 | ||||||
|
| |||||
Здесь задано диаграммой ЧУМ S = {m  , m
, m  ,
,  ,
,  ,
, 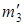 ,
,  },в которой m
},в которой m  <
<  , m
, m  <
<  , m
, m  <
<  m
m  <
<  , m
, m  <
<  m
m  <
<  , m
, m  <
< 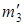 .
.
Элемент m называется наименьшим элементом ЧУМа, если для любого x  A всегда m ≤ x.
A всегда m ≤ x.
Понятно, что наименьший элемент является минимальным, но обратное не верно: не всякий минимальный элемент является наименьшим. Наименьший элемент (если такой имеется) только один. Аналогично определяется наибольший элемент.
Пример 6.
|
|
|
|
Это ЧУМ , элементы которого попарно несравнимы. Такие частично
упорядоченные множества называются антицепями.
Пример 7.

|
|
|
0
Эта цепь с наименьшим и наибольшим элементом. Где 0 - наименьший элемент , а 1 – наибольший элемент.
Пусть М – подмножество частичного упорядоченного множества А. Элемент а  A называют нижней гранью множества М, если а ≤ х для любого x
A называют нижней гранью множества М, если а ≤ х для любого x  М.
М.
Наибольшая из всех нижних граней множества М, если она существует, называется точной нижней гранью множества М и обозначают inf M.
Пусть < А, ≤ > - произвольный ЧУМ. Элемент с  A называется точной нижней гранью элементов a,в
A называется точной нижней гранью элементов a,в  A, если с = inf{a ,в}.
A, если с = inf{a ,в}.
Замечание 1.
Не во всяком ЧУМ для любых двух элементов существует точная нижняя грань.
Покажем это на примере.
Пример 8.

Для {a;c},{d;e} нет нижней грани,
inf{a;в}=d, inf{в;c}=e.
Пример 9.
|
 |
Приведем пример ЧУМ, у которого для любых элементов существует точная нижняя грань.
inf{a;в}=d, inf{a;d}=d, inf{a;0}=0, inf{a;c}=0, inf{a;e}=0,
inf{в;c}=e, inf{в;e}=e, inf{в;d}=d,
inf{c;e}=c, inf{c;0}=0, inf{c;d}=0,
inf{d;e}=0, inf{d;0}=0,
inf{e;0}=0.
Определение: Частично упорядоченное множество, в котором для любых двух элементов существует точная нижняя грань, называется полурешеткой.
Пример 10.
Приведем пример ЧУМ, которое не является полурешеткой.
Пусть < N, ≤ > - линейно - упорядоченное множество натуральных чисел и e  ,e
,e 
 N. На множестве N
N. На множестве N  = N
= N  { e
{ e  ,e
,e  } определим бинарное отношение ≤ , пологая что x ≤ y, если x , y
} определим бинарное отношение ≤ , пологая что x ≤ y, если x , y  N, где x ≤ y, или если x
N, где x ≤ y, или если x  N, y
N, y  { e
{ e  ,e
,e  }. Также считаем по определению : e
}. Также считаем по определению : e  ≤ e
≤ e  ,e
,e  ≤ e
≤ e  .
.
Диаграмма этого ЧУМ следующая:
|
|

Любое натуральное число n ≤ e  и n ≤ e
и n ≤ e  , но в N нет наибольшего элемента, следовательно, N
, но в N нет наибольшего элемента, следовательно, N  - ЧУМ, но не полурешетка.
- ЧУМ, но не полурешетка.
Итак, по самому определению, полурешетка есть модель (как множество с отношением ≤ ). Как мы сейчас увидим к понятию полурешетки возможен и другой подход, а именно, полурешетку можно определить как некоторую алгебру.
Для этого введем некоторые дополнительные алгебраические понятия. Как известно, полугруппой называется непустое множество с заданной на нем ассоциативной бинарной алгебраической операцией.
Произвольную полугруппу обычно обозначают S (semigroup).
Определение. Элемент e  S называется идемпотентом, если
S называется идемпотентом, если
e  = e , то есть e · e = e .
= e , то есть e · e = e .
Пример 11.
Полугруппа < N; · > − обладает единственным идемпотентом 1.
Полугруппа < Z; + > − обладает единственным идемпотентом 0.
Полугруппа < N; + > − не имеет идемпотента, т.к. 0  N.
N.
Для любого непустого множества X, как обычно, через 

 обозначается множество всех подмножеств множества X – булеан множества X.
обозначается множество всех подмножеств множества X – булеан множества X.
Полугруппа <В  ;
; 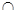 > - такова, что каждый ее элемент идемпотентен.
> - такова, что каждый ее элемент идемпотентен. 
A  В
В  , A = A
, A = A 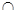 A .
A .
Полугруппа называется идемпотентной полугруппой или связкой, если каждый ее элемент является идемпотентным. Таким образом, примерами связки является всякий булеан относительно объединения.
Пример 12.
Пусть X – произвольное множество.
B  – множество всех подмножеств множества Х.
– множество всех подмножеств множества Х.
B  – называется булеаном на множестве Х.
– называется булеаном на множестве Х.
Если Х = {1,2,3} , то
B  = {Ø,{1},{2},{3},{1,2},{2,3},{1,3},{1,2,3}}.
= {Ø,{1},{2},{3},{1,2},{2,3},{1,3},{1,2,3}}.
Так как пересечение двух подмножеств множества Х вновь является подмножеством в Х, то имеем группоид < В  ;
; 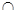 > , более того , это полугруппа и даже связка, так как А
> , более того , это полугруппа и даже связка, так как А  В
В  и А
и А  = А
= А 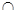 А =А.
А =А.
Точно также, имеем связку <; В 
 > .
> .
Коммутативная связка называется полурешеткой.
Пример 13.
Пусть Х = {1,2,3}, построим диаграмму < В  ;
;  >.
>.
|

Приведем примеры ЧУМ, но не полурешетки.
Пример 14.
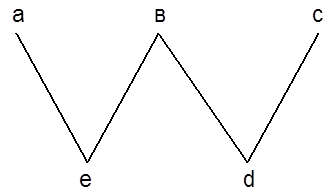 |
ЧУМ с двумя нижними гранями е и d , которые между собой не сравнимы: е||d. Следовательно, inf{a;с} не существует.
Пример 15.
 |
ЧУМ с двумя нижними гранями с и d, которые между собой несравнимы: с||d. Следовательно, inf{a;в} не существует.
Приведем примеры полурешеток.
Пример 16.
Диаграмма:
а

|
Является полурешеткой , т.к. для любых двух элементов существует точная нижняя грань, т.е.
inf{a;в}=в, inf{a;с}=с, inf{a;d}=d,
inf{в;c}=d, inf{в;d}=d,
inf{c;d}=d.
|
 |
|
|
Является полурешеткой , т.к. для любых двух элементов существует точная нижняя грань, т.е.
inf{a;в}=в, inf{a;с}=с, inf{в;c}=с.
Теорема 1.
Пусть <S ; ≤ > - полурешетка. Тогда <S ;  > коммутативная связка, где
> коммутативная связка, где
 a
a  в = inf {a,в} (*).
в = inf {a,в} (*).
Доказательство:
Нужно доказать, что в <S ;  > выполняются следующие тождества:
> выполняются следующие тождества:
(1) x  y = y
y = y  x
x
(2) (x  y)
y)  z = x
z = x  ( y
( y  z)
z)
(3) x  x = x
x = x
1) Согласно равенству(*)
x  y = inf (x,y) = inf (y,x) = y
y = inf (x,y) = inf (y,x) = y  x
x
2) Обозначим а = (x  y)
y)  z, в = x
z, в = x  ( y
( y  z)
z)
Докажем, что а = в.
Для этого достаточно доказать , что
а ≤ в (4)
в ≤ а (5) (в силу антисимметричности)
Обозначим
с = x  y , d = y
y , d = y  z
z
По смыслу, а точная нижняя грань между с и z
а ≤ с , а ≤ z , c ≤ x,следовательно, в силу транзитивности a ≤ x .
Аналогично, а ≤ y, т.е. а – общая нижняя грань для y и z . А d – их точная нижняя грань .
Следовательно, a ≤ d, но в = inf {x , d}.
Из неравенства a ≤ x , a ≤ d следует , что а – некоторая общая нижняя грань для х и d, а в – их точная нижняя грань, следовательно,
а ≤ в  (4) доказано.
(4) доказано.
Аналогично доказывается (5).
Из (4) и (5) , в виду антисимметричности, заключаем, что
а = в.
Этим мы доказали ассоциативность операции (  ).
).
3) Имеем x  х = inf {x,x} = x.
х = inf {x,x} = x.
Равенство выполняется за счет рефлексивности : х ≤ х.
Т.о. построенная алгебра <S ;  > будет коммутативной идемпотентной полугруппой , т.е. коммутативной связкой.
> будет коммутативной идемпотентной полугруппой , т.е. коммутативной связкой.
Теорема 2.
Пусть <S ; · > - коммутативная идемпотентная полугруппа, тогда бинарное отношение ≤ на S, определяемое равенство
≤ = {(a,в)  S × S | a ·в = а},
S × S | a ·в = а},
является частичным порядком. При этом ЧУМ <S ; ≤ > является полурешеткой .
Доказательство:
1) рефлексивность ≤.
По условию <S ; · > удовлетворяет трем тождествам:
(1) х  = х
= х
(2) х· y = y·x
(3) (x·y)·z = x·(y·z)
Тогда х·х = х  = х – в силу (1). Поэтому х ≤ х.
= х – в силу (1). Поэтому х ≤ х.
2) антисимметричность ≤ .
Пусть х ≤ у и у ≤ х, тогда по определению ,
(4) х·у = х
(5) у·х = у
отсюда, благодаря коммутативности, имеем х = у.
3) транзитивность ≤.
Пусть х≤ у и у ≤ z тогда , по определению,
(6) х·у = х
(7) у· z = у
Имеем x·z = (x · y)·z  x ·(y·z)
x ·(y·z)  х·у
х·у  х
х
Итак, x·z = x, то есть х ≤ z.
Таким образом, имеем ЧУМ <S ; ≤ >. Остается показать, что для любых (а, в) 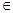 S существует inf{а,в}.
S существует inf{а,в}.
Берем произвольные а,в 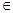 S и докажем, что элемент с = а·в является inf{а,в}, т.е с = inf{а,в}.
S и докажем, что элемент с = а·в является inf{а,в}, т.е с = inf{а,в}.
В самом деле ,
с·а = (а·в)·а 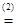 а·(а·в)
а·(а·в)  (а·а)·в
(а·а)·в  а·в = с,
а·в = с,
т.о. с ≤ а.
Аналогично, с·в = (а·в)·в  а·(в·в)
а·(в·в)  а·в = с,
а·в = с,
т.е. с ≤ в.
Итак, с – общая нижняя грань {а,в}.
Докажем ее точность.
Пусть d – некоторая общая нижняя грань для а и в:
(8) d ≤ a
(9) d ≤ в
Тогда
(10) d·a = d
(11) d· в = d
Поэтому
d · c = d ·(а·в)