 |
Главная |
Частичные группоиды и их свойства
|
из
5.00
|
Как известно, бинарная алгебраическая операция на множестве S – это отображение из декартового квадрата S×S. В этом случае говорят , что задано действие на S. Мы его в этом параграфе будем называть полным действием.
Всякое отображение из подмножества S×S в S называется частичным действием на S. Иными словами, частичное действие на S – это некоторая функция из S×S → S.
Можно сказать, что на S задано частичное действие (частичное умножение), если для любых элементов а,в  S произведение а·в либо не определено, либо определено однозначно. Попросту говоря, здесь не любые элементы перемножены.
S произведение а·в либо не определено, либо определено однозначно. Попросту говоря, здесь не любые элементы перемножены.
Множество S с заданным в нем частичным умножением называется частичным группоидом и обозначается (S ; · ) в отличие от полного группоида < S ; · >.
Если для полного группоида можно говорить о таблице Кэли, то для частичного группоида можно говорить о некотором аналоге таблицы Кэли, а именно о такой таблице, когда некоторые клетки пусты – это в том случае, когда произведение элементов неопределенно.
Пример 1. 
| • | a | в | с |
| а | a | в | с |
| в | ─ | в | ─ |
| с | в | а | ─ |
а·в= в, но в·а не определено, т.е. в·а = Ø . Символ “ Ø “ не принадлежит S , т.е. не является элементом из S. 
Пример 2.
Рассмотрим ЧУМ (S ; ≤ ).
 |
S = {a ,в, c , d}, где а ≤ а, в ≤ в, с ≤ с, d ≤ d, с ≤ а, с ≤ в, d ≤ а, d ≤ в.
В произвольном ЧУМе (S ; ≤ ) условимся обозначать:
а  в = inf{a ,в}.
в = inf{a ,в}.
Тогда указанное в примере ЧУМ относительно этого частичного действия  , является частичным группоидом (S ;
, является частичным группоидом (S ;  ), таблицей Кэли которого является следующая
), таблицей Кэли которого является следующая
| ^ | а | в | с | d |
| a | a | ─ | c | d |
| в | ─ | в | с | d |
| с | c | c | c | ─ |
| d | d | d | ─ | d |
В этом параграфе мы рассмотрим три вида ассоциативности: сильная ассоциативность, средняя ассоциативность, слабая ассоциативность.
Определение 1.
Частичный группоид (S ; · ) называется слабо ассоциативным, если
(  х ,y,z
х ,y,z 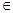 S) (x·y)·z
S) (x·y)·z  Ø
Ø  x·(y·z) → (x·y)·z = x·(y·z)
x·(y·z) → (x·y)·z = x·(y·z)  (*)
(*)
Определение 2.
Частичный группоид (S ; · ) называется средне ассоциативным, если
(  х ,y,z
х ,y,z 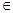 S) (x·y)·z
S) (x·y)·z  Ø
Ø  y·z → (x·y)·z = x·(y·z)
y·z → (x·y)·z = x·(y·z) 
Определение 3.
Частичный группоид (S ; · ) называется сильно ассоциативным, если
(  х ,y,z
х ,y,z  S) [(x·y)·z
S) [(x·y)·z  Ø
Ø  x·(y·z)
x·(y·z)  Ø → (x·y)·z = x·(y·z)]
Ø → (x·y)·z = x·(y·z)]  (*)
(*)
В сильно ассоциативном частичном группоиде выполняется свойства средней и слабой ассоциативности. Однако обратное отнюдь не обязательно.
Пример 3.
Дано А = {a ,в,с}. Зададим на А частичное действие умножение “ частичной таблицей Кэли”.
| • | a | в | с |
| а | ─ | ─ | ─ |
| в | с | ─ | ─ |
| с | ─ | в | с |
Получим некоторый частичный группоид. Проверим будет ли группоид сильно ассоциативным.
Пусть (x·y)·z  Ø т.к. х
Ø т.к. х  а, то либо х = с
а, то либо х = с  х = в
х = в
1) пусть х = с, тогда у = в  у = с
у = с
а) пусть у = в, тогда z = a
(с·в)·а  Ø
Ø  с·(в·а) определено
с·(в·а) определено
(с·в)·а = с·(в·а) равенство выполняется
б) пусть у = с, тогда z = в  z = с
z = с
а’) если z = в , тогда
(с·с)·в  Ø
Ø  с·(с·в) определено
с·(с·в) определено
(с·с)·в = с·(с·в) равенство выполняется
б’) если z = с, тогда
(с·с)·с  Ø
Ø  с·(с·с) определено
с·(с·с) определено
(с·с)·с = с·(с·с) равенство выполняется
2) пусть х = в, тогда у = а ,а z = в  z = c
z = c
а) если у = а и z = в
(в·а)·в  Ø= в·(а·в) не определено
Ø= в·(а·в) не определено
(в·а)·в  в·(а·в) равенство не выполняется
в·(а·в) равенство не выполняется
б) пусть у = а и z = с
(в·а)·с  Ø= в·(а·с) не определено
Ø= в·(а·с) не определено
(в·а)·с  в·(а·с) равенство не выполняется
в·(а·с) равенство не выполняется
Итак, по определению, частичный группоид не является сильно ассоциативным . Но это еще не означает, что (S ; · ) не является слабо ассоциативным.
Выясним это.
Пусть(x·y)·z  Ø
Ø  x·(y·z)
x·(y·z)  Ø .
Ø .
При х  а, у
а, у  а, а именно, когда
а, а именно, когда
х = в  х = с
х = с
у = в  у = с
у = с
этот частичный группоид является слабо ассоциативным.
Пример 4.
Пусть А = {a , в,с}, можно задать на А следующую таблицу Кэли. Получим некоторый частичный группоид. Проверим будет ли этот группоид средне ассоциативным.
| • | a | в | с |
| а | с | а | ─ |
| в | |||
| с | а | а | ─ |
Пусть (x·y)·z  Ø т.к. х
Ø т.к. х  в, тогда х = а
в, тогда х = а  х = с
х = с
1) пусть х = а, тогда у = а  у = в
у = в
а) пусть у = а, тогда z = a, z = в
а’) если z = а , тогда
(а·а)·а  Ø
Ø  а·a определено
а·a определено
(а·а)·а  а·(а·a) равенство не выполняется
а·(а·a) равенство не выполняется
б’) если z = в, тогда
(а·а)·в  Ø
Ø  а·в определено
а·в определено
(а·а)·в  а·(а·в) равенство не выполняется
а·(а·в) равенство не выполняется
Отсюда, мы видим, что группоид не является средне ассоциативным. Выясним является ли он слабо ассоциативный.
Пусть (x·y)·z  Ø
Ø  x·(y·z)
x·(y·z)  Ø, т.к. х
Ø, т.к. х  в, тогда х = а
в, тогда х = а  х = с
х = с
1) пусть х = а, тогда у = а  у = в
у = в
а) пусть у = а, тогда z = a, z = в
а’) если z = а , тогда
(а·а)·а  Ø= а·(а·a) не определено
Ø= а·(а·a) не определено
(а·а)·а  а·(а·a)
а·(а·a)
б’) если z = в, тогда
(а·а)·в  Ø
Ø  а·(а·в) определено
а·(а·в) определено
(а·а)·в = а·(а·в) равенство выполняется
б) пусть у = в, тогда z = a, z = в
а’) если z = а , тогда
(а·в)·а  Ø= а·(в·a) не определено
Ø= а·(в·a) не определено
(а·в)·а  а·(в·a)
а·(в·a)
б’) если z = в, тогда
(а·в)·в  Ø
Ø  а·(в·в) не определено
а·(в·в) не определено
(а·в)·в  а·(в·в) равенство не выполняется
а·(в·в) равенство не выполняется
2) пусть х = с, тогда у = а , у = в
а) пусть у = а, тогда z = a, z = в
а’) если z = а , тогда
(с·а)·а  Ø= с·(а·a) не определено
Ø= с·(а·a) не определено
(с·а)·а  с·(а·a) равенство не выполняется
с·(а·a) равенство не выполняется
б’) если z = в, тогда
(с·а)·в  Ø
Ø  с·(а·в) определено
с·(а·в) определено
(с·а)·в = с·(а·в) равенство выполняется
Итак , мы видим что частичный группоид является слабо ассоциативным при х = а и z = в или при х = с если у = а и z = в.
Определение 4.
Частичный группоид (S ; · ) называется коммутативным, если
(  х, y
х, y 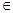 S) x·y = y·х
S) x·y = y·х 
Определение 5.
Частичный группоид (S ; · ) называется катенарным, если
(  х ,y,z
х ,y,z  S) (x·y
S) (x·y  Ø
Ø  y·z) → [(x·y)·z
y·z) → [(x·y)·z  Ø
Ø  x·(y·z)]
x·(y·z)]
Определение 6.
Частичный группоид (S ; · ) называется идемпотентным, если
(  х
х  S) х
S) х 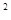 = х
= х
Приведем пример некатенарного частичного группоида.
Пример 5.
| ^ | а | в | с | d |
| a | a | ─ | c | d |
| в | ─ | в | с | d |
| с | c | c | c | ─ |
| d | d | d | ─ | d |
Имеем с  а = с
а = с  Ø, а
Ø, а  d = d
d = d  Ø. Однако, (с
Ø. Однако, (с  а)
а)  d = c
d = c  d
d  Ø. Следовательно, заданный ЧГ не является катенарным.
Ø. Следовательно, заданный ЧГ не является катенарным.
Ясно, что понимаем под термином “ общая верхняя грань” элементов а и в некоторого ЧУМ.
Определение 7.
ЧУМ называется категорийным, если любые два его элемента, имеющие верхнюю грань, имеют точную нижнюю грань.
Пример 6.
 |
Чум не является категорийным, т.к. элементы с и d имеют верхнюю грань , но не имеют точную нижнюю грань.
Пример 7.
Частично упорядоченное множество, задаваемое таблицей Кэли:
| а | в | с | d | e | f | g | h | k | s | |
| a | a | в | c | d | h | g | g | h | | |
| в | в | в | d | d | 0 | g | g | 0 | | |
| c | c | d | c | d | h | 0 | 0 | h | | |
| d | d | d | d | d | 0 | 0 | 0 | 0 | | |
| e | h | 0 | h | 0 | e | 0 | 0 | h | | |
| f | g | 0 | 0 | 0 | 0 | f | g | 0 | | |
| g | G | g | 0 | 0 | 0 | g | g | 0 | | |
| h | h | 0 | h | 0 | h | 0 | 0 | h | | |
| k | | | | | | | | | k | s |
| s | | | | | | | | | s | s |

является категорийным, так как любые два его элемента, имеющие верхнюю грань, имеют точную нижнюю грань.
Пример 8.
Частично упорядоченное множество


имеющее следующую таблицу Кэли:
| • | а | в | с | d | f |
| а | а | с | с | - | - |
| в | с | в | с | - | - |
| с | с | с | с | - | - |
| d | - | - | - | d | f |
| f | - | - | - | f | f |
является категорийным, так как любые два его элемента, имеющие верхнюю грань, имеют точную нижнюю грань.
Понятно, что всякая полурешетка – это категорийное ЧУМ (но не на оборот), т.к. любые два элемента имеют точную нижнюю грань. Иными словами, класс всех категорийных ЧУМ содержит класс всех полурешеток, но с ним не совпадает. Т.о. любое предложение, доказанное для категорийных ЧУМ влечет в качестве очевидного следствия некоторую теорему относительно полурешеток.
Приведем примеры полурешеток.
|
Диаграмма:
 |
|
называется диамантом, и определяется полурешеткой, имеющей следующую таблицу Кэли:
| ^ | а | в | с | d |
| a | a | в | c | d |
| в | в | в | d | d |
| с | c | d | c | d |
| d | d | d | d | d |
|
|
 Диаграмма:
Диаграмма:
|
| ||||||
| |||||||
называется пентагоном, и определяется полурешеткой, имеющей следующую таблицу Кэли:
| • | а | в | с | е | 0 |
| а | а | 0 | 0 | а | 0 |
| в | 0 | в | с | в | 0 |
| с | 0 | с | с | с | 0 |
| е | а | в | с | е | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 |
Пример 11.
Полурешетка, задаваемая таблицей Кэли:
| • | а | в | с | е | 0 |
| а | а | 0 | 0 | а | 0 |
| в | 0 | в | 0 | в | 0 |
| с | 0 | 0 | с | с | 0 |
| е | а | в | с | е | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 |
имеет диаграмму:
|


|  |
| |||||
| |||||||
Теорема 1.
Пусть (S ; ≤ ) – категорийное ЧУМ, тогда (S ;  ) – катенарный идемпотентный коммутативный слабо ассоциативный частичный группоид.
) – катенарный идемпотентный коммутативный слабо ассоциативный частичный группоид.
Доказательство:
Для любого а  S всегда
S всегда
а  а = inf{a , a} = a поэтому частичный группоид S идемпотентен.
а = inf{a , a} = a поэтому частичный группоид S идемпотентен.
Имеем а  в = inf{a ,в} = inf{в, a} = в
в = inf{a ,в} = inf{в, a} = в  а , а поэтому S коммутативен.
а , а поэтому S коммутативен.
Проверим слабую ассоциативность.
Пусть (а  в)
в)  с
с  Ø
Ø  а
а  (в
(в  с) , обозначим
с) , обозначим
а  в = d, в
в = d, в  с = e, (а
с = e, (а  в)
в)  с = d
с = d  с = f, а
с = f, а  (в
(в  с) = а
с) = а  е = g
е = g
Докажем, что f = g.
По определению имеем f ≤ d ≤ a  f ≤ a,
f ≤ a,
f ≤ d ≤ в  f ≤ в (1)
f ≤ в (1)
f ≤ c (2)
Т.к. е = inf{в,с}, то из (1), (2) следует, что f ≤ e. Т.о. f – некоторая общая нижняя грань для а и е, а g – их точная нижняя грань, поэтому
f ≤ g (3)
Аналогично,
g ≤ f (4)
Неравенство (3), (4) и антисимметричность отношения ≤ обеспечивают f = g. Слабая ассоциативность доказана.
Проверим катенарность S .
Пусть а  в
в  Ø
Ø  в
в  с , обозначим а
с , обозначим а  в = х , в
в = х , в  с = y, отсюда х ≤ в, у ≤ в, т.е.
с = y, отсюда х ≤ в, у ≤ в, т.е.
в – общая верхняя грань х и у. Т.к. ЧУМ S категорийно, то существует inf{х,у}, т.е. существует в S х  у. Обозначим х
у. Обозначим х  у = z, покажем ,что
у = z, покажем ,что
а  (в
(в  с) = х
с) = х  с = z. Имеем z ≤ x, z ≤ y (т.к. z = inf{х,у}), y ≤ z
с = z. Имеем z ≤ x, z ≤ y (т.к. z = inf{х,у}), y ≤ z  z ≤ x , z ≤ c,
z ≤ x , z ≤ c,
z – нижняя грань для х и с.
Обеспечим точность.
Пусть t ≤ x , t ≤ c ( t – какая – либо нижняя грань ), т.к. t ≤ x , то t ≤ a, t ≤ в, по условию t ≤ с, т. е. t – общая нижняя грань для в и с. Отсюда следует по определению у , t ≤ y .
Итак, t ≤ x, t ≤ у следовательно t ≤ z (по определению z).
Катенарность доказана.
Теорема 2.
Если (S ; ·) – катенарный идемпотентный коммутативный слабо ассоциативный частичный группоид, то отношение
≤ = { (а,в)  S×S | ав = а
S×S | ав = а  } (2)
} (2)
Является отношением порядка. При этом ЧУМ <S ; ≤ > – является катенарным.
Доказательство:
Докажем рефлексивность отношения ≤ . Т.к. частичный группоид S идемпотентен , то a · a = a отсюда , по определению (2) а ≤ а.
Проверим антисимметричность.
Если а ≤ в , в ≤ а ,то а·в = а, в·а = в, левые части равны в виду коммутативности , значит равны и правые, следовательно а = в.
Осталось доказать транзитивность.
Пусть а ≤ в , в ≤ с, тогда а·в = а, в·с = в, а·с = (а·в)·с. В силу катенарности имеем (а·в)·с  Ø , а·(в·с)
Ø , а·(в·с)  Ø , отсюда в силу слабой ассоциативности
Ø , отсюда в силу слабой ассоциативности
(а·в)·с = а·(в·с), а поэтому, а·с = а·(в·с) = а·в = а.
Итак, а·с = а, т.е. а ≤ с.
Т.о. имеем ЧУМ <S ; ≤ > .
Проверим категоричность ЧУМ.
Пусть z – общая верхняя грань для х и у. Следовательно, х ≤ z, y ≤ z , отсюда х· z = x , y · z = y, тогда z · y = y. В силу катенарности (x·y)·z  Ø
Ø  x·y
x·y  Ø.
Ø.
Обозначим х·у = s, докажем , что s точная нижняя грань .
Имеем s · x = (x·y)·x = x ·(x · y) = (x · x)·y = x · y = s (в виду катенарности и слабой ассоциативности), следовательно, s ≤ x, т.е. s – общая нижняя грань.
Из этих теорем вытекают известные в теории полурешеток два следствия.
Следствие 1.
Если <S ; · > - идемпотентная коммутативная полугруппа, то отношение ≤ , определенное равенством (2), является частичным порядком. При этом для любых двух элементов в S существует точная нижняя грань.
Следствие 2.
Если <S ; · > - частично упорядоченное множество, в котором любых двух элементов существует точная нижняя грань, то относительно операции
а  в = inf{a ,в} (3)
в = inf{a ,в} (3)
множество S является идемпотентной коммутативной полугруппой.
ЗАКЛЮЧЕНИЕ
В заключении можно отметить, что теорию упорядоченных множеств создал Г. Кантор. В 1883 он ввёл понятие вполне упорядоченного множества и порядкового числа, а в 1895 – понятие упорядоченного множества и порядкового типа. В 1906–07 С. О. Шатуновский сформулировал определения направленного множества (у Шатуновского – расположенный комплекс) и предела по направленному множеству (амер. математиками Э. Г. Муром и Г. Л. Смитом эти же понятия были рассмотрены независимо от Шатуновского, но значительно позднее – в 1922). Общее понятие частично упорядоченного множества принадлежит Ф. Хаусдорфу (1914).
Таким образом, теория частичных алгебраических действий, будучи продолжением теории полных действий, пользуясь ее достижениями, связанная с ней идеями и опытом приложений за пределами алгебры, все же должна оформиться как самостоятельное направление в обширной области современной алгебры.
К настоящему времени опубликованы сотни работ, специально посвященных изучению частичных действий. Что касается работ, в которых те или иные частичные действия встречаются по ходу исследования, то число их не поддается оценке. О частичных действиях говорится и в некоторых общих алгебраических трудах, но всегда очень кратко.
Список литературы
1. А.К. Клифорд, Г. Престон. Алгебраическая теория полугрупп. 1972.
2. Грейцер. Общая теория решеток.Москва.-284с.
3. Кожевников О.Б. Частично упорядоченные множества частичных группоидов.Москва,1998. – 680с.
4. Е.С. Ляпин. Полугруппы. Москва: физмат, 1960.- 354с.
5. Ляпин Е.С. Алгебра и теория чисел. Москва, 1980.-589с.
|
из
5.00
|
Обсуждение в статье: Частичные группоиды и их свойства |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

