Возможности статистического подхода при выявлении своеобразных профилей развития творческих способностей

Мною рассмотрен метод, предложенный профессором Орловым А.И., который является профессором кафедры "Экономика и организация производства" факультета "Инженерный бизнес и менеджмент" Московского государственного технического университета им. Н.Э.Баумана.

Этот метод позволяет определить экстремальные, нетипичные значения выборок с точки зрения параллельного рассмотрения двух параметров.

В прикладной математической статистике часто рассматривают вероятностную модель двух независимых выборок числовых результатов наблюдений. Первая выборка описывается набором m случайных величин X1, X2, ... , Xm, имеющих одну и ту же функцию распределения F(x), а вторая выборка – набором n случайных величин Y1, Y2, ... , Yn, имеющих одну и ту же функцию распределения G(x), причем все эти m+n случайных величин X1, X2, ... , Xm, Y1, Y2, ... , Yn независимы в совокупности. Без ограничения общности можно считать, что m # n, в противном случае выборки можно поменять местами.  Обычно предполагается, что функции F(x) и G(x) непрерывны и строго возрастают. Из непрерывности этих функций следует, что с вероятностью единица все m+n результатов наблюдений различны. В реальных статистических данных иногда встречаются совпадения, но сам факт их наличия – свидетельство нарушений предпосылок только что описанной базовой математической модели.

Статистика S двухвыборочного критерия Вилкоксона определяется следующим образом. Все элементы объединенной выборки X1, X2, ..., Xm, Y1, Y2, ... , Yn упорядочиваются в порядке возрастания. Элементы первой выборки X1, X2, ..., Xm занимают в общем вариационном ряду места с номерами R1, R2, ..., Rm, другими словами, имеют ранги R1, R2, ..., Rm . Тогда

                                                           S = R1 + R2 + ... + Rm .                                                      

Статистика U Манна-Уитни определяется как число пар (Xi, Yj) таких, что Xi < Yj , среди всех mn пар, в которых первый элемент – из первой выборки, а второй – из второй. Как известно,

                                                           U = mn + m(m+1)/2 – S .                                                      

Поскольку S и U линейно связаны, то часто говорят о критерии Вилкоксона (Манна-Уитни). Не будем обсуждать здесь вопросы истории и терминологии, относящиеся к S и U.

Критерий Вилкоксона – один из самых известных инструментов непараметрической статистики (наряду со статистиками типа Холмогорова-Смирнова и коэффициентами ранговой корреляции). Свойствам этого критерия и таблицам его критических значений уделяется место во многих монографиях по математической и прикладной статистике.

Однако в литературе имеются и неточные утверждения относительно возможностей критерия Вилкоксона. Так, одни полагают, что с его помощью можно обнаружить различие между функциями распределения F(x) и G(x). По мнению других, этот критерий нацелен на проверку равенства медиан распределений, соответствующих выборкам. И то, и другое, строго говоря, неверно. Настоящая статья написана, чтобы внести ясность в рассматриваемый вопрос.

Ссылки на публикации с неточными и ошибочными утверждениями не приводим по нескольким причинам. Во-первых, таких публикаций слишком много. Во-вторых, некоторые из них после исключения ошибок представляют ценность для практически работающего статистика. В-третьих, зачем создавать рекламу плохим книгам. И т.п.

Введем некоторые обозначения. Пусть F-1(t) – функция, обратная к функции распределения F(x). Она определена на отрезке [0;1]. Положим L(t) = G(F-1(t)). Поскольку F(x) непрерывна и строго возрастает, то F-1(t) и L(t) обладают теми же свойствами. Важную роль в дальнейшем изложении будет играть величина a = P(X < Y) . Как нетрудно показать,

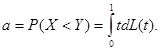
Введем также

                           (1)

Тогда математические ожидания и дисперсии статистик Вилкоксона и Манна-Уитни выражаются через введенные величины:

                        E(U) = mna , E(S) = mn + m(m+1)/2 – E(U) = mn(1- a) + m(m+1)/2,             

                                   D(S) = D(U) = mn [(n – 1) b2  + (m – 1) g2 + a(1 -a)].                (2)

Когда объемы обеих выборок безгранично растут, распределения статистик Вилкоксона и Манна-Уитни являются асимптотически нормальными с параметрами, задаваемыми формулами (1) .  

Если выборки полностью однородны, т.е. их функции распределения совпадают, справедлива гипотеза

                                                        H0: F(x) = G(x) при всех x,                                      (3)

то L(t) = t и a= 1/2. Подставляя в формулы (3), получаем, что

                                          E(S) = m(m+n+1)/2, D(S) = mn(m+n+1)/ 12.                                   

Следовательно, распределение нормированной и центрированной статистики Вилкоксона:

                                          T = ( S – m(m+n+1)/2) (mn(m+n+1)/ 12 ) – 1/2 ,                                    

при росте объемов выборок приближается к стандартному нормальному распределению (с математическим ожиданием 0 и дисперсией 1).

Из асимптотической нормальности статистики Т следует, что правило принятия решения для критерия Вилкоксона выглядит так:

- если |T| < то гипотеза (2) однородности (тождества) функций распределений принимается на уровне значимости a,

- если же |T| > то гипотеза (1) однородности (тождества) функций распределений отклоняется на уровне значимости .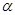

В прикладной статистике наиболее часто применяется уровень значимости  Тогда значение модуля статистики Т Вилкоксона надо сравнивать с граничным значением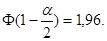

Правила принятия решений и таблица критических значений для критерия Вилкоксона строятся в предположении справедливости гипотезы полной однородности, описываемой формулой (1). А что будет, если эта гипотеза неверна? Другими словами, какова мощность критерия Вилкоксона?

Пусть объемы выборок достаточно велики, так что можно пользоваться асимптотической нормальностью статистики Вилкоксона. Тогда в соответствии с формулами (1) статистика T будет асимптотически нормальна с параметрами

                                            E(T) = ( 12mn ) 1/2 (1/2 – a) (m+n+1) – 1/2,                                      

                               D(T) = 12 [(n – 1) b2  + (m – 1) g2 + a(1 -a) ] (m+n+1) – 1.                        

Из формул (11) видно большое значение гипотезы

                                                          H01: a = P(X < Y) = 1/2 .                                                   

Если эта гипотеза неверна, то, поскольку m < n, справедлива оценка

                                               |M(T)| > (12m n (2n+1) – 1) 1/2 |1/2 – a ,                                 (4)

а потому |M(T)| безгранично растет при росте объемов выборок. В то же время, поскольку

то

                                    D(T) < 12 [(n – 1) + (m – 1) + 1/4] (m+n+1) – 1 <12.                               

Следовательно, вероятность отклонения гипотезы H01 , когда она неверна, т.е. мощность критерия Вилкоксона как критерия проверки гипотезы (4), стремится к единице при возрастании объемов выборок, т.е. критерий Вилкоксона является состоятельным для этой гипотезы при альтернативе

                                                       АH01:  a = P(X < Y) ё 1/2 .                                        (5)

Если же гипотеза (8) верна, то статистика T асимптотически нормальна с математическим ожиданием 0 и дисперсией, определяемой формулой

                                  D(T) = 12 [(n – 1) b2  + (m – 1) g2 + 1/4 ] (m+n+1) – 1.                  (6)

Гипотеза (4) является сложной, дисперсия (6), как показывают приводимые ниже примеры, в зависимости от значений b2 и g2 может быть как больше единицы, так и меньше единицы, но согласно неравенству (5) никогда не превосходит 12.

Приведем пример двух функций распределения F(x) и G(x) таких, что гипотеза (4) выполнена, а гипотеза (2) – нет. Поскольку

                                                         a = P(X < Y) = _ò F(x)dG(x) ,

1 – a = P(Y < X) = _ò G(x)dF(x),

и a = 1/2 в случае справедливости гипотезы (4), то для выполнения условия (3) необходимо и достаточно, чтобы

                                                                                  _ò (F(x) – G(x)) dF(x) = 0 ,                                              (7)

а потому естественно в качестве F(x) рассмотреть функцию равномерного распределения на интервале (-1; 1). Тогда формула (11) переходит в условие

                                                   _ò ( F ( x ) – G ( x )) dF ( x ) = – 1/2 _ò ( G ( x ) – ( x + 1)/2 ) dx = 0.                               

Это условие выполняется, если функция (G(x) – (x + 1)/2) является нечетной.

При проверке гипотезы однородности мы рассмотрели различные виды нулевых и альтернативных гипотез – гипотезу (2) и ее отрицание в качестве альтернативы, гипотезу (3) и ее отрицание, гипотезы о равенстве или различии медиан. В теоретических работах по математической статистике любят гипотезу сдвига, в которой альтернативой гипотезе (2) является гипотеза

                        H1: F(x) = G(x + r) при всех x и некотором r, отличным от нуля                  

Если верна альтернативная гипотеза H1, то вероятность P(X < Y) отлична от 1/2, и критерий Вилкоксона является состоятельным.

В некоторых прикладных постановках гипотеза (4) представляется естественной. Например, если одним и тем же прибором проводятся две серии измерений двух значений некоторой величины (физической, химической и т.п.). При этом функция распределения G(x) описывает погрешности измерения одного значения, а G(x+r) – другого. Однако в большинстве прикладных постановок нет никаких оснований считать, что отсутствие однородности всегда выражается столь однозначным образом, как следует из формулы (7). Поэтому мы, рассматривая проблему выбора статистического критерия для проверки однородности, пришли к выводу о необходимости использования критериев, состоятельных против любого отклонения от гипотезы однородности (4), прежде всего критериев Смирнова и типа омега-квадрат (Лемана-Розенблатта).

Отметим еще одно обстоятельство. Часто говорят (в соответствии с классическим подходом математической статистики), что нельзя проверять нулевые гипотезы без рассмотрения альтернативных. Однако при практическом анализе данных зачастую полностью ясна формулировка той гипотезы, которую желательно проверить (например, гипотезы полной однородности – см. формулу (3)), в то время как формулировка альтернативной гипотезы не очевидна (то ли это гипотеза о неверности равенства (3) хотя бы для одного значения x, то ли это альтернатива (4), то ли – альтернатива сдвига (5), и т.д.). В таких случаях целесообразно "обернуть" задачу – исходя из статистического критерия найти альтернативы, относительно которых он состоятелен. Именно это и проделано в настоящей статье для критерия Вилкоксона.