Для чего нужны быстрые алгоритмы?

Московский государственный университет им М.В. Ломоносова

Мехманико - математический факультет

Кафедра математической логики и теории алгоритмов

Наливайко Павел Владимирович

«История изучения теории потоков в сетях»

Реферат по истории математики

Научный руководитель: проф. Верещагин Н.К.

                                       

                                                                                       ____________________

Ведущий семинары: к.ф.н. Катречко С.Л.

                                                                                       ____________________

Москва, 2008

Оглавление

Введение.	3
Для чего нужны быстрые алгоритмы?	4
Глава 1. История изучения теории потоков · Начало исследований · Эвристика Болдырева · Отчет Харриса-Росса · Метод Форда-Фалекрсона · Алгоритм Эдмондса-Карпа · Дальнейшие улучшения алгоритма построения максимального потока · Хронологическая таблица результатов	6
Глава 2. Теория паросочетаний · Паросочетание в двудольном графе · Теорема Фробениуса · Теоремы Менгера и Кёнига · Связь между потоками и паросочетаниями	13
Глава 3. Задача о назначениях: «взвешенный» вариант задачи о паросочетаниях · Монж: оптимальное назначение · Теорема Эгервари · 1940е годы · Ранние 1950е · Вычислительные результаты начала 1950х · Венгерский метод Куна-Манкреша	16
Глава 4. Дальнейшие исследования в теории потоков · Потоки минимальной стоимости · Динамические потоки. Задача транспортировки · Универсально-максимальные динамические потоки · Наибыстрейшие потоки	21
Заключение	25
Библиография	26

Введение

Теория потоков в сетях – одно из современных направлений развития компьютерных наук в целом, и теории графов в частности. Многие комбинаторные задачи и линейные программы могут быть сформулированы и эффективно решены в терминах потоков.

 

Сеть представляет собой специальный вид графа. Сеть состоит из вершин и ребер. В практических задачах каждая вершина сети соответствует фабрике, складу, компьютеру, географическому или какому-либо другому объекту. Ребро соединяет пару вершин, в соответствии с дорогами, кабелями или другими каналами связи. В теории потоков, каждое ребро имеет пропускную способность, которая ограничивает количество информации (грузов, товаров...) которое может быть одновременно переправлено по этому ребру. В сети также выделены терминальные вершины. Они могут быть двух типов – источники и стоки.

 

Наглядно сеть можно представить себе как разветвленный трубопровод. Вершинами будут начала (источники) и концы (стоки) трубопровода, а также промежуточные узловые точки. Ребрами – трубы. Поток в сети соответствует жидкости, перемещаемой по трубопроводу.

 

Рис. 1. Поток в сети. Иллюстрация из Wikipedia.

 

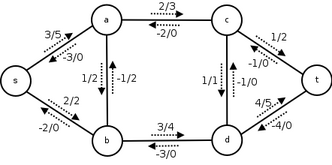
Поток в сети, с формальной точки зрения, это неотрицательная вещественнозначная функция, определенная на ребрах сети, обладающая дополнительными условиями консервативности (для каждой нетерминальной вершины сумма потока по входящим ребрам равна сумме потока по исходящим) и подчиненности пропускным способностей (поток по ребру не превышает его пропускной способности).

Первая, и самая естественная задача теории потоков – это организовать поток так, чтобы доставлять наибольшее количество потока из источника в сток. Эта задача получила название задачи о максимальном потоке.

 

С потоками в сетях тесно связана задача о паросочетании в двудольном графе. Эта задача возникла раньше, однако, является частным случаем задачи о максимальном потоке.

 

Далее в данной работе мы проследим за развитием исследований в этих областях. Мы постараемся понять, какие были мотивы у ученых для поиска решений этих задач.

 

Основные источники данной работы являются англоязычными. Более того, для многих терминов в русскоязычной литературе даже нет устоявшегося перевода. В таких случаях мы будем в скобках указывать англоязычный термин.

 

Для чего нужны быстрые алгоритмы?

Эффективность алгоритма принято измерять асимптотической оценкой времени работы алгоритма в зависимости от параметров исходной сети. (Употребляется также термин «сложность алгоритма» - «complexity» в англоязычной литературе.) Основным параметром является число вершин исходной сети (так как число ребер в большинстве практических задач не превосходит квадрата числа вершин). Алгоритмы, время работы которых не превосходит некоторого полинома от размера исходной сети (числа вершин), называются полиномиальными. Как правило, полиномиальные алгоритмы возможно эффективно реализовать на практике. Напротив, алгоритмы, так или иначе использующие перебор большого числа вариантов, по своей сложности обычно бывают экспоненциальными.

 

Начнем с рассмотрения простого примера, наглядно иллюстрирующего пользу теоретических исследований в области компьютерных наук. Пусть в памяти компьютера имеется N целых чисел, и необходимо расположить их в порядке возрастания. (Данная задача называется задачей сортировки). Рассмотрим следующий алгоритм: выберем среди данных чисел наименьшее, поставим его на первое место. Затем из оставшихся чисел снова выберем наименьшее, и поставим его на второе место. И так далее. Очевидно, что данный алгоритм решает задачу сортировки. Но насколько он эффективен? Несложно показать, что данному алгоритму требуется порядка N^2 действий. (Данная оценка называется асимптотикой работы алгоритма, и с помощью O-символики данный факт записывается так: сложность алгоритма есть O(N^2) ).

 

Предположим что N = 10^8. Современный однопроцессорный компьютер способен выполнять порядка ста миллионов элементарных операций (присваивание, сложение, вычитание...) в секунду. Таким образом, для сортировки данного набора чисел потребуется порядка (10^8)^2 / 10^8 = 100 миллионов секунд, или около трех лет.

 

В то же время, известны алгоритмы решения задачи сортировки со сложность O(NlogN). Самые известные из них – это алгоритм пирамидальной сортировки (heap sort) и «быстрая» (quick sort) сортировка Хоара (последняя, впрочем, имеет лишь время работы O(NlogN) «в среднем»). При N = 10^8 время работы таких алгоритмов получается около 30 секунд!

 

На примере данной задачи видно, что дополнительные исследования в алгоритмической области могут сократить объемы вычислений на порядки, за считанные секунды решить задачу, которая ранее с практической точки зрения казалась неразрешимой.