Глава 1. Общие сведения о задачах на экстремум. Примеры экстремальных задач

Оглавление

Введение

Глава 1. Общие сведения о задачах на экстремум. Примеры экстремальных задач

1. Общие свойства выпуклых фигур

1.1 Задачи

1.2 Решения

2. Изопериметрическая задача

2.1 Задачи

2.2 Решения

3. Задачи на максимум и минимум

3.1 Задачи

3.2 Решения

Глава 2. Оценка периметра пятиугольника единичного диаметра

1. Доказательство равенства четырех диагоналей пятиугольника единице

2. Отыскание оптимального пятиугольника

Заключение

Библиография

Введение

В жизни постоянно приходиться сталкиваться с необходимостью принять наилучшее возможное (оптимальное) решение. При этом часто случается так, что полезно прибегнуть к математике.

Оба понятия максимум и минимум объединяются одним термином "экстремум", что по латыни означает "крайнее". Задачи отыскания максимума и минимума называются экстремальными задачами.

Экстремальными задачами человек интересовался с античных времен. Уже в Древней Греции знали об экстремальных свойствах круга и шара: среди плоских фигур с одинаковым периметром наибольшую площадь имеет круг (решение изопериметрической задачи); шар имеет максимальный объем среди пространственных фигур с одинаковой площадью поверхности (решение изопифанной задачи). [4, 4]

История сохранила легенду о следующей самой древней экстремальной задаче, известной как задача Дидоны: указать форму границы участка, имеющей заданную длину, при которой площадь участка максимальна. Считается, что история этой задачи началась в IX веке до н.э., когда, как написал в своей поэме "Энеида" древнеримский поэт Вергилий, царевне Дидоне пришлось решать изопериметрическую задачу. Если знать экстремальное свойство круга, то решение получается немедленно: граница участка представляет часть окружности, имеющей заданную длину. Согласно легенде Дидона справилась с поставленной задачей и на месте отгороженного участка основала город Карфаген. Говорят, что старая крепость Карфагена действительно имела форму круга. [3, 29]

Экстремальными задачами занимались многие античные ученые (Евклид, Архимед, Аристотель и др.). В началах Евклида – первой научной монографии и первом учебном пособии в истории человечества, в труде вышедшем в IV веке до н.э. имеется задача на максимум. В современной редакции она выглядит так: вданный треугольник АВС вписать параллелограмм ADEF, наибольшей площади.Нетрудно показать, что решением этой задачи является параллелограмм, вершины D, E, F которого делят соответствующие стороны треугольника пополам. [4, 30]

Известна также задача античного математика Герона Александрийского, с которой мы знакомимся еще в школе: даны две точки А и В по одну сторону от прямой l. Требуется найти на прямой l такую точку D, что бы сумма расстояний от А до D и от В до D была наименьшей. Книга, где была изложена эта задача, называется "О зеркалах". Время написания этой книги неизвестно, но большинство исследователей считают, что она написана в I веке до н.э. При этом сам труд Герона не сохранился, и о нем известно из комментариев к нему написанных позже.

После гибели античной цивилизации научная жизнь в Европе стала возрождаться только в XV веке. Экстремальные задачи оказались среди тех, которыми интересовались лучшие умы того времени. [4, 7]

Задачи на экстремумы актуальны и в настоящее время, так как имеется много нерешенных задач на наибольшее и наименьшее значение некоторых величин, связанных с выпуклой фигурой. Так, например, до сих пор не решены следующие задачи: найти минимальную площадь S выпуклой фигуры, если известен диаметр D и ширина 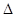 этой фигуры, причем 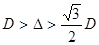; найти минимальную площадь выпуклой фигуры, если известна ширина и периметр фигуры. [8, 89]

Основная цель данной работы состоит в рассмотрении различных геометрических задач на максимум и минимум, а также в детальном разборе и доказательстве теоремы о пятиугольнике наибольшего периметра единичного диаметра.

Данная работа содержит две главы. Глава 1 состоит из трех параграфов. Каждый параграф построен следующим образом: сначала приводятся основные теоретические сведения, а затем рассматриваются задачи с дальнейшим их решением.

В 1 рассмотрены основные свойства выпуклых фигур. Данный параграф имеет вводный характер и в нем сосредоточены основные определения, используемые в дальнейшем, и приведены простейшие задачи, иллюстрирующие эти определения. Изучение представленных задач, позволяет более детально ознакомиться с определениями выпуклой фигуры, выпуклой кривой, опорной прямой выпуклой фигуры, обыкновенной и угловой точек выпуклой кривой, длины выпуклой кривой и площади выпуклой фигуры.

2 посвящен одной знаменитой задаче, играющей важную роль во многих разделах математики и физики, а именно так называемой изопериметрической задаче:

Среди всех плоских фигур данного периметра L найдите ту, которая имеет максимальную площадь.

Как и первые два параграфа 3 содержит ряд теоретических сведений касающихся вписанной, описанной окружности выпуклой фигуры; центра выпуклой фигуры; особое внимание уделено симметризации выпуклой фигуры, а также представлены некоторые задачи на наибольшие и наименьшие значения численных величин, связанных с выпуклыми фигурами. выпуклый фигура изопериметрический экстремум теорема

Основное содержание работы составляет вторая глава, которая состоит из двух параграфов. Данная глава посвящена решению одной красивой задачи, а именно отысканию пятиугольника единичного диаметра, имеющего наибольший периметр. Для решения этой задачи доказывается ряд теорем.

В 1 установив, что диаметр многоугольника совпадает либо с одной из сторон, либо с одной из диагоналей многоугольника (теорема 2.1.1) показывается, что в пятиугольнике наибольшего периметра единичного диаметра, или в оптимальном пятиугольнике, все стороны меньше 1 (теорема 2.1.2). При этом доказательство данной теоремы опирается на лемму о том, что сумма расстояний от точки дуги окружности до ее концов принимает наибольшее значение, когда эта точка делит дугу пополам. Затем в результате последовательного доказательства двух теорем (теорема 2.1.3 и теорема 2.1.4) устанавливается, что в оптимальном пятиугольнике, по крайней мере, четыре диагонали равны 1.

В 2 делается вывод о том, что оптимальным пятиугольником является правильный пятиугольник (теорема 2.2.1).

Было замечено, что в случае выпуклого четырехугольника оптимальным является не квадрат. [2, 269]

Глава 1. Общие сведения о задачах на экстремум. Примеры экстремальных задач