 |
Главная |
Изопериметрическая задача
|
из
5.00
|
Согласно преданию давным-давно финикийская царевна Дидона с небольшим отрядом преданных ей людей покинула родной город Тир, спасаясь от преследований своего брата Пигмалиона. Ее корабли отправились на запад по Средиземному морю, и плыли пока Дидона не заметила удобное для поселения место на африканском побережье, в нынешнем Тунисском заливе. [4, 13]
Король местных жителей нумидийцев Ярб согласился продать Дидоне лишь маленький, по его мнению, участок земли, "в пределах воловьей шкуры". Однако Дидона поступила хитрее. Она разрезала шкуру на тонкие ремни и связала их в одну длинную ленту. Затем перед царевной стояла задача, как этой лентой отгородить участок земли наибольшей площади. Дидона успешно справилась с поставленной задачей и на этом месте основала город Карфаген.
Итак, Дидоне пришлось решать следующую задачу:
Как нужно расположить шнур фиксированной длины L , чтобы он отгораживал от прямолинейного берега участок земли максимальной площади? [4, 14]
Задача Дидоны является частным случаем изопериметрическихзадач. Это название происходит от двух греческих слов: isos - равный и perimetron - обмер, обвод. Изопериметрическая задача состоит в том, чтобы среди данной совокупности фигур, имеющих одинаковую длину контура (одинаковый периметр), найти ту, чья площадь больше площади любой другой фигуры рассматриваемой совокупности.
Рассмотрим простой пример. Пусть выделенный класс геометрических фигур состоит из всех треугольников с данным периметром, тогда изопериметрическая задача заключается в том, чтобы найти треугольник данного периметра, у которого площадь максимальна. Таким треугольником является равносторонний треугольник.
Значительно более сложной является основная изопериметрическая задача:
Среди всех плоских фигур данного периметра L найдите ту, которая имеет максимальную площадь. [5, 22]
Ответом этой задачи является круг. Еще в древней Греции было известно, что круг имеет большую площадь, чем все другие фигуры с тем же самым периметром, а шар — наибольший объем среди всех тел с одной и той же поверхностью. Недаром круг и шар были в древности символами геометрического совершенства. В начале второго века до нашей эры греческий геометр Зенодор написал специальный трактат "О фигурах, имеющих равную периферию". О существовании этого трактата мы узнаем из сочинений греческих комментаторов Зенодора — Паппа (III в. н. э.) и Теона (IV в. н. э.). Сама рукопись Зенодора утеряна. [5, 23]
Хотя ответ в основной изопериметрической задаче и кажется очевидным, строгое ее решение содержит определенные трудности. Швейцарский геометр Штейнер, впервые, доказавший что только круг может служить решением изопериметрической задачи предположил, что фигура наибольшей площади существует. Однако это рассуждение не является строгим. [3, 30]
Рассмотрим общие свойства изопериметрических фигур максимальной площади, для множества фигур на плоскости с данным периметром р.
Свойство 1.2.1. Всякая максимальная фигура выпукла.
Доказательство.
Пусть хорда А1В1, соединяющая точки А1, В1 нашей фигуры, не лежит целиком внутри нее. Тогда, очевидно, некоторый отрезок этой хорды, скажем АВ,лежит весь (кроме концов) вне фигуры. Можно считать поэтому, что дана фигура с периметром АаВС,равным р,не содержащая хорду АВ (рис. 1.2.1). Заменим дугу а хордой АВ.Периметр при такой замене уменьшится, а площадь увеличится на часть АаВ.Построим теперь фигуру, подобную построенной фигуре А 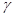 ВС, но с периметром, равным периметру первоначальной фигуры АаВС.У новой фигуры площадь будет больше, чем у второй (поскольку коэффициент подобия больше единицы), и подавно больше, чем у первоначальной.
ВС, но с периметром, равным периметру первоначальной фигуры АаВС.У новой фигуры площадь будет больше, чем у второй (поскольку коэффициент подобия больше единицы), и подавно больше, чем у первоначальной.
Свойство доказано. [5, 24]
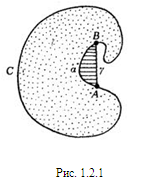
Свойство 1.2.2. Всякая хорда максимальной фигуры с периметром р, делящая пополам ее периметр, обязательно делит ровно пополам и ее площадь.
Доказательство.
Действительно, пусть у фигуры АВС D с периметром р хорда АС делит периметр пополам (рис. 1.2.2). Обозначим через S1, площадь фигуры A ВС,а через S2 - площадь А D С.Предположим, что S1>S2. Построим тогда новую фигуру АВС E А,заменив линию А D С линией АЕС, симметричной с АВС относительно хорды АС.Новая фигура АВСЕА, имея прежний периметр, имеет площадь больше площади первоначальной фигуры, так как площадь новой фигуры равна 2S1, а площадь первоначальной равна S1+S2, в то время как по предположению S1>S2 и, следовательно, 2S1>S1+S2. Поэтому фигура АВС D не является, вопреки предположению, максимальной. Это доказывает, что предположение S1> S2 неверно. Аналогично доказывается, что и предположение S1<S2 приводит к противоречию. Окончательно, S1= S2.
Свойство доказано. [3, 31]
Так как при преобразовании подобия площадь плоской фигуры и квадрат ее периметра увеличиваются или уменьшаются в одинаковое число раз и, следовательно, отношение площади к квадрату периметра не меняется, то задачу можно сформулировать следующим образом:
Среди всех плоских фигур найти фигуру, для которой отношение площади к квадрату периметра было бы наибольшим.[8, 67]
В задаче 1.2.5 доказывается, что если выпуклая фигура Ф отлична от круга, то существует фигура  , имеющая тот же самый периметр, что и Ф, и большую площадь. При этом в задаче 1.2.5 утверждается, что такой фигурой может быть только круг. Таким образом, может показаться, что задача 1.2.5 полностью решает изопериметрическую задачу. Однако, хотя это заключение и является верным (см. задачу 1.2.6), пока мы не имеем оснований делать это заключение с полной определенностью: задача 1.2.5 подсказывает ответ изопериметрической задачи, но не дает ее решения. Яркий пример, показывающий, что существование решения надо доказывать,доставляет следующая модификация парадокса Перрона:
, имеющая тот же самый периметр, что и Ф, и большую площадь. При этом в задаче 1.2.5 утверждается, что такой фигурой может быть только круг. Таким образом, может показаться, что задача 1.2.5 полностью решает изопериметрическую задачу. Однако, хотя это заключение и является верным (см. задачу 1.2.6), пока мы не имеем оснований делать это заключение с полной определенностью: задача 1.2.5 подсказывает ответ изопериметрической задачи, но не дает ее решения. Яркий пример, показывающий, что существование решения надо доказывать,доставляет следующая модификация парадокса Перрона:
Теорема 1.2.1. Среди всех квадратов наибольшую площадь имеет квадрат со стороной 1.
Доказательство
Пусть наибольшую площадь имеет квадрат со стороной a. Рассмотрим два случая: а<1 и a >1. Если а<1, то а2<1 и площадь квадрата со стороной а не является наибольшей (она меньше площади единичного квадрата). Если же а>1, мы возьмем квадрат со стороной b =а2. Тогда b >а (так как а> 1), и площадь квадрата со стороной b будет b 2, притом b 2 >а2 (так как b >а). Значит, квадрат со стороной а не имеет наибольшую площадь, вопреки предположению.
Теорема доказана. [5, 23]
В доказательстве этой теоремы допущена ошибка, а именно не доказано, что существует квадрат наибольшей площади.
Рассмотрим решение задачи Дидоны, пользуясь изопериметрическим свойством круга (см. задачу 1.2.6).
Пусть A ВС и А’В’С’ представляют собой полукруг и какую-нибудь другую фигуру, удовлетворяющую всем условиям задачи. Прибавляя к этим фигурам фигуры А D С и А’ D ’С’, симметричные с первыми относительно осей АС и А’С’,составим две новые фигуры: круг АВС D и отличную от круга фигуру А’В’С’ D ’,периметры которых равны 2 l. Согласно основной теореме об изопериметрах, площадь круга АВС D больше площади фигуры А’В’С’ D ’.Поэтому площадь полукруга АВС больше площади фигуры А’В’С’ и полукруг АВС будет решением задачи Дидоны. [5, 25]
Задачи
Задача №1.2.1.
а) Докажите, что из всех треугольников с двумя заданными сторонами наибольшую площадь имеет тот, у которого эти стороны взаимно перпендикулярны.
б) Докажите, что из двух неравных треугольников, имеющих равные основания и равные углы при противолежащей вершине, большую плошать и больший периметр имеет тот, у которого разность углов при основании меньше (разность боковых сторон меньше); из всех треугольников с данным основанием и данным углом при противолежащей вершине наибольшую площадь и наибольший периметр имеет равнобедренный.
в) Докажите, что из всех параллелограммов с данным острым углом и данным периметром наибольшую площадь имеет ромб.
г) Докажите, что из двух неравных треугольников с одинаковыми основаниями и одинаковыми периметрами большую площадь имеет тот, у которого меньше разность углов при основании (меньше разность боковых сторон); из всех треугольников с данным основанием и данным периметром наибольшую площадь имеет равнобедренный.
д) Докажите, что из всех трапеций с данными основаниями и данным периметром наибольшую площадь имеет равнобокая. [8, 67]
Задача №1.2.2 .
а) Докажите, что из всех треугольников с данным периметром наибольшую площадь имеет равносторонний треугольник.
б) Докажите, что из всех четырехугольников с данным периметром наибольшую площадь имеет квадрат. [7, 335]
Задача №1.2.3.
а) Докажите, что среди всех n-угольников, вписанных в данную окружность, правильный имеет наибольшую площадь.
б) Докажите, что среди всех n-угольников, вписанных в данную окружность, правильный имеет наибольший периметр. [6, 63]
Задача №1.2.4 .
а) Докажите, что из всех выпуклых четырехугольников с данными углами и данным периметром наибольшую площадь имеет четырехугольник, в который можно вписать окружность
б) Докажите, что из всех выпуклых n-угольников с данными углами и данным периметром наибольшую площадь имеет n-угольник, в который можно вписать окружность. [8, 68]
Задача №1.2.5. Докажите, что если выпуклая фигура Ф отлична от круга, то существует фигура  , имеющая тот же самый периметр, что и Ф, и большую площадь. [8, 71]
, имеющая тот же самый периметр, что и Ф, и большую площадь. [8, 71]
Задача №1.2.6. Докажите, что круг имеет большую площадь, чем каждая другая фигура того же периметра. [6, 67]
Решения
Задача №1.2.1
а) Утверждение задачи совершенно очевидно (см. рис. 1.2.3)
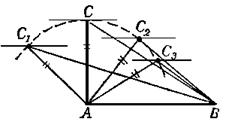
Рис. 1.2.3
б) Наложим два треугольника, удовлетворяющих условию задачи, друг на друга, чтобы их основания совпали, вершины С и С’ были расположены по одну сторону от общего основания АВ и чтобы одновременно выполнялись следующие условия:
 САВ<
САВ<  СВА,
СВА,  С’АВ<
С’АВ<  С’ВА (рис. 1.2.4, а)
С’ВА (рис. 1.2.4, а)
В этом случае вершины С и С’ треугольников будут расположены на дуге окружности ВС’СА,вмещающей угол АСВ,равный углу АС’В (по условию задачи).Из рис. 1.2.4, а)сразу видно, что вершина треугольника АВС,имеющего меньшую разность углов при основании, чем треугольник АВС’,расположена ближе к середине дуги ВС’СА,откуда следует, что высота 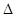 АВС больше высоты
АВС больше высоты 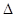 АВС’, и, следовательно, S
АВС’, и, следовательно, S 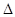 АВС > S
АВС > S 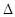 АВС’.
АВС’.
Нам остается еще доказать, что:
СА — СВ < С’А— С’В;
и СА+СВ >С’А+С’В.
Отложим на стороне СА отрезок С D =СВ и на стороне С’А отрезок С’ D ’= С’В и соединим D и D ’ с В (рис. 1.2.4,а).Так как углы А D В и А D ’ B этовнешние углы равнобедренных треугольников BCD и BC ’ D ’ то:
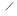 ADB =2 d -
ADB =2 d - 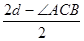 =
= 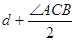 ,где d =90°.
,где d =90°.
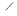 AD ’ B = d +
AD ’ B = d +  .
.
Так как 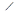 ADB =
ADB = 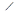 А D ’В,то точки D и D ’ лежат на дуге окружности BD ’ DA.Поскольку
А D ’В,то точки D и D ’ лежат на дуге окружности BD ’ DA.Поскольку 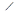 D ВА <
D ВА < 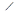 D ’ВА < 180°, то CA - CB = DA < D ’ A = C ’ A - C ’ B.
D ’ВА < 180°, то CA - CB = DA < D ’ A = C ’ A - C ’ B.
Аналогично, отложив на продолжении сторон BC и BC ’ отрезки CE = CA и C ’ E ’= C ’ A (рис. 1.2.4, б) получим:
СА+СВ = ВЕ> ВЕ’ = С’А+ С’В,
так как 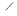 АЕВ=
АЕВ= 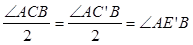 .
.
Второе утверждение задачи сразу следует из доказанного.
в) Параллелограмм с данным острым углом а и данным периметром 2р разбивается диагональю на два треугольника. Поэтому для решения задачи нам достаточно доказать, что из всех треугольников с данным углом а при вершине и данной суммой р боковых сторон наибольшую площадь имеет равнобедренный треугольник.
Итак, пусть АВС — такой разносторонний треугольник, что:
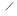 ВАС = а,а АВ+АС = р;
ВАС = а,а АВ+АС = р;
предположим для определенности, что АВ>АС (в противном случае доказательство аналогично). Построим равнобедренный треугольник АВ’С’,у которого 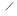 В’АС’ = а, АВ’+АС’ = р и который расположен, как указано на рис. 1.2.5. Точку пересечения сторон ВС и В’С’ обозначим через М.Докажем теперь, что:
В’АС’ = а, АВ’+АС’ = р и который расположен, как указано на рис. 1.2.5. Точку пересечения сторон ВС и В’С’ обозначим через М.Докажем теперь, что:
S  CC’M>S
CC’M>S  BB’M
BB’M
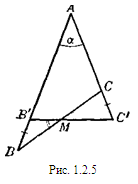
Действительно, треугольники СС’М и ВВ’М имеют равные углы при вершинах и равные основания СС’ и ВВ’:
СС’ — ВВ’ = (АС’ — АС) — (АВ — АВ’)= (АВ’ +АС’)— (АВ + АС) =р — р = 0.
Далее, из четырех углов ВВ’М, В’ВМ, СС’М и С’СМ наибольшим является первый, а следовательно, наименьшим — второй (т.к. сумма двух первых углов равна сумме двух последних). Отсюда следует, что разность углов при основании треугольника ВВ’М больше, чем разность углов при основании треугольника СС’М.Таким образом S  CC’M>S
CC’M>S  BB’M. Следовательно, S
BB’M. Следовательно, S  AB’C’>S
AB’C’>S  ABC , что и требовалось доказать. [8, 221]
ABC , что и требовалось доказать. [8, 221]
г) Наложим два треугольника, удовлетворяющих условию задачи, друг на друга так, чтобы их основания совпали, вершины С и С’ были расположены по одну сторону от общего основания АВ,пусть при этом:
 САВ<
САВ< 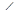 СВА;
СВА;
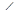 С’АВ<
С’АВ< 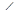 С’ВА,
С’ВА,
пустькроме этого
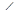 САВ>
САВ> 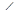 С’ AB (рис.1.2.6).
С’ AB (рис.1.2.6).
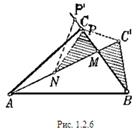
Если бы при этом был 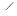 СВА>
СВА> 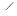 С’ВА,то
С’ВА,то 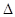 C ’ BA был бы заключен внутри треугольника
C ’ BA был бы заключен внутри треугольника 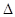 ABC и они не могли бы иметь равных периметров. Следовательно, треугольники расположены так, как изображено на рис. 1.2.6; отсюда и из предыдущих соотношений между углами следует, что разность углов при основании больше у треугольника АС’В (
ABC и они не могли бы иметь равных периметров. Следовательно, треугольники расположены так, как изображено на рис. 1.2.6; отсюда и из предыдущих соотношений между углами следует, что разность углов при основании больше у треугольника АС’В ( 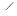 CBA -
CBA - 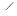 CAB <
CAB < 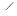 CBA-
CBA- 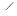 C ’ AB<
C ’ AB< 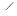 C ’ BA-
C ’ BA- 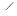 C ’ AB). Точку пересечения сторон АС’ и ВС обозначим через М.Отложим на прямой МА отрезок MN = MB и на прямой МС отрезок МР=МС’. При этом точка N будет находиться между А и М,так как из того, что:
C ’ AB). Точку пересечения сторон АС’ и ВС обозначим через М.Отложим на прямой МА отрезок MN = MB и на прямой МС отрезок МР=МС’. При этом точка N будет находиться между А и М,так как из того, что:
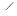 МВА >
МВА > 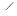 САВ >
САВ > 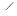 МАВ, следует, что МА > МВ.
МАВ, следует, что МА > МВ.
С другой стороны, точка Р будет находиться между М и С,так как если бы она совпала с некоторой точкой Р’ на продолжении МС,то из равенства периметров двух треугольников мы имели бы
АС+СВ=АС’+С’В, т.е. АС+Р’М-СР’+МВ = А N + N М+ MC ’+С’В.
Отсюда, так как:
Р’М=МС’, МВ=М N и С’В=Р’ N,
мы имели бы:
АС=АN + N Р’+Р’С,
что невозможно.
Отняв теперь от треугольников АВС и АВС’ равные между собой треугольники N МР и МВС’ (заштрихованные на рис. 1.2.6), мы сразу обнаружим, что треугольник АВС имеет большую площадь.
Нам еще остается доказать, что:
СА — СВ< С’А — С’В.
Для этого достаточно проверить, что АС<АС’ (а следовательно, ВС>ВС’). Действительно, если бы было АС>АС’, ВС<ВС’, то из рассмотрения треугольников АСС’ и ВСС’ мы получили бы два несовместных неравенства:
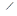 АСС’<
АСС’< 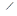 АС’С,
АС’С, 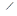 ВСС’>
ВСС’> 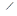 ВС’С.
ВС’С.
Равенство же АС=АС’ невозможно, так как треугольники АВС и АВС’,по предположению, не равны.
Второе утверждение задачи сразу следует из доказанного. [8, 223]
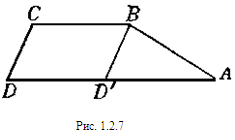
д) Для того чтобы при заданных условиях площадь трапеции АВС D была наибольшей, необходимо, чтобы ее высота была наибольшей. Проведя линию В D ’ || С D (рис. 1.2.7), мы получим, что наибольшей высоте трапеции АВС D отвечает наибольшая площадь треугольника АВ D ’ с заданным основанием (равным разности оснований трапеции) и заданным периметром (равным периметру трапеции минус удвоенное меньшее основание). После этого остается только применить к треугольнику АВ D ’ заключение задачи 1.2.1 пункта г. [8, 224]
Задача №1.2.2
а) Эта несложная задача имеет несколько решений, мы рассмотрим только два.
Первое решение.
По формуле Герона площадь S треугольника со сторонами a , b , с и полупериметром р равна:
S= 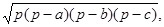
откуда:
S2=p( p-a)( p-b)( p-c).
Но так как:
(p - a)+(p - b)+(p - c)=3 p -(a + b + c)=3 p -2 p = p,
то по теореме о среднем арифметическом и среднем геометрическом:
(p - a)(p - b)(p - c) 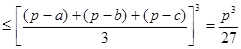
и, следовательно, S2 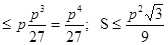 , где равенство имеет место лишь в случае p - a = p - b = p - c , т.е. в случае a = b = c, - когда
, где равенство имеет место лишь в случае p - a = p - b = p - c , т.е. в случае a = b = c, - когда  ABC является равносторонним. [6, 253]
ABC является равносторонним. [6, 253]
Второе решение
Пусть АВС—неравносторонний треугольник, АВ— его большая сторона (или одна из двух больших сторон) (рис. 1.2.8, а).
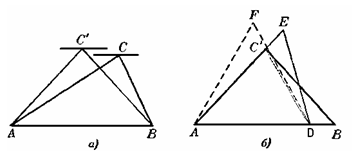
Рис. 1.2.8
Равнобедренный треугольник АВС’,имеющий тот же периметр, что и треугольник АВС,и то же основание АВ (рис. 1.2.8, а), в силу задачи 1.2.1 г) имеет не меньшую площадь, чем треугольник АВС.Построим теперь треугольник А D Е, у которого сторона А D равна  периметра треугольника АВС’ (или АВС),
периметра треугольника АВС’ (или АВС),  D АЕ=
D АЕ=  ВАС’ и периметр которого равен периметру
ВАС’ и периметр которого равен периметру  АВС’.Расположим треугольник А D Е так, как указано на рис. 1.2.8, б).Так как АВ — большая сторона треугольника АВС,а сторона А D равна трети периметра этого треугольника, то АВ>А D;отсюда следует, что АЕ>АС’ (так как иначе
АВС’.Расположим треугольник А D Е так, как указано на рис. 1.2.8, б).Так как АВ — большая сторона треугольника АВС,а сторона А D равна трети периметра этого треугольника, то АВ>А D;отсюда следует, что АЕ>АС’ (так как иначе  А D Е был бы заключен внутри треугольника АВС’ и не мог бы иметь того же периметра). Так как АВ это большая сторона равнобедренного треугольника АВС’,поэтому:
А D Е был бы заключен внутри треугольника АВС’ и не мог бы иметь того же периметра). Так как АВ это большая сторона равнобедренного треугольника АВС’,поэтому:
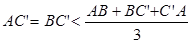 =AD.
=AD.
Из последнего неравенства вытекает, что  АС’ D >
АС’ D > 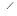 А D С’,т. е.
А D С’,т. е. 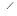 ЕС’ D <
ЕС’ D < 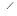 В D С’.
В D С’.
Так как, кроме того, очевидно, что 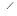 В D С’>
В D С’> 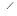 Е D С’,то в силу задачи 1.2.1 г) мы можем заключить, что из двух треугольников С’ D Е и ВС’ D,имеющих общее основание и равные периметры (т.к. периметр треугольника АВС’ равен периметру треугольника А D Е,то AC ’+ C ’ E + ED + DA = AC ’+ C ’ B + BD + DA,значит C ’ E + ED = C ’ B + BD), второй имеет меньшую площадь. Таким образом,
Е D С’,то в силу задачи 1.2.1 г) мы можем заключить, что из двух треугольников С’ D Е и ВС’ D,имеющих общее основание и равные периметры (т.к. периметр треугольника АВС’ равен периметру треугольника А D Е,то AC ’+ C ’ E + ED + DA = AC ’+ C ’ B + BD + DA,значит C ’ E + ED = C ’ B + BD), второй имеет меньшую площадь. Таким образом,
S 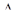 C’ DE>S
C’ DE>S 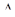 BC’ D, S
BC’ D, S 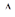 A DE>S
A DE>S  ABC’.
ABC’.
Теперь, построив на основании А D равнобедренный треугольник А DF , имеющий тот же периметр, что и треугольник А D Е (этот треугольник, изображенный пунктиром на рис. 1.2.8, б),очевидно, будет равносторонним (т.к. AD= 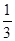 p, AF=FD=
p, AF=FD= 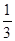 p), мы получим согласно задаче 1.2.1 г), что:
p), мы получим согласно задаче 1.2.1 г), что:
S  ADF > S
ADF > S  ADE
ADE
(треугольник А D Е не совпадает с равносторонним треугольником А DF,так как 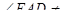 60°).
60°).
Цепь неравенств:
S  ABC
ABC  S
S 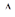 ABC’< S
ABC’< S 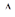 ADE < S
ADE < S 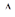 ADF
ADF
и доказывает теорему (в этом ряду неравенств мы один раз вынуждены писать 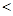 вместо <, так как у нас нет уверенности, что
вместо <, так как у нас нет уверенности, что  АВС не равен
АВС не равен  A ВС’,т. е. что он не равнобедренный). [8, 225]
A ВС’,т. е. что он не равнобедренный). [8, 225]
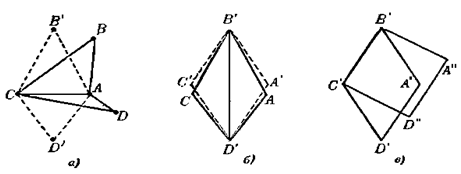
Рис. 1.2.9
б) Разобьем четырехугольник АВС D диагональю АС на два треугольника. Заменив треугольники A ВС и АС D равнобедренными треугольниками АВ’С и АС D ’ с теми же основаниями и с теми же периметрами, мы получим четырехугольник АВ’ CD ’, причем в силу задачи 1.2.1 г):
SAB’CD’  SABCD (рис. 1.2. 9, а).
SABCD (рис. 1.2. 9, а).
Теперь заменим равные треугольники АВ’ D ’ и В’С D ’ (по трем сторонам)равнобедренными треугольниками А’В’ D ’ и В’С’ D ’ с теми же основаниями и теми же периметрами; мы получим ромб А’В’С’ D ’,причем:
SA’B’C’D ’  SAB’CD’ (рис. 1.2.9, б).
SAB’CD’ (рис. 1.2.9, б).
Наконец, ромб А’В’С’ D ’ имеет в силу задачи 1.2.1 а) не большую площадь, чем квадрат А’’ B ’С’ D ’’ с той же стороной (рис. 1.2.9, в).
Если четырехугольник АВС D отличен от квадрата, то в цепи неравенств:
SABCD 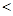 SAB’CD’
SAB’CD’ 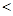 SA’B’C’D’
SA’B’C’D’ 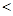 SA’’B’C’D’’,
SA’’B’C’D’’,
хотя бы один раз должно стоять точное неравенство. [8, 227]
Задача №1.2.3
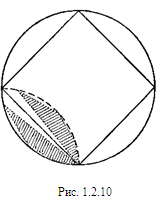
а) Если вписанный в круг n-угольник не является правильным, то у него есть сторона, меньшая стороны соответствующего правильного n-угольника. Предположим, что у этого вписанного в круг неправильного n-угольника есть сторона, большая стороны правильного n-угольника (если это не так, то весь n-угольник вписан в дугу окружности, меньшую 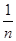 — части окружности; этот случай можно отбросить, так как тогда многоугольник может быть целиком помещен внутри правильного n-угольника и иметь в этом случае меньшую площадь; рис. 1.2.10).
— части окружности; этот случай можно отбросить, так как тогда многоугольник может быть целиком помещен внутри правильного n-угольника и иметь в этом случае меньшую площадь; рис. 1.2.10).
Не меняя площади многоугольника, вписанного в окружность, мы можем поменять его стороны местами так, чтобы рядом оказались сторона, большая стороны правильного n-угольника, и сторона, меньшая стороны правильного n-угольника (очевидно, что если поменять местами две соседние стороны вписанного в окружность многоугольника, то площадь его не изменится (рис. 1.2.11); повторяя этот процесс, можно добиться того, чтобы любые две стороны оказались рядом).
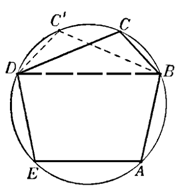
Рис. 1.2.11
Если мы теперь, не меняя остальных сторон, изменим длины этих двух сторон многоугольника так, чтобы одна из них стала равной стороне правильного n-угольника и многоугольник оставался вписанным в ту же окружность, то согласно задаче 1.2.1, 6) площадь n-угольника увеличится. Продолжая этот процесс далее, мы придем, в конце концов, к правильному n-угольнику; при этом в процессе изменения исходного n-угольника площадь его будет только увеличиваться.
б) Доказывается аналогично решению задачи 1.2.3 а). [6, 251]
Задача №1.2.4
а) Примем известный периметр искомого четырехугольника ABCD за единицу и пусть A ’ B ’ C ’ D ’, какой лидо четырехугольник подобный ABCD. Тогда площадь ABCD равна отношению 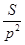 площади четырехугольника A ’ B ’ C ’ D ’ к квадрату его периметра (т.к. коэффициент подобия четырехугольников ABCD и A ’ B ’ C ’ D ’ равен отношению их периметров т.е.
площади четырехугольника A ’ B ’ C ’ D ’ к квадрату его периметра (т.к. коэффициент подобия четырехугольников ABCD и A ’ B ’ C ’ D ’ равен отношению их периметров т.е. 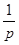 , а площадь ABCD равна площади A ’ B ’ C ’ D ’ умноженной на квадрат коэффициента подобия, т.е. равна S
, а площадь ABCD равна площади A ’ B ’ C ’ D ’ умноженной на квадрат коэффициента подобия, т.е. равна S 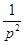 =
= 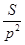 ) и задача сводится к тому, что бы найти тот из четырехугольников, имеющий наперед заданные углы, для которого отношение площади к квадрату периметра имеет наибольшее возможное значение (рис. 1.2.12). Нам требуется доказать, что искомым будет четырехугольник ABCD который можно описать около окружности. [6, 247]
) и задача сводится к тому, что бы найти тот из четырехугольников, имеющий наперед заданные углы, для которого отношение площади к квадрату периметра имеет наибольшее возможное значение (рис. 1.2.12). Нам требуется доказать, что искомым будет четырехугольник ABCD который можно описать около окружности. [6, 247]
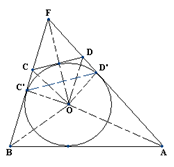
Рис. 1.2.12
Постоим треугольник АВ F два угла которого равны углам А и В искомого четырехугольника (такой треугольник невозможно построить лишь в том случае, когда сумма каждых двух соседних углов четырехугольника ABCD равна 1800. В этом исключительном случае наша задача формулируется так: доказать, что из всех параллелограммов с данным острым углом и данным периметром наибольшую площадь имеет ромб). Нам надо пересечь этот треугольник прямой CD данного направления, так, чтобы у получившегося четырехугольника ABCD отношение площади к квадрату периметра было возможно большим. Впишем в треугольник ABF окружность с радиусом r и центром О и проведем прямую CD заданного направления таким образом, что бы она касалась этой окружности (рис. 1.2.12). Докажем, что четырехугольник ABCD обладает требуемым свойством, т.е., если C ’ D ’ – произвольная прямая параллельная CD, то:
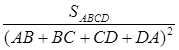
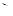
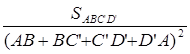 (*)
(*)
Обозначим коэффициент подобия треугольников FCD и FC ’ D ’ через k (k может быть больше или меньше единицы). Очевидно, что:
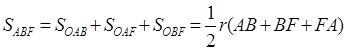 ;
;
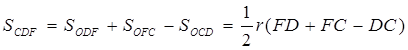 ;
;
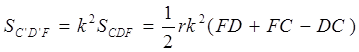 . [6, 248]
. [6, 248]
Отсюда:
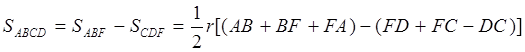 ;
;
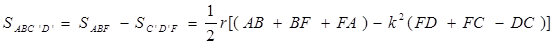
или, если обозначить
AB + BF + FA через 2p, а CF + FD - DC- через 2q:
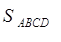 = r (p-q);
= r (p-q);
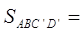 r (p-k 2q).
r (p-k 2q).
Далее, из подобия треугольников CDF и C ’ D ’ F следует:
C ’ F + FD ’- C ’ D ’=2kq, откуда AB + BC + CD + DA = AB + BF + FA -(CF + FD - CD)=2(p-q),
AB + BC ’+ C ’ D ’+ D ’ A = AB + BF + FA -(C ’ F + FD ’- C ’ D ’)=2(p-kq).
В силу этого неравенство (*) примет следующий вид:
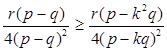 , откуда имеем:
, откуда имеем:
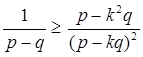 .
.
Перенося оба члена неравенства в левую часть и умножая его на (положительное) число (p-q) (p-k q) 2, получим:
(p-k q) 2 - (p-q) (p-k 2q)  0,
0,
что после раскрытия скобок и упрощения дает:
(1- k) 2 p q  0.
0.
Последнее неравенство очевидно справедливо. [6, 249]
б) Для простоты решим сначала задачу для случая пятиугольника, и пусть М=АВС D Е иM’= А’В’С’ D ’Е’- два пятиугольника с периметрами Р и Р’ и площадями S и S’, имеющие равные углы, причем М описан вокруг окружности s радиуса r, а M’ не подобен М. Для того что бы доказать неравенство:
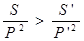 (**)
(**)
отбросим соответствующие стороны D Е и D ’ E ’ пятиугольников М и М’ (такие, что  D +
D +  Е=
Е=  D ’+
D ’+  E ’>1800) и продолжим примыкающие к D Е и D ’ E ’ стороны до их пересечения. При этом мы получим два четырехугольника ABCT и A ’ B ’ C ’ T ’ с соответственно равными углами, причем четырехугольник ABCT описан вокруг окружности s (рис. 1.2.13). Для упрощения выкладок будем считать, что размеры исходных пятиугольников выбраны так, что рассматриваемые четырехугольники имеют одинаковые периметры, равные Р1 (выполнение этого условия всегда можно добиться, преобразовав, если надо, пятиугольник М’ подобно).
E ’>1800) и продолжим примыкающие к D Е и D ’ E ’ стороны до их пересечения. При этом мы получим два четырехугольника ABCT и A ’ B ’ C ’ T ’ с соответственно равными углами, причем четырехугольник ABCT описан вокруг окружности s (рис. 1.2.13). Для упрощения выкладок будем считать, что размеры исходных пятиугольников выбраны так, что рассматриваемые четырехугольники имеют одинаковые периметры, равные Р1 (выполнение этого условия всегда можно добиться, преобразовав, если надо, пятиугольник М’ подобно).
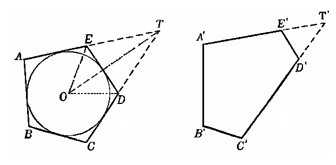
Рис. 1.2.13
Ясно, что 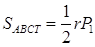 . Обозначим
. Обозначим 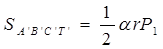 , где
, где 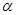 - некоторое положительное число (равное
- некоторое положительное число (равное 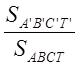 ). [6, 250]
). [6, 250]
В силу результата задачи а) 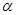
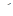 1, причем
1, причем 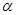 =1, лишь, если A ’ B ’ C ’ T ’ тоже описан около окружности, т.е. если он равен ABCT.
=1, лишь, если A ’ B ’ C ’ T ’ тоже описан около окружности, т.е. если он равен ABCT.
Далее обозначим DT +ТЕ- D Е= p и D ’ T ’+Т’Е’- D ’Е’= kp , где k - коэффициент подобия треугольников 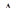 D ’ E ’ T ’ и
D ’ E ’ T ’ и  DTE.Так как
DTE.Так как
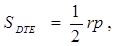 то
то 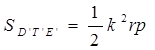 .
.
Далее имеем:
S=S M = 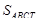 -
- 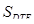 ;
;
P=AB+BC+CD+DE+EA=(AB+BC+CT+TA)- (DT+TE-ED).
S’=S M’ = 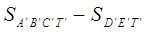
P’ = A’B’+B’C’+C’D’+D’E’+E’A’=(A’B’+B’C’+C’T’+T’A’)- (D’T’+T’E’-E’D’).
Поэтому неравенство (**) примет вид:
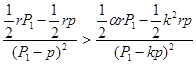 или
или 
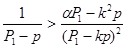 ,
,
т.е. 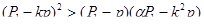 .
.
Но последнее неравенство действительно справедливо:
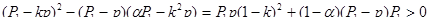 ,
,
так как 1- 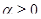 ,а
,а 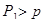 по самому определению этих величин. В последнем неравенстве стоит знак >, а не
по самому определению этих величин. В последнем неравенстве стоит знак >, а не 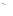 так как если 1-
так как если 1- 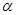 =0,
=0, 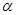 =1, то четырехугольник А’В’С’Т’ равен четырехугольнику АВСТ, и для того, чтобы пятиугольник А’В’С’ D ’Е’ был отличен от АВС D Е,надо, чтобы треугольник D ’Е’Т’ был отличен от D ЕТ,т. е. что бы было k
=1, то четырехугольник А’В’С’Т’ равен четырехугольнику АВСТ, и для того, чтобы пятиугольник А’В’С’ D ’Е’ был отличен от АВС D Е,надо, чтобы треугольник D ’Е’Т’ был отличен от D ЕТ,т. е. что бы было k  1; таким образом, если (1—а)(Р1 — p)Р1 =0, то Р1 р(1—к)2 больше нуля.
1; таким образом, если (1—а)(Р1 — p)Р1 =0, то Р1 р(1—к)2 больше нуля.
Решение задачи для n-угольника проводится по методу математической индукции. Оно ничем не отличается от выше приведенного, и все выкладки имеют точно такой же вид. Только вместо пятиугольника всюду надо говорить об n-угольнике и вместо четырехугольника - об (п-1)-угольнике, для которого, по предположению индукции, теорема считается уже доказанной (что позволяет утверждать, что 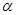
 1). [6, 251]
1). [6, 251]
Задача №1.2.5
Пусть АВ — хорда фигуры Ф, делящая периметр Ф пополам. Если хорда АВ делит площадь Ф на две неравные части, то существует фигура  , имеющая тот же периметр, что и Ф, и большу
, имеющая тот же периметр, что и Ф, и большу
|
из
5.00
|
Обсуждение в статье: Изопериметрическая задача |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

