 |
Главная |
Напряжённое состояние в точке
|
из
5.00
|
Вспомним, как нами было введено понятие напряжения. Рассмотрим тело, находящееся под действием системы уравновешенных сил (рис.48).
 |


Рис.48
Будем исследовать внутренние силы в малой области окружающей точку  , для чего проведём через данную точку сечение, рассекая тело на две части, и отбросим одну из них. Действие отброшенной части заменим внутренними силами (рис.49).
, для чего проведём через данную точку сечение, рассекая тело на две части, и отбросим одну из них. Действие отброшенной части заменим внутренними силами (рис.49).

Рис. 49
Выделим малую площадку  , содержащую точку
, содержащую точку  . Внешнюю нормаль этой площадки обозначим
. Внешнюю нормаль этой площадки обозначим 
 .
.
Результирующую внутренних сил, действующих на площадку  , обозначим
, обозначим  . Деля результирующую
. Деля результирующую  на
на  получим величину среднего напряжения по площадке
получим величину среднего напряжения по площадке

Величина  зависит от размеров площадки. Чтобы избавиться от влияния размеров площадки
зависит от размеров площадки. Чтобы избавиться от влияния размеров площадки  , перейдём к пределу и будем стягивать площадку к точке
, перейдём к пределу и будем стягивать площадку к точке 
 (1)
(1)
Величину  будем называть полным напряжением в точке
будем называть полным напряжением в точке  по площадке с внешней нормалью
по площадке с внешней нормалью  .
.
Совершенно очевидно, что если мы выберем другую площадку, проходящую через точку  , но ориентированную другим образом, то в общем случае вектор полного напряжения окажется иным.
, но ориентированную другим образом, то в общем случае вектор полного напряжения окажется иным.
Совокупность всех векторов полного напряжения по всем площадкам, проходящим через данную точку, составляет напряженное состояние в данной точке.
Напряжённое состояние в данной точке известно, если известны напряжения по трём взаимно перпендикулярным площадкам, проходящим через данную точку.
Докажем это важнейшее положение.
Нас интересует напряжённое состояние в точке  . Выделим в окрестности этой точки малый прямоугольный параллелепипед (рис.50). Размеры параллелепипеда настолько малы, что напряжённое состояние в пределах параллелепипеда можно считать однородным, и что грани параллелепипеда являются площадками, проходящими через точку
. Выделим в окрестности этой точки малый прямоугольный параллелепипед (рис.50). Размеры параллелепипеда настолько малы, что напряжённое состояние в пределах параллелепипеда можно считать однородным, и что грани параллелепипеда являются площадками, проходящими через точку  и имеющими внешними нормалями оси
и имеющими внешними нормалями оси 

Рис. 50
Полное напряжение можно разложить на три составляющие, направленные по координатным осям. Всего будем иметь 9 компонент напряжённого состояния: три нормальных и шесть касательных напряжений. Нормальные напряжения обозначим  и припишем индекс, указывающий внешнюю нормаль.
и припишем индекс, указывающий внешнюю нормаль.
Например: 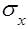 — нормальное напряжение по площадке с внешней нормалью
— нормальное напряжение по площадке с внешней нормалью  .
.
Касательные напряжения обозначаются  с двумя индексами. Первый индекс указывает площадку, второй – направление напряжения.
с двумя индексами. Первый индекс указывает площадку, второй – направление напряжения.
Например  — касательное напряжение по площадке с внешней нормалью
— касательное напряжение по площадке с внешней нормалью  , параллельное оси Y .
, параллельное оси Y .
Нормальное напряжение считается положительным, если оно направлено по внешней нормали, т.е. является растягивающим.
Касательные напряжения считаются положительными, если при положительной внешней нормали они направлены в сторону положительных координатных осей.
Совершенно очевидно, что по противоположным граням параллелепипеда действуют равные по величине и противоположные по направлению напряжения.
Заметим также, что хотя на рис.50 компоненты напряжённого состояния показаны в виде векторов, они являются величинами скалярными.
Докажем, что касательные напряжения по взаимно перпендикулярным площадкам равны. Т.к. тело, из которого вырезан элементарный параллелепипед, находится в равновесии, то условия равновесия применимы и к элементу объёма. Запишем условие, что сумма моментов всех сил приложенных к элементарному параллелепипеду относительно координатных осей равна нулю



Раскроем первое из этих уравнений
 ,
,
откуда 
т.е. закон парности касательных напряжений.
Два других уравнения дадут равенства:
 ;
; 
Таким образом, независимых составляющих 6.
А теперь докажем положение высказанное на стр.2 о том, что зная напряжения, действующие по любым трём взаимно перпендикулярным площадкам, можно определить напряжения по любой площадке, проходящей через данную точку.
Вырежем в окрестности исследуемой точки элементарный тетраэдр с бесконечно малыми рёбрами. Три грани тетраэдра параллельны координатным плоскостям, а четвёртая наклонна к первым трём и её внешняя нормаль 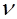 (рис.51).
(рис.51).
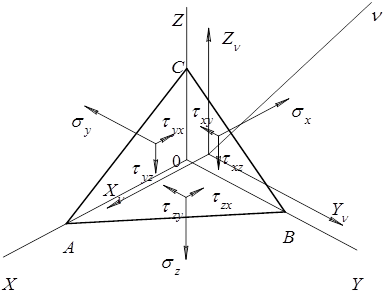 |
Рис. 51
Напряжения
 (2)
(2)
возникающие по площадкам с внешними нормалями  считаем известными.
считаем известными.
Нужно найти полное напряжение по площадке с внешней нормалью  —
—  . Составляющие полного напряжения, направленные по координатным осям обозначим
. Составляющие полного напряжения, направленные по координатным осям обозначим  .
.
Направляющие косинусы нормали обозначим:
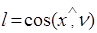 ;
;  ;
;  (3)
(3)
Если принять площадь грани  —
—  , то площади остальных граней
, то площади остальных граней
 ;
;  ;
; 
Составим уравнения равновесия для тетраэдра



Используя также условия  ;
;  , получаем следующие соотношения
, получаем следующие соотношения

 (4)
(4)

Совокупность 6 компонент напряжённого состояния (2) составляет тензор напряжений. Зная тензор напряжений (2), можно с помощью соотношений (4) определить напряжения по любой площадке в данной точке.
Величина полного напряжения определится

Для того чтобы определить нормальное напряжение по площадке с внешней нормалью 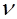 , надо спроектировать на нормаль составляющие полного напряжения
, надо спроектировать на нормаль составляющие полного напряжения  (рис.52).
(рис.52).
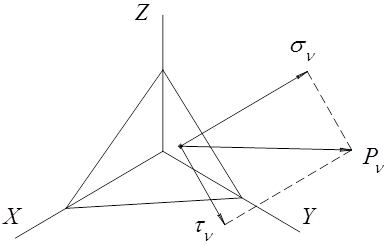 |
Рис. 52
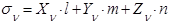
Подставляя выражение (4), получаем:
 (5)
(5)
Касательное напряжение определяется

Главные напряжения
В окрестности любой точки существуют три взаимно перпендикулярные площадки, касательные напряжения по которым равны нулю. Эти площадки называются главными, а напряжения, действующие на них главными напряжениями.
Покажем, как находить главные напряжения и главные площадки в общем случае.
Допустим, что главная площадка существует и её внешняя нормаль 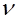 . Главное напряжение совпадает по направлению с внешней нормалью
. Главное напряжение совпадает по направлению с внешней нормалью 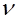 и составляющие напряжения
и составляющие напряжения  по координатным осям равны:
по координатным осям равны:
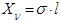
 (6)
(6)

Внесём выражения (6) в уравнения (4) и получим систему трёх уравнений однородных относительно направляющих косинусов  ,
, 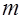 ,
, 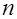 :
:
 (7)
(7)
Кроме того, направляющие косинусы связаны между собой соотношением
 (8)
(8)
В силу соотношения (7) система (6) не может иметь тривиального решения:  ,
, 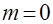 ,
,  , следовательно, определитель системы (6) должен быть равен нулю.
, следовательно, определитель системы (6) должен быть равен нулю.

Раскроем определитель


Или

Полученное кубическое уравнение перепишем:
 , (9)
, (9)
где коэффициенты имеют следующее выражение


т.е.  равняется сумме миноров элементов, стоящих на главной диагонали определителя, составленного из компонентов тензора напряжений (2)
равняется сумме миноров элементов, стоящих на главной диагонали определителя, составленного из компонентов тензора напряжений (2)

т.е.  равняется определителю, составленному из компонентов тензора напряжений (2). Т.к. матрица, составленная из компонентов тензора напряжений симметрична, уравнение (9) имеет три действительных корня — три главных напряжения, которые пронумеруем в порядке их алгебраической величины
равняется определителю, составленному из компонентов тензора напряжений (2). Т.к. матрица, составленная из компонентов тензора напряжений симметрична, уравнение (9) имеет три действительных корня — три главных напряжения, которые пронумеруем в порядке их алгебраической величины

Главные напряжения в данной точке при заданном напряжённом состоянии не могут зависеть от выбора исходных площадок, т.е. от выбора координатных осей, следовательно, коэффициенты уравнения (8) инварианты по отношению к выбору системы координат. Они называются инвариантами тензора напряжений
 — линейный инвариант
— линейный инвариант
 — квадратичный инвариант
— квадратичный инвариант
 — кубичный инвариант
— кубичный инвариант
Найдя из уравнения (9) главные напряжения и внося их в любые 2 уравнения (7) и добавляя соотношение (8) находим направляющие косинусы главных площадок.
|
из
5.00
|
Обсуждение в статье: Напряжённое состояние в точке |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

