Дисперсия частот атомных колебаний

СОДЕРЖАНИЕ

 

СОДЕРЖАНИЕ

ГЛАВА 1. КОЛЕБАНИЯ АТОМОВ В ОДНОМЕРНОЙ ЦЕПИ

§1.1 Уравнение движения

§ 2.1 Статистика Бозе--Энштейна

ЗАКЛЮЧЕНИЕ

ЛИТЕРАТУРА

 

ВВЕДЕНИЕ

 

Исследуя структуру вещества, ученые научились разглядывать отдельные атомы – пространственное разрешение сканирующих туннельных микроскопов вполне для этого достаточно. Однако временное разрешение до сих пор оставалось не важным.

Все, что видели экспериментаторы, это усредненное по времени положение атомов; отслеживать отдельные движения на атомном масштабе пока не удавалось. И вот, в недавних экспериментах группа американских ученных преодолела этот рубеж. Они смогли наблюдать колебания пока не атомов твердого тела, но уже их небольших групп. Они смогли увидеть фононы: как они осциллируют во времени. Из этого следует, что фононы привлекали интерес многих ученых мира, и будут привлекать до тех пор, пока они не будут изучены досконально. Именно этим и обусловлен выбор данной темы курсовой работы.

Именно фононы являются, как говорят физики, истинными степенями свободы в кристаллическом твердом теле. В терминах фононов можно описать и звуковые волны, и теплоемкость кристалла, и сверхпроводимость некоторых материалов, и, наконец, самые разнообразные микроскопические явления в кристалле.

В связи с выше сказанным целью данной курсовой работы является:

1. Изучение основ теории динамики кристаллической решетки, а именно колебаний атомов в одномерной цепи и непосредственно фононов.

2. Изучение статистики, которой подчиняются фононы, – статистики Бозе - Эйнштейна.

3.Рассмотрение фононного спектра и плотности фононных состояний.

Концепция фонона оказалась очень плодотворной в физике твёрдого тела. В кристаллических материалах атомы активно взаимодействуют между собой, и рассматривать в них такие термодинамические явления, как колебания отдельных атомов, затруднительно — получаются огромные системы из триллионов связанных между собой линейных дифференциальных уравнений, аналитическое решение которых невозможно. Колебания атомов кристалла заменяются распространением в веществе системы звуковых волн, квантами которых и являются фононы.

ГЛАВА 1. КОЛЕБАНИЯ АТОМОВ В ОДНОМЕРНОЙ ЦЕПИ

Уравнение движения

 

Кристалл представляет собой совокупность атомов, связанных упругими силами. Атомы взаимодействуют между собой с помощью различных сложных сил. Имеются как слабые, так и сильные взаимодействия, а также существуют силы притяжения и отталкивания, которые действуют на атомы и в точках устойчивого равновесия взаимно уравновешивают друг друга[5].

Каждый из атомов непрерывно движется (в частности колеблется) в области пространства с центром в узле кристаллической решетки. При этом они локализованы в объеме, который имеет определенную величину для каждого атома; объемы занятые различными атомами не перекрываются.

Узлы решетки – это положения равновесия для атомов, т.е. это точки, в которых уравновешиваются силы притяжения и отталкивания. При смещении атома силы перестают быть скомпенсированными и действуют так, чтобы уменьшить это смещение.

Атом имеет потенциальную энергию взаимодействия с каждым другим атомом в твердом теле, но за пределами некоторого расстояния, энергия взаимодействия становится пренебрежимо малой.

Вследствие этого в энергию взаимодействия необходимо включать только те атомы, которые находятся на разумном расстоянии от этого рассматриваемого атома. Число соседей, которое следует включить, определяется тем, как сила взаимодействия совпадает с расстоянием.

Атомы кристалла покоятся в узлах решетки только при абсолютном нуле температуры. При повышении температуры атомы начинают колебаться около своих положений устойчивого равновесия, поэтому нам необходимо рассмотреть динамику движения атомов в кристалле.

Рассмотрим простейший случай колебания одинаковых атомов в одномерной (линейной) решетке, подчиняющихся в своем движении законам классической механики.

 

Рисунок 1.Однородная линейная цепочка атомов

m₀ – масса атома.

а – расстояние между атомами.

 

Закономерности, полученные для такой схематической одномерной модели, оправдываются и для трехмерных решеток. Кроме того, при достаточно высоких температурах движение атомов в кристалле действительно подчиняется законам классической механики.

Допустим, что вдоль цепочки распределяется продольная волна. Рассмотрим мгновенную фотографию расположения атомов.

И так рассмотрим линейную цепочку из одинаковых атомов с массами m , отклоненных от равновесных узлов с номерами (n – 1), n, (n + 1) на величины и_п-1 > 0, и_п > 0, и_п+1 < 0. В одномерном случае будем учитывать взаимодействие только ближайших (соседних) атомов, что не отражается существенным образом на результатах. Отклонения и_п и силы, действующие на атомы, считаются положительными, если их направления совпадают с направлением положительной оси и отрицательными – в противоположном случае.[3]

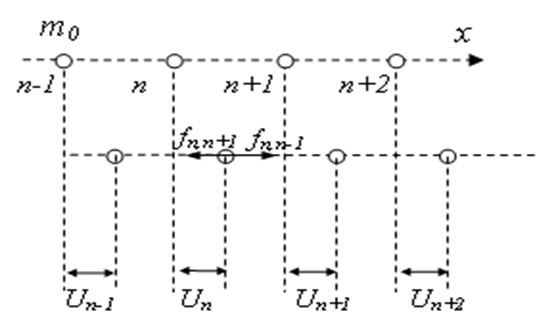
Рисунок 2.Фотография расположения атомов продольной волны

 

При малых отклонениях атомов от положений равновесия (|u|<<а – расстояние между узлами), силы взаимодействия можно рассматривать как квазиупругие, т. е. пропорциональные изменению расстояния между атомами. Таким образом, силы, действующие на n-й атом со стороны (n – 1)-го и (n + 1)-ro атомов, равны:

 

f_n,n-1= – β(и_п – и_п-1) и f_n,n+1= – β(и_п – и_п+1), (1.1.1)

 

где β>0 – коэффициент квазиупругой силы.

Результирующая сила, действующая на n-й атом,

 

f_n = f_n,n-1 + f_n,n+1= – β(2и_п – и_п-1 – и_п+1). (1.1.2)

 

Воспользуемся вторым законом Ньютона:

 

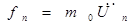 (1.1.3)

Объединяя (1.1.2) и (6), получим:

 

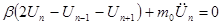 (1.1.4)

 

(1.1.4) – уравнение движения отдельного атома,

где

 

. (1.1.5)

 

Выражение для силы f_n может быть получено и другим путем. Потенциальная энергия решетки Ф есть функция от отклонений атомов и_п. Разлагая Ф в ряд по степеням малых отклонений и_п, получим

 

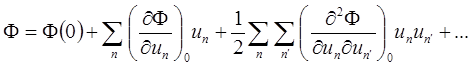, (1.1.6)

 

где индекс 0 указывает, что все и_п положены равными нулю. Не ограничивая общности, полагаем потенциальную энергию основного состояния Ф(0) = 0.

Так как значение и_п = 0 соответствует равновесию системы, то

 

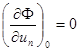. (1.1.7)

 

Для бесконечной атомной цепочки коэффициенты

 

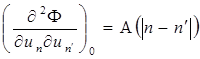, (1.1.8)

т. е. зависят только от расстояния между n-м и п'-м узлами. По определению сила

 

f_n= 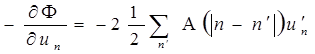. (1.1.9)

 

Если все и_п' = const = u₀, то сила

 

f_n = 0 = 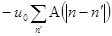, (1.1.10)

 

где и пробегает все значения. Если учитывать только ближайших к атому п соседей, то п' = п, n+ 1, n—1, и мы получим А(0) + А(1) + А(-1) = 0. Видно, что (1.1.9) дает тоже выражение для силы f_n что и (1.1.3), если положить А(1) = - 1/2A(O) = β [6].

Решение уравнения (1.1.3) представляет сложность, но бесконечная атомная цепочка с квазиупруго взаимодействующими атомами напоминает натянутую струну. Известно, что для бесконечной струны существует простой тип движения в виде бегущей монохроматической волны, для которой отклонение и струны от положения равновесия в точках х в момент t будет:

 

и(х, t) = Asin2π(x/λ – vt), (1.1.11)

 

где А — амплитуда, λ—длина волны и v—частота. Вводя циклическую частоту ω = 2πν и волновое число q = 2π/λ, получим

 

и (х, t) = A sin (qx—ωt). (1.1.12)

Если мы условимся рассматривать не только положительные, но и отри-цательные значения q, то наряду с волной, распространяющейся вдоль положительной оси x (q > 0), получим волны, бегущие в противоположном направлении (q < 0). Если учтем, что уравнение колебания струны линейно, так что сумма решений является также интегралом уравнения, то во многих случаях представляется математически более удобным пользоваться комплексной формой решения в виде

 

и(х, t) = Ae^i(qx-ωt), ( 1.1.13)

 

где амплитуда А может быть комплексным числом.

Систему (1.1.3) решим посредством подстановки

 

u_n = Ae^i(qan-ωt), (1.1.14)

 

где а – расстояние между узлами. Подставив (1.1.14) в (1.1.3) получим

 

ω²=2β/m(1-cosqa) или ω=ω_{m 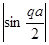,} (1.1.15)

 

где ω_m=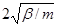

Решения (1.1.14) типа бегущей волны удовлетворяют уравнениям (1.1.3) для любого п, если частота ω связана с волновым числом q (или длиной волны λ) соотношением дисперсии (1.1.15)[2].

 

Дисперсия частот атомных колебаний

 

Для цепочки атомов, в отличии от однородной струны, имеет место дисперсия волн, т. е. частота ω зависит от волнового числа q[1]. На рисунке (3) показаны дисперсионные кривые ω(q) для однородной цепочки атомов.

Из условия

 

q_{max 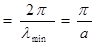,} (1.2.16)

 

имеем, что минимальная длина волны для выбранной цепочки атомов равна λ_min= 2a. При такой длине волны соседние атомы имеют равные 1и противоположно направленные амплитуды. В длинноволновом пределе q → 0, когда выполняется условие

 

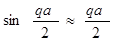, (1.2.17)

 

получим:

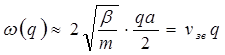. (1.2.18)

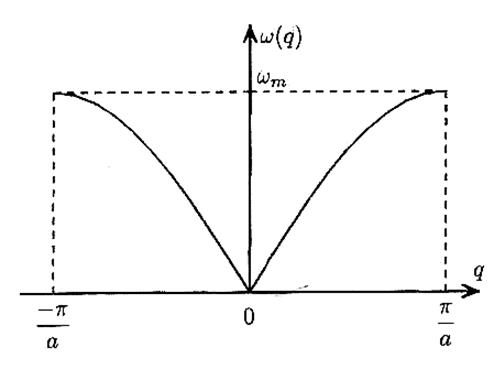
Рисунок 3. Дисперсионные кривые ω(q) для однородной цепочки атомов.

Колебания в данном случае можно рассматривать как колебания упругого континуума. Здесь ν_зв – скорость звука [2].

Формула (1.2.18) в предположении, что среда является непрерывной (континуум). Для нашей линейной цепочки нельзя считать среду непрерывной. Она является дискретной. Для дискретной среды наблюдается отклонение от линейности (1.2.18). Данное отклонение называется дисперсией, а полученные кривые (рис. 3) называются дисперсионными. Причина дисперсии – дискретность среды. Для дискретной среды существуют максимальные частоты, которые соответствуют минимальным длинам волн:

 

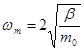 (1.2.19)

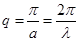 [3] (1.2.20)

 

Когда имеет место дисперсия ω(q), следует различать фазовую скорость v_ф, с которой распространяется фаза монохроматической волны и групповую скорость v_гр, с которой распространяется волновой пакет, построенный из волн с 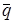, близким некоторому значению. Групповая скорость является скоростью переноса пакетом энергии из мест нарушения равновесия[2].

Вычислим значение фазовой и групповой скорости в нашем случае .

1. V_f – скорость распространения фазы (фазовая скорость):

 

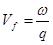 (1.2.21)

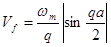 (1.2.22)

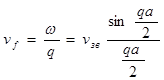, (1.2.23)

 

Назначаем значение данной скорости в длинноволновом пределе:

 

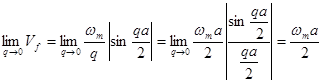 (1.2.24)

 

2. V_g – скорость передачи энергии; скорость перемещения горба волнового пакета (групповая скорость):

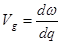 (1.2.25)

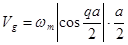 (1.2.26)

 

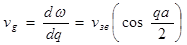 (1.2.27)

 

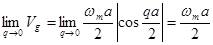 (1.2.28)

 

Сопоставление дает, что и фазовая и групповая скорость в длинноволновой области совпадают и равны скорости звука.

 

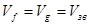 (1.2.29)

Вычислим, используя значения V_g на границе зоны Бриллюэна (интервал значений волнового числа 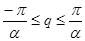 является по существу зоной Бриллюэна):

 

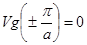 (1.2.30)

 

Это означает, что распространение продольной волны с 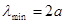 для цепочки конечных размеров образуется стоячая волна, а в случае стоячих волн передача энергии отсутствует и V_g=0.

Отметим, что все физические эффекты, наблюдаемые для простой одномерной цепочки, наблюдаются и для трехмерных кристаллов.