Найти множество Парето следующей двухкритериальной задачи.

Набор задач №34.

1. Построить математическую модель следующей  задачи оптимального планирования объемов производства.

 Компания производит погрузчики и тележки. От одного погрузчика компания получает доход в размере $80 и от одной тележки в размере $40 . Имеется три обрабатывающих центра, на которых выполняются операции металлообработки, сварки и сборки, необходимые для производства любого из продуктов. Для интервала планирования, равного месяцу, задана предельная производственная мощность каждого обрабатывающего центра в часах, а также количество часов, необходимое на этом центре для производства одного погрузчика и одной тележки. Эта информация задана в таблице.

 

	Погрузчик         Тележка (часы/ед.)         (часы/ед.)	Общ. мощ. (часы)
Мет. обраб. Сварка Сборка	6                           4 2                      3 9                           3	2400 1500 2700

 

Требуется составить допустимый план работ на месяц с максимальным доходом.

 

 

Решение.

Пусть  —  количество производимых погрузчиков;

         — количество производимых тележек.

         

 

Тогда целевая функция, обозначающая общую сумму  дохода по всем видам производимой продукции ( погрузчики и тележки ), равна

 

 

Задача состоит в нахождении допустимых значений переменных  и , максимизирующих J(x). При этом, в силу условия задачи, должны выполняться следующие ограничения на переменные:

 

для каждого из обрабатывающих центров время, затраченное на производство  и  единиц погрузчиков и тележек соответственно, не должно превышать предельной производственной мощности :

 

1)   часов в месяц ( для центра металлообработки)   ;

2)  часов в месяц ( для центра сварки) ;

3) 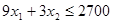 часов в месяц ( для центра сборки);

4)  (ограничение на неотрицательность переменных) .

 

Итак,  получили следующую математическую модель данной задачи:

 

 

 

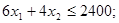
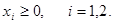
Найти множество Парето следующей двухкритериальной задачи.

 

, ,

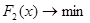при условии . Значения функций      заданы таблицей

 

x	1	2	3	4	5	6	7
	-2	-4	-6	-4	-6	-8	-6
	12	12	12	10	10	10	6

                                                                                 

 

 Решение.

 

Решим вопрос нахождения множества Парето данной задачи геометрически. Для этого изобразим на графике множество, состоящее из точек  

 

=  

 

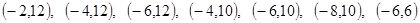
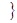
С помощью графика найдем все точки с максимальным значением координаты . В данном случае это одна точка, имеющая координаты (-2,12). Она войдет во множество оптимальных по Парето исходов. Далее исключим из рассмотрения все точки, координаты  которых не превосходят, а координаты  больше или равны координатам  найденной точки (-2,12) ( это (-4,12) и (-6,12) ). Снова из оставшихся точек выберем все с наибольшим значением . Это точка с координатами (-4,10). Из оставшихся две точки (-6,10) и (-8,10) нам не подходят, поскольку их координаты 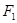  меньше первой координаты выбранной точки (-4,10), а координаты  равны второй координате этой точки. Значит, соответствующие им стратегии являются доминируемыми. Что же касается точки (-6, 6), то она  войдет во множество оптимальных по Парето точек. Окончательно  получили, что множество Парето данной задачи состоит из трех точек - (-2,12), (-4,10), (-6, 6). Они отвечают стратегиям под номерами 1, 4 и 7 соответственно. Таким образом, .

 

 

3. Геометрически решить задачу линейного программирования:

                                     ,

                            

 

        

Решение.

1. Строим область допустимых решений, т.е. геометрическое место точек, в котором одновременно удовлетворяются все ограничения данной ЗЛП. Каждое из неравенств  системы ограничений нашей задачи геометрически в системе координат ( , ) определяет полуплоскость соответственно с граничными прямыми.

Первому ограничению соответствует прямая, пересекающая координатные оси в точках с координатами ( 0, 6 ) и ( 6, 0 ).

Второму ограничению соответствует прямая, пересекающая координатные оси в точках с координатами ( 0, -1 ) и ( 1, 0 ).

Третьему ограничению соответствует прямая, пересекающая координатные оси в точке с координатами ( 1, 0 ) и проходящая параллельно оси .

Четвертому ограничению соответствует прямая, пересекающая координатные оси в точках с координатами ( 0, 6 ) и ( 3, 0 ).

Пятому ограничению соответствует прямая, пересекающая координатные оси в точках с координатами ( 0, 4 ) и ( -8, 0 ).

Шестому ограничению соответствует прямая, пересекающая координатные оси в точке с координатами ( 0, 1 ) и проходящая параллельно оси .

 

Области, в которых выполняются соответствующие ограничения в виде неравенств, указаны на рисунке стрелками, направленными в сторону допустимых значений переменных.

Полученная область допустимых решений выделена на рисунке серым цветом.

 

2. Вектор градиента  v  определяется координатами ( 0.5, 2 ). Он перпендикулярен линиям уровня и  указывает направление возрастания целевой функции. На рисунке красным цветом изображены линии уровня , заданные уравнениями  и 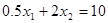, т. е. когда целевая функция принимает значение 0  и 10 соответственно.

 

 

3. По графику видно, что касание линии уровня ( ее уравнение 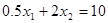), перед выходом из области допустимых решений, произойдет в точке пересечения прямых  и . Нетрудно подсчитать, что эта точка имеет координаты .

  

4. В этой точке  значение  целевой  функции будет наибольшим, т.е.

  .

 

 

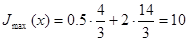4. Перейти к задаче  с ограничениями :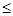

             

            

Решение.

 

Для начала попытаемся выразить одни переменные системы через определенный набор других переменных. С этой целью будем рассматривать расширенную матрицу системы ограничений и путем элементарных преобразований этой матрицы, выделим в ней единичную подматрицу :

 

 

 

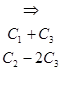
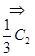
Воспользуемся последней расширенной матрицей и  выразимпеременные ,  и   через оставшиеся переменные  и . Помня, что , получаем новые ограничения :

 

 

Подставив эти значения вместо переменных 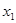,  и 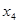  в  исходную задачу, для целевой функции получим:

 

 

Итак,  преобразовав полученные неравенства и целевую функцию, имеем задачу, эквивалентную исходной с ограничениями   « = » , но уже с ограничениями   «  »:

 

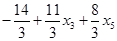
min,