Метод корневого годографа

Корневой годограф – геометрическое место точек корней характеристического уравнения замкнутой системы при изменении какого-либо параметра системы (чаще всего 0 £ к £ ¥).

Пусть задана передаточная функция разомкнутой системы

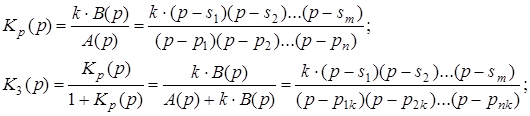 (6)

где s_i - нули передаточной функции разомкнутой системы;

p_i - полюса передаточной функции разомкнутой системы;

p_k - полюса передаточной функции замкнутой системы.

Задача состоит в том, чтобы, зная расположение нулей и полюсов передаточной функции разомкнутой системы, найти корни передаточной функции замкнутой системы как функции параметра системы. Это и есть корневой годограф.

Если полюс p_k (рис. 10) является корнем характеристического уравнения (т.е. точка принадлежит корневому годографу), то он обращает его в нуль, при этом выполняется условие модуля и аргумента:

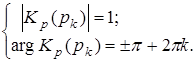
Для упрощения процедуры построения корневого годографа необходимо использовать правила, позволяющие приближенно определить расположение ветвей корневого годографа.

Рассмотрим основные свойства корневого годографа.

1. Число ветвей корневого годографа равно – n.

2. Ветви корневого годографа расположены симметрично вещественной оси и нигде не пересекаются.

3. Ветви корневого годографа начинаются в полюсах передаточной функции разомкнутой системы, заканчиваются в нулях, а т. к. n ³ m, то остальные n – m ветвей уходят в бесконечность.

4. Ветви корневого годографа уходят в бесконечность вдоль асимптот.

Точка пересечения асимптот определяется как центр тяжести координат нулей и полюсов

 (7)

Угол наклона асимптот определяется по формуле

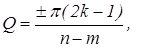
где к = 1,2,…,¥. (8)

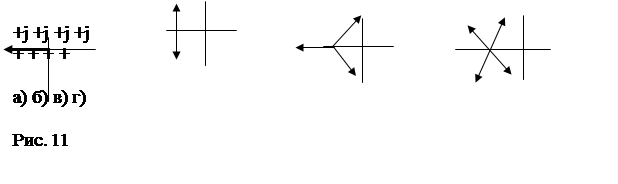
Например: угол наклона асимптот при различном их количестве имеет вид (рис. 11а-г)

при n-m = 1;  при n-m = 2;

при n-m = 3;  при n-m = 4;

Определим расположение ветвей корневого годографа в области двух полюсов, расположенных на вещественной оси (см. рис. 12).

p²+ap+b=0,  (9)

Если в-увеличивается, то значение подкоренного выражения уменьшается и корни сближаются. Если значение подкоренного выражения равно нулю, корни сольются. Если значение подкоренного выражения меньше нуля, корни станут комплексными.

Расположение ветвей корневого годографа в области двух нулей на вещественной оси приведено на рис. 12б.

Полюса движутся навстречу друг к другу, сливаются и далее расходятся к нулям.

Рис. 12

Рассмотрим примеры.