Способ вращения вокруг линии уровня

Действенным и наиболее рациональным приемом решения задач, в которых требуется определить натуральную величину угла, является способ вращения вокруг линии уровня.

Основные правила построения

1. Радиус вращения точки равен расстоянию между точкой и линией уровня, выполняющей роль оси. Натуральную величину радиуса определяют методом прямоугольного треугольника.

2. При вращении вокруг горизонтали h точка перемещается по окружности, которая проецируется на горизонтальную плоскость в отрезок прямой, перпендикулярный горизонтальной проекции горизонтали h'. На фронтальную плоскость окружность, по которой движется точка, проецируется в эллипс. Строить его нет необходимости.

3. При вращении вокруг фронтали f точка перемещается по окружности, которая проецируется на фронтальную плоскость в отрезок прямой, перпендикулярный фронтальной проекции фронтали f''. Вместе с тем горизонтальная проекция линии перемещения представляет собой эллипс, строить который не обязательно.

Рассмотрим, как определить действительную величину угла между прямыми a и b, пересекающимися в точке A. Построения представлены на рисунке и выполнены согласно алгоритму, который описан ниже.

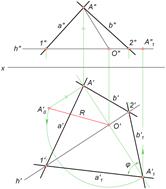
Алгоритм решения

1. Проводим фронтальную проекцию h'' горизонтали h. Она пересекает прямые a'' и b'' в точках 1'' и 2''. Определяем горизонтальные проекции 1' и 2' и через них проводим h'.

2. Находим центр вращения O. Его горизонтальная проекция O' лежит на пересечении прямой h' с перпендикуляром, проведенным из A' к h'.

3. Определяем натуральную величину радиуса вращения R = O'A'₀. Для этого строим прямоугольный треугольник O'A'A'₀, катет которого A'A'₀ равен расстоянию от A'' до h''.

4. Проводим дугу окружности радиусом R до пересечения её с прямой O'A' в точке A'₁. Соединяем A'₁ с точками 1' и 2'. Искомый угол ϕ построен.

 

Задача №1

Перевести прямую общего положения - в частное, т.е. чтобы прямая общего положения после поворота оказалась параллельной одной из плоскостей проекций. Прямую АВ (рис. 4-46) поставить в положение фронтали.

Рис. 4-46

Чтобы прямую АВ (рис 4-47 а) поставить в положение фронтали, необходимо установить А₁В₁ ^линиям связи (А₁В₁ ^ А₁А ₂)

Алгоритм(рис. 4-47)

1. Выбираем ось вращения i ^ П₁; i É А (рис. 4-47б)

2. Радиус вращения: R = | А В |.

3. Вращаем А₁В₁ вокруг оси i₁ = А₁ до положения, когда А₁В₁ станет ^ А₁А₂. (рис. 4-47в)

4. Точка А₂ останется на оси i₂, все другие точки прямой переместятся по прямым, перпендикулярным линиям связи. Точка В₂ переместится в положение В₂’.

5. Отрезок АВ’ - фронталь Þ | АВ | = |А₂В₂’| (рис. 4-47г)

6. Угол a - угол наклона АВ к П₁.

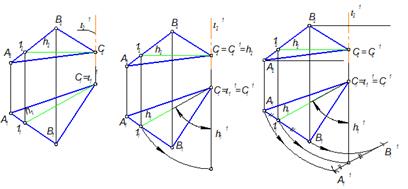
а) AB – прямая общего положения

б) i ^ П1

в) Прямая AB заняла положение фронтали

г) AB(AB’) - фронталь

Рис. 4-47

Задача №2

Прямую общего положения СD поставить в положение проецирующей прямой.

Алгоритм

1. Одним простым вращением нельзя прямую общего положения поставить в положение проецирующей, поэтому сначала решают задачу №1: прямую СD поставить в положение горизонтали.

2. Выбираем ось вращения i ^ П₂; i É С (рис. 4-48, б)

3. Радиус вращения: R = | С₂D₂ |

4. Вращаем C₂D₂ вокруг оси i₂ = C₂ до положения, когда C₂D₂ станет ^ C₁C₂ (рис. 4-48 в).

5. Точка C₁ останется на оси i₁, все другие точки прямой переместятся по прямым, перпендикулярным линиям связи. Точка D₁ переместится в положение D₁’

6. Отрезок CD’ - горизонталь Þ | CD | = | C₁D₁’ | (рис. 4-48, г)

7. Угол b - угол наклона CD к П₂.

а) CD – прямая общего положения

б)

в) Прямая CD заняла положение горизонтали

г) CD(CD’) - горизонталь

Рис. 4-48

8. Проводим второе вращение. Ось i² выбираем ^ П₁, i ² É D¹; i₁² = D₁¹; i₂² || D₁¹D₂¹ (рис. 4-49а);

9. Радиус вращения: R = | C₁D₁¹ |.

10. Вращаем C₁D₁¹ до положения, когда C₁D₁¹ станет || линиям связи, и станет равной С₁²D₁¹(точка D₁¹ не вращается).

11. Точка С₂, двигаясь по прямой, займет положение D₂¹, т.е. С₂² = D₂¹ (рис. 4-49 в)

12. Отрезок С²D¹ - проецирующий, С²D¹ ^^ П₂ .

13. Общий вид решения показан на рис. 4-49 б.

 

 

Задача №3

Плоскость общего положения поставить в положение проецирующей, Г(АВС)^^ П₂

Алгоритм

Рассмотрим преобразование плоскости общего положения Г(АВС) во фронтально проецирующую (Г ^ П₂), но две плоскости ^ друг другу, если одна из них Г(АВС) содержит перпендикуляр к другой (П₂). Что это за прямая? Такой прямой для Г(АВС) может быть только горизонталь, занимающая фронтально проецирующее положение (задача № 27 в рабочей тетради). Значит в плоскости Г(АВС)нужно провести горизонталь и повернуть ее горизонтальную проекцию || линиям связи.

1. Проводим в плоскости горизонталь h (h₁ h₂) через точку С.

2. Выбираем положение ось i¹ ^ П₁, i¹ É С (рис. 4-50 а).

3. Поворачиваем горизонталь h вокруг оси пока она не займет положение h ^ П₂, т.е. h₁ || линиям связи, R^h = | C₁1₁ | (рис. 4-50 б)

4. Поворачиваем точки А и В в ту же самую сторону, на тот же самый угол, что и горизонталь, R^h = | С₁А₁ |, R^B = | С₁В₁ | (рис. 4-50 в).

5. Фронтальные проекции точек А(А₂) и В(В₂) перемещаются по прямым, линиям связи и занимают положение А₂¹ и В₂¹.

6. Плоскость Г займет фронтально проецирующее положение (Г₂¹ -вырождается в прямую линию) Þ Г₂¹ - главная проекция (рис.4-50 г).

7. Новое положение плоскости Г(Г₂¹) показано на (рис. 4-50 д).

Задача №4

Плоскость общего положения поставить в положение плоскости уровня, Г(АВС) || П₁

Алгоритм

1. Одним простым вращением нельзя плоскость общего положения поставить в положение плоскости уровня, поэтому сначала решаем задачу №3 (рис. 4-50).

2. Произведем второе вращение. Ось вращения i² ^^ П₂, i² É В¹ (рис. 4-51 а).

3. Поворачиваем Г₂¹ до положения, когда Г₂² станет ^ линиям связи (рис. 4-51 б).

4. Точки А₁¹, С₁¹ переместятся по прямым до положения А₁², С₁².

5. Плоскость Г² -плоскость уровня Þ Г₂² - ее главная проекция, Г₁² - натуральная величина DАВС.

 

18. Способ плоскопараллельного перемещения. Решение четырёх основных задач преобразования комплексного чертежа способом плоскопараллельного перемещения.

Плоско-параллельным перемещением называется такое движение объекта, при котором все его точки перемещаются в плоскостях , параллельных между собой.

При плоскопараллельном перемещении относительно горизонтальной плоскости проекций П₁ все точки объекта перемещаются в горизонтальных плоскостях уровня. При этом горизонтальная проекция объекта по форме и размерам не меняется, изменяется только положение объекта относительно плоскости П₁. Фронтальные проекции точек объекта перемещаются по прямым, параллельным оси проекций х.

При плоскопараллельном перемещении относительно фронтальной плоскости проекций П₂ все точки объекта перемещаются во фронтальных плоскостях уровня при этом фронтальная проекция объекта по форме и размерам не меняется, изменяется только положение объекта относительно плоскости П₂. Горизонтальные проекции точек объекта перемещаются по прямым, параллельным оси проекции х (рисунок 1.4.8).

Рисунок 1.4.8 – Плоско-параллельное перемещение

Рассмотрим примеры преобразования чертежа способом плоскопараллельного перемещения при графическом решении четырех основных задач.

Задача №1. Преобразовать прямую общего положения во фронтальную прямую уровня (рисунок 1.4.9).

Решение. Выполним плоско-параллельное перемещение прямой АВ относительно фронтальной плоскости проекций. Для того, чтобы прямая стала параллельной П₂, горизонтальную проекцию (АВ) А₁В₁ переместим в свободное место чертежа и расположим параллельно оси х. При этом длина отрезка А₁В₁=А₁¹В₁¹. Фронтальные проекции точек АВ (А₁В₁) перемещаются соответственно по прямым α₂, β₂ – фронтальным проекциям горизонтальных плоскостей уровня α и β, в которых перемещаются точки А и В. Затем перпендикулярно оси х из проекций точек А₁¹и В₁¹ проведем линии связи. Из проекций А₂ и В₂ параллельно оси х проведем линии связи до пересечения с соответствующими линиями связи в соответствии с рисунком 1.4.9. В результате построения определяется натуральная величина АВ и угол γ его наклона к горизонтальной плоскости проекций.

Рисунок 1.4.9 – Решение первой основной задачи способом плоско-параллельного перемещения

Задача №2. Преобразовать прямую общего положения в горизонтально-проецирующую прямую (рисунок 1.4.10).

Решение. Эта задача решается при помощи двух преобразований. Сначала прямую АВ преобразуем во фронтальную прямую уровня (смотри задачу №1), а затем плоскопараллельно переместим прямую АВ относительно фронтальной плоскости проекций и преобразуем в горизонтально проецирующую прямую. Для этого проекцию прямой АВ( А₂¹В₂¹) переместим в свободное место чертежа и расположим ее перпендикулярно оси х, не изменяя ее размеров. При этом горизонтальные проекции точек отрезка прямой АВ(А₁¹В₁¹) перемещаются по прямой θ₁- горизонтальной проекции фронтальной плоскости уровня θ, в которой перемещаются точки АВ. Определим точку пересечения линий связи проекций точек А₁¹ ,В₁¹ и А₂¹ ,В₂¹. Горизонтальная проекция преобразованной прямой проецируется в точку, т.е. прямая АВ преобразилась в горизонтально проецирующую прямую.

Рисунок 1.4.10 – Решение второй основной задачи способом плоско-параллельного перемещения

Задача №3. Преобразовать плоскость общего положения во фронтально проецирующую плоскость (Рисунок 1.4.11).

Решение. Плоскость задана треугольником ABC. В плоскости треугольника предварительно построим фронталь f(f₁,f₂). Заметим, если плоскость преобразуется в горизонтально проецирующую, то в плоскости проводиться горизонталь h. Треугольник плоскопараллельно перемещаем таким образом, чтобы фронталь треугольника располагалась перпендикулярно горизонтальной плоскости проекций, то сама фронталь на эту плоскость проецируется в точку, а плоскость треугольника – в прямую, т.е. плоскость треугольника ABC станет горизонтально проецирующей. Поэтому в свободном месте чертежа фронтальную проекцию ΔABC(A₂B₂C₂) расположим так, чтобы фронтальная проекция фронтали (f₂) располагалась перпендикулярно оси х. При этом фронтальные проекции треугольника не изменили своей формы (A₂B₂C₂= A₂¹B₂¹C₂¹), а горизонтальные проекции вершин ΔABC(A₁B₁C₁) переместились по прямым α₁, β₁, γ₁ – горизонтальным проекциям фронтальных плоскостей уровня, проведенных через эти вершины. Фронтальная проекция Δ ABC (A₁¹B₁¹C₁¹) будет представлять собой отрезок прямой, т.е. плоскость треугольника станет горизонтально проецирующей. При помощи этой задачи также определяется натуральная величина угла наклона φ плоскости Δ ABC к фронтальной плоскости проекций (рисунок 1.4.11).

Рисунок 1.4.11 - Решение третьей основной задачи способом плоско-параллельного перемещения

Рисунок 1.4.12 - Решение четвертой основной задачи способом плоско-параллельного перемещения

Задача №4. Преобразовать плоскость общего положения во фронтальную плоскость уровня (рисунок 1.4.12).

Решение. Для решения этой задачи необходимо выполнить два преобразования: сначала преобразовать плоскость треугольника во фронтально проецирующую плоскость (смотри задачу №3), а затем преобразовать Δ ABC, чтобы он находился во фронтальной плоскости уровня. Для этого на свободном месте чертежа расположим горизонтальную проекцию Δ ABC(A₁¹B₁¹C₁¹) параллельно оси х. При этом A₁B₁C₁=A₁¹B₁¹C₁¹, а фронтальные проекции вершин треугольника будут перемещаться по соответствующим плоскостям уровня – λ₂, κ₂, τ₂. Так как преобразованный треугольник лежит в плоскости уровня, следовательно, его фронтальная проекция после последнего преобразования, будет являться натуральной величиной Δ ABC.

 

19. Преобразование чертежа способом вращения вокруг линии уровня.

 

20. Многогранник, классификация, принадлежность точки и линии поверхности многогранника.

Поверхность, образованная частями попарно-пересекающихся плоскостей- многогранная. Элементами многогранной поверхности являются грани, ребра, вершины.

Отсеки плоскостей, образующие многогранную поверхность- грани, линии пересечения смежными гранями- ребрами, точки пересечения не менее 3 граней- вершины.

Многогранная поверхность называется пирамидальной, если все ее ребра пересекаются в одной точке, называемой вершиной.

Многогранная поверхность называется призматической, если все ее ребра параллельны между собой.

Совокупность всех ребер и вершин многогранника- сетка.

Правильные многогранники (тела Платона):

тетраэдр(4 грани)

октаэдр(8 граней)

додекаэдр(12 граней)

икосаэдр(20 граней)

вокруг всех правильных многогранников можно описать сферу.

Принадлежность точки и линии поверхности многогранника.

Построение любых проекций точек на поверхности многогранника осуществляется наиболее эффективно при помощи образующих и направляющих, хотя можно использовать и другие приемы.

Как правило, задача формулируется следующим образом: по двум проекциям многогранника построить третью и начертить недостающие проекции точки или линии на его поверхности.

Линию на поверхности многогранника можно построить по характерным точкам, которыми являются точки ее изгиба и точки перехода через ребра. При этом следует помнить, что ломаная линия на поверхности многогранника будет ломаной, состоящей из отрезков прямой , в любой плоскости проекций, а кривая – кривой ( за исключением частных случаев).

21. Пересечение многогранников плоскостью частного положения.

Cечение — изображение фигуры, полученной в секущей плоскости. Способ ребер подразумевает определение точек пересечение ребер с заданной плоскостью. Способ граней определяет линии пересечения граней многогранника с заданной плоскостью.

 

22. Пересечение кривых поверхностей. Метод плоских посредников.

Для определения линии пересечения двух произвольных поверхностей вращения целесообразно воспользоваться одним свойством, присущим поверхностям вращения, которое состоит в том, что две любые соосные поверхности вращения пересекаются по окружностям, проходящим через точки пересечения меридианов поверхностей.

 

В частном случае, если одна из поверхностей вращения – сфера, приведенное выше предложение может быть сформулировано иначе: если центр секущей сферы находится на оси поверхности вращения, то сфера пересечет данную поверхность по окружностям, число которых равно числу точек пересечения главных меридианов поверхностей.

 

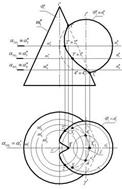
Задача: построить линию пересечения двух поверхностей вращения: конуса (Φ₁) и сферы (Φ₂). Графическое оформление задачи приведено на рис. 7.

 

Рис. 7

 

Символическая запись условия задачи: Φ₁, Φ₂; Φ₁ ∩ Φ₂ = ℓ ?

Анализ и решение задачи:

1) пересекаются две поверхности вращения второго порядка, следовательно, линия пересечения ℓ является кривой четвертого порядка.

2) так как вид пересечения – «врезка» (несквозное пересечение), то получается одна линия пересечения ℓ.

3) поверхности имеют общую плоскость симметрии α₁, параллельную фронтальной плоскости проекций, значит пересечение их фронтальных очерков дает пару характерных точек – верхнюю и - нижнюю.

4) в качестве посредников для последующих построений в этой задаче целесообразно принимать горизонтальные плоскости α₂, α₃ и т. д., поскольку линии пересечения ими каждой из поверхностей являются наипростейшими (окружностями).

5) границей зоны видимости искомой кривой ℓ для горизонтальной плоскости проекций является экватор сферы, поэтому плоскость – посредник α₂ проведенная через экватор сферы Φ₂, дает на втором шаге алгоритма принадлежащие экватору точки 2 и , являющиеся границами зоны видимости для горизонтальной плоскости проекций. Эти же точки являются самыми левыми.

6) границами видимости для фронтальной плоскости проекций являются главные фронтальные меридианы и принадлежащие им точки 1 и .

Таким образом, построение линии пересечения поверхностей сводится к следующему.

Во-первых, проводим плоскость α₁, параллельную фронтальной плоскости проекций через оси i и ј поверхностей. На горизонтальной плоскости проекций – это след-проекция , параллельная оси х. На фронтальной проекции находим точки пересечения очерков . Сносим полученные точки на горизонтальный след-проекцию плоскости α₁ с учетом видимости (точка ^' – видимая, – невидимая). Записываем первый шаг алгоритма в виде:

1)

где точка 1 – верхняя, точка - нижняя.

Отметим, что алгоритм записывается для пространства, а построение проекций точек и линии ℓ производится для каждой плоскости проекций с обязательным обозначением всех элементов построения.

Во-вторых, через экватор сферы Φ₂ проводим плоскость-посредник α₂, параллельную горизонтальной плоскости проекций (см. ). Параллели m₂ и n₂фронтальной проекции неразличимы, так как их проекции m₂^" и n₂^" частично накладываются друг на друга. Поэтому строим их горизонтальные проекции m₂^' и n₂^', как окружности соответствующих радиусов и точки их пересечения. Фронтальные проекции ^" этих точек находим на след-проекции плоскости α₂ по линиям проекционной связи. Записываем второй шаг алгоритма:

2)

точка 2 – левая ближняя, точка - левая дальняя. Обе точки – границы видимости.

В-третьих, произвольно проводим плоскость α₃, параллельную плоскости . Аналогично второму шагу, находим горизонтальные проекции линий пересечения этой плоскости с каждой поверхностью и горизонтальные проекции точек , а затем на следе-проекции – фронтальные проекции этих точек. Записываем третий шаг алгоритма:

3) - произвольные точки. Аналогично можно было бы получить точки под номерами 4, 5 и т. д., но для данной задачи в этом нет необходимости, так как характер и форма кривой определены достаточно полно.

В-четвертых, соединяем полученные точки между собой. Поскольку искомая кривая ℓ является замкнутой, ее построение можно начинать с любой точки и в любом направлении, например .

Заключительный этап алгоритма может быть записан в виде:

 

ℓ = или ℓ = .

 

23. Пересечение кривых поверхностей. Метод концентрических, сферических посредников.

Метод концентрических сферических посредников является уникальным способом, так как позволяет решать задачи в одной проекции. Сущность этого способа заключается в том, что две поверхности вращения с общей осью пересекаются по окружностям, которые на плоскости проекций, параллельной оси вращения, изображаются отрезками прямых линий, проходящих через точки пересечения очерков поверхностей. Так, например, пересечение цилиндрической поверхности и одной полы конической поверхности происходит по окружности q. Пересечение сферы с поверхностью вращения происходит также по окружностям, если центр сферы лежит на оси поверхности вращения. Таким образом, если заданы две поверхности вращения с пересекающимися осями, то сфера с центром в точке пересечения осей пересекает заданные поверхности по окружностям. Если оси поверхностей параллельны плоскости проекций, то плоскости получаемых окружностей перпендикулярны к этой плоскости проекций и изображаются в виде отрезков прямых линий. Окружности, получаемые в пересечении сферы с одной и другой поверхностью, пересекаются между собой в двух точках. В проекции, параллельной общей плоскости симметрии поверхностей, точки пересечения попарно сливаются в одну.

Для построения точек линии пересечения проводится несколько сфер различного радиуса. Вспомогательная сфера, касательная к цилиндру, не пересекается с конусом, а значит, не может быть использована для построений. Вспомогательная сфера, касательная к конусу, пересекается с цилиндром по двум окружностям и является сферой минимального радиуса пригодной для построений. Из точки пересечения осей опустим перпендикуляр на образующую конуса и этим радиусом проведем фронтальный очерк сферы. Через точку основания перпендикуляра проходит окружность касания сферы с конусом, которая изображается отрезком прямой линии, перпендикулярной к оси конуса. Через точки пересечения очерка сферы и цилиндра проходят окружности пересечения сферы с цилиндром, которые изображаются отрезками прямых линий, перпендикулярных к оси цилиндра. На пересечении проведенных отрезков (в пространстве окружностей) получаются общие точки поверхностей. Увеличивая радиус сферы, и повторяя этот прием несколько раз, можно получить множество точек линии пересечения. Очерки заданных поверхностей лежат в одной фронтальной плоскости, поэтому точки их пересечения также принадлежат линии пересечения. Вспомогательные сферы, имеющие радиус больше расстояния от центра сфер до этих точек, определяют мнимые точки пересечения. При пересечении поверхностей вращения меньшая поверхность врезается в большую поверхность. Для определения, какая именно поверхность больше, а какая меньше, сравнивают сферы касательные к заданным поверхностям.

 

Метод сфер используют для построения линии пересечения поверхностей вращения с пересекающими осями и общей плоскостью симметрии параллельной плоскости проекций, на которой выполняются построения.

 

24. Частные случаи пересечения поверхностей. Теорема Монжа.

Как правило, на практике имеют место частные случаи пересечения поверхностей, которые очень просты в построении, но их сложнее представить. Рассмотрим некоторые частные случаи пересечения поверхностей.

 

Известно, что порядок линии пересечения поверхностей равен произведению порядков поверхностей. При определенных условиях линия пересечения, в общем случае пространственная кривая линия, может распадаться на несколько линий более низкого порядка. При этом сумма порядков линий, на которые распадается алгебраическая кривая линия, равна порядку самой линии. Следует иметь ввиду, что некоторые линии, на которые распадается кривая, могут мнимыми линиями. Случаи, когда кривая четвертого порядка (линия пересечения двух поверхностей второго порядка) распадается на четыре прямые линии, можно проследить на примерах пересечения двух цилиндрических поверхностей второго порядка с параллельными образующими или двух конических поверхностей второго порядка с общей вершиной. Условия, при которых кривая четвертого порядка распадается на две кривые второго, могут быть сформулированы следующими теоремами:

1. Если две поверхности второго порядка пересекаются по одной плоской кривой, то они пересекаются еще по одной плоской кривой линии.

2. Если две поверхности второго порядка имеют касание в двух точках, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую линию, соединяющую точки касания.

3. Если две поверхности второго порядка описаны около третьей поверхности, то их линия пересечения может распадаться на две плоские кривые линии второго порядка, плоскости которых проходят через прямую линию, соединяющую точки пересечения линий касания.

Теорема Монжа

Если две поверхности второго порядка описаны около третьей или вписаны в нее, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую,

соединяющую точки пересечения линий касания.

 

25. Какое изображение называется главным видом и какие требования предъявляются к выбору главного вида на чертеже.

Изображение на фронтальной плоскости проекций (на грани 1) считается главным. Предмет располагают относительно фронтальной плоскости проекций так, чтобы изображение давало наиболее полное представление о форме и размерах предмета, несло наибольшую информацию о нем. Это изображение называют главным. В зависимости от своего содержания изображения предметов разделяют на виды, разрезы, сечения.

 

26. Перечислить основные виды и их расположение на чертеже в соответствии с ГОСТ 2.305.

Виды

Преимущественный метод изображения объемных изделий на плоскости — это ортогональное проецирование. Расположение изображаемого предмета предполагается между условным наблюдающим и проекционной плоскостью. Для повышения читаемости изображения разрешается применять упрощенный подход. Поэтому изображения на чертежах не являются проекционными в строгом геометрическом смысле этого слова. Их называют изображениями на плоскости. Для получения основных проекций, изображаемую деталь помещают в центре воображаемого куба. Грани его будут служить проекционными плоскостями.

Основные виды

В результате проекции образа предмета возникает схема основных видов изделия:

· спереди;

· справа;

· снизу;

· слева;

· сверху;

· сзади.

В техническом черчении вид спереди считается главным. Он должен давать максимум информации об изображаемой детали. Дополняют его виды слева и сверху (относительно главного). Эти три вида называют основными. Остальные считаются вспомогательными. Их изображения строят, если важная конструктивная информация об изделии сложной формы не видна на трех основных видах.

Кроме того, для пояснения строения части детали применяются местные виды, показывающие фрагмент изображения основного вида. Такие изображения размещают в незанятых областях, надписывая заглавными буквами кириллицы. На основном виде в зоне расположения фрагмента изображается стрелка, показывающая направление условного взгляда, в результате которого появляется местный вид. Такие рисунки ограничиваются линиями разрыва, проводимыми в направлении минимального размера элемента.

Кроме того, применяются дополнительные виды. Они строятся на плоскостях, размещенных под углом к основным граням проекционного куба. Они помогают проиллюстрировать расположение и строение тех участков объекта, которые не видны или недостаточно информативно представлены на основных видах, либо их габариты и конфигурация искажены. Обозначение дополнительных видов проводится литерами кириллического алфавита.

 

27. Что такое дополнительный вид.

Дополнительными называют виды, полученные проецированием на плоскости не параллельные основным плоскостям проекций. Их используют, когда необходимая для изображения часть предмета имеет наклон к основным плоскостям проекций.

Д ополнительный вид получается путем проецирования предмета или его части на дополнительную плоскость проекций (рисунок 2.4), не параллельную ни одной из основных плоскостей проекций. Такое изображение необходимо выполнять в том случае, когда какую-либо часть предмета невозможно изобразить без искажения формы или размеров на основных плоскостях проекций. Дополнительная плоскость проекций в этом случае может быть расположена перпендикулярно одной из основных плоскостей проекций.

Направление взгляда должно быть указано стрелкой, обозначенной той же прописной буквой украинского алфавита, что и в надписи над видом. Соотношение размеров стрелок, указывающих направление взгляда, должно соответствовать приведенным на рисунке 2.4.

Когда дополнительный вид расположен в непосредственной проекционной связи с соответствующим основным видом, обозначать его не нужно (рисунок 2.4, а). В остальных случаях дополнительный вид должен быть отмечен на чертеже надписью типа «А» (рисунок 2.4,б), а у связанного с дополнительным видом изображения нужно поставить стрелку, указывающую направление взгляда, с соответствующим буквенным обозначением.

Дополнительный вид можно повернуть до соосности с основным. При этом к надписи типа «А» необходимо добавить знак повернутого изображения (рисунок 2.4, в).

 

 

Рисунок 2.4 Дополнительные виды

 

28. Что такое местный вид.

Местный вид – изображение определенного ограниченного места поверхности предмета (малой части основного или дополнительного вида), как правило, ограничивается волнистой линией. Часто изображается в увеличенном масштабе. Если местный вид расположен в непосредственной проекционной связи с соответствующими изображениями, то его не обозначают (аналогично: основные и дополнительные виды).

В остальных случаях местные виды обозначаются подобно видам дополнительным, местный вид может быть ограничен линией обрыва: вид «Б» на рисунке 2.5. Виды «А» и «Б» на рисунке 2.5 изображают ограниченную часть вида, почему и являются местными.

В

Рисунок 2.5 Местные виды

ыполнены местные виды могут быть по-разному, и иногда их трудно четко отличить от дополнительных. Так на рисунке 2.6азадан на главном виде стрелкой и буквой вид «А», а на рисунке 2.6б вид «А» выполнен в увеличенном масштабе. На рисунке 2.6в вид «А» выполнен так же, но повернут до соосности с главным. На рисунках 2.6г и 2.6.двид «А» является дополнительным, только на рисунке 2.6.ддополни-тельный вид «А» повернут.

                                              Рисунок 2.6 Местные (б, в) и дополнительные (г, д) виды

 

 

29-30. Как классифицируют разрезы в зависимости от положения секущей плоскости относительно плоскостей проекции.

Как классифицируют разрезы в зависимости от числа и взаимного расположения секущих плоскостей.

а) пpостые- пpи одной секущей плоскости;

б) сложные- пpи нескольких секущих плоскостях.

В зависимости от положения секущей плоскости относительно гоpизонтальной плоскости пpоекций pазpезы pазделяются на:

а) гоpизонтальные- секущая плоскость паpаллельна гоpизонтальной плоскости пpоекций;

б) веpтикальные- секущая плоскость пеpпендикуляpна гоpизонтальной плоскости пpоекций;

в) наклонные- секущая плоскость составляет с гоpизонтальной плоскостью пpоекций угол, отличный от пpямого.

Веpтикальные pазpезы называются:

а) фpонтальными, если секущая плоскость паpаллельна фpонтальной плоскости пpоекций;

б) пpофильными, если секущая плоскость паpаллельна пpофильной плоскости пpоекций.

Сложные pазpезы pазделяются на:

а) ступенчатые, если секущие плоскости паpаллельны (ступенчатые гоpизонтальные, ступенчатые фpонтальные);

б) ломаные, если секущие плоскости пеpесекаются.

Pазpезы называются:

а) пpодольными, если секущие плоскости напpавлены вдоль длины или высоты пpедмета;

б) попеpечными, если секущие плоскости напpавлены пеpпендикуляpно длине или высоте пpедмета.

Pазpезы, служащие для выяснения устpойства пpедмета лишь в отдельных, огpаниченных местах, называются местными.

Пpостые pазpезы

Положение секущей плоскости не отмечают и pазpез надписью не сопpовождают, если одновpеменно выполняются тpи условия:

а) секущая плоскость совпадает с плоскостью симметpии пpедмета в целом;

б) pазpез pасположен в непосредственной пpоекционной связи с соответствующим изобpажени