Алгоритм Прима-Краскала

1. Инициализируем граф - вводим матрицу весов графа D[i,j]

2. "Раскрашиваем" вершины графа в разные цвета

3. До тех пор, пока число ребер остова меньше числа вершин графа, выполняем:

1) Находим ребро минимальной длины, не включенное до этого в остов графа и не образующее цикла с остовом

2) Включаем найденное ребро минимальной длины в остов

3) Меняем цвет всех вершин, входящих в остов, на один цвет

Докажем, что описанный алгоритм получает в точности минимальное решение.

Для доказательства нам понадобится очень простое утверждение:

Если к дереву добавить ребро, то в дереве появится цикл, содержащий это ребро.

Действительно, пусть добавлено ребро (u, v) – «добавлено» означает, что ребро – новое, что раньше его в дереве не было. Поскольку дерево является связным графом, то существует цепь С(u, ..., v) из нескольких ребер, соединяющая вершины u и v. Добавление ребра (u, v) замыкает цепь, превращая ее в цикл.

Теорема. Алгоритм Прима-Краскала получает минимальное остовное дерево.

Доказательство. Результатом работы алгоритма является набор из n-1 ребер. Они не образуют цикла, ибо на каждом из n-1 шагов соединялись вершины разного цвета, т. е. ранее не связанные. Этот граф связный, потому что после проведения 1-го ребра осталось n-1 разных цветов, ..., после проведения (n-1)-го ребра остался один цвет, т. е. одна компонента связности. Итак, полученный набор ребер образует связный граф без циклов, содержащий n-1 ребер, т. е. n вершин. Следовательно, граф есть остовное дерево.

Осталось доказать, что оно имеет минимальную длину. Пусть { } ребра остовного дерева в том порядке, как их выбирал алгоритм, т. е. . Предположим для простоты доказательства, что все ребра сети имеют разную длину, т.е.

                                      (2)

Если полученное дерево не минимально, то существует другое дерево, задаваемое набором из n-1 ребер { }, такое что сумма длин  меньше суммы длин . С точностью до обозначений

                                      (3)

Может быть, ,  и т.д., но так как деревья разные, то в последовательностях (2) и (3) найдется место, где ребра отличаются. Пусть самое левое такое место – k, так что  (k может равняться единице, это не испортит доказательства). Поскольку  выбиралось по алгоритму самым малым из необразующих цикла с .ребрами , то . Теперь добавим к дереву (3) ребро  в нем появится цикл, содержащий ребро  и, может быть, какие-то (или все) ребра из , но они сами не образуют цикла, поэтому в цикле будет обязательно ребро d из набора , причем 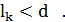 Выбросим из полученного графа с одним циклом ребро d; мы снова получим дерево, но оно будет на   короче минимального, что невозможно. Полученное противоречие доказывает теорему для сети со всеми разными ребрами.

Если не предполагать, что все ребра разные, то в доказательстве могло бы получиться, что , и нам пришлось бы двигаться дальше по последовательностям (2) и (3), пока бы мы не нашли 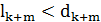. Это усложняет доказательство, но не меняет заключения.

В заключение анализа алгоритма оценим требуемую память и требуемое число операций. В варианте Прима надо хранить 2n координат точек, в варианте Краскала – n² расстояний; в обоих вариантах удобно хранить 2(n-1) номеров вершин, т е. n-1 ребер ответа. Всего требуется памяти 0(n ), т.е. порядка n², что, учитывая реальные величины n, необременительно. Для нахождения текущего минимального ребра надо просмотреть 0(n²) чисел и сделать это надо n-1 раз, так что временная сложность алгоритма 0(n³). Это тоже реально. Задача Прима-Краскала относится к просто и точно решаемым.