Алгоритм Прима-Краскала. Решение задач.

Пример 1. (вариант 17 контрольной работы по теме «Графы»)

Найти остовное дерево минимальной длины для графа, заданного следующей матрицей весов

Решение.

Изобразим граф, заданный таблицей весов:

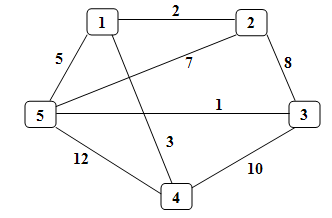
Воспользуемся алгоритмом Прима-Краскала (описание алгоритма на странице 14 курсового проекта).

1 шаг: Раскрашиваем вершины графа в разные цвета:

2 шаг: Находим ребро минимальной длины и включаем его в остов. Соединенные вершины остова перекрашиваем в один цвет:

 

3 шаг: Находим следующее ребро минимальной длины, не входящее в остов, и включаем его в остов. Все вершины, связанные с ребром, перекрашиваем в один цвет:

4 шаг: повторяем основной шаг:

5 шаг: повторяем основной шаг:

Все вершины графа связаны ребрами – мы получили искомый остов. Его матрица весов имеет вид:

 

На этом примере была также протестирована реализация алгоритма Прима-Краскала на языке Паскаль, приведенная в Приложении. Результаты тестирования совпадают с полученным нами решением:

 

Примечание: матрицу неориентированного графа достаточно задавать выше (ниже) ее главной диагонали.

 

Пример 2. Найти остовное дерево минимальной длины для следующего графа:

 

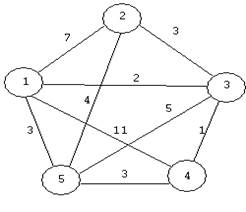
Искомое остовное дерево:

Результаты тестирования программы, приведенной в Приложении:

 

Пример 3. Случай вырожденного графа с пятью вершинами:

 

Заключение

Теория графов, будучи крупной ветвью комбинаторной математики, интенсивно изучалась в течение не одной сотни лет. Было выявлено много важных и полезных свойств графов, однако многие задачи еще ждут своего решения. Как и множество других предметных областей, которые приходилось изучать, алгоритмическое исследование графов возникло сравнительно недавно. И хотя некоторые фундаментальные алгоритмы открыты давно, все же большая часть интереснейших алгоритмов получена в течение нескольких последних десятилетий. Даже простейшие алгоритмы на графах позволяют получить полезные компьютерные программы, а нетривиальные алгоритмы относятся к числу наиболее элегантных и интересных из известных алгоритмов. Чтобы продемонстрировать все разнообразие приложений, использующих графы для обработки данных, рассмотрим нескольких примеров.

Географические карты. Путешественник, прежде чем отправиться в путь, желает получить ответ на вопросы типа: "Какой маршрут из Принстона в Сан-Хосе потребует наименьших расходов?' Пассажир, для которого время дороже денег, хотел бы получить от- ответ на такой вопрос: "Каким путем быстрее всего добраться из Принстона в Сан-Хосе?" Чтобы ответить на вопросы подобного рода, мы выполняем обработку информации, характеризующей соединения (пути следования) между элементами (городами и населенными пунктами).

Гипертекст. Когда мы просматриваем Web-каталоги, мы сталкиваемся с документами, содержащими различные ссылки (соединения) на другие документы, и переходим от документа к документу, щелкая мышью на этих ссылках. Сама по себе "всемирная паутина" представляет собой граф, в котором в качестве элементов выступают документы, а соединения суть связи. Алгоритмы обработки графов являются важными компонентами поисковых механизмов, которые помогают определить местоположение информации в Web.

Микросхемы. Микросхемы содержат такие элементы, как транзисторы, резисторы, конденсаторы, которые связаны между собой сложнейшим образом. Для управления машинами, изготавливающими микросхемы, и для проверки, выполняют ли эти цепи заданные функции, используются компьютеры. Мы хотим получить ответы на простые вопросы наподобие "Имеются ли в цепи условия для короткого замыкания?" и на более сложные вопросы, такие как "Можно ли скомпоновать микросхему на кристалле таким образом, чтобы шины не пересекались?". В данном случае, ответ на первый вопрос зависит только от свойств соединений (шин), в то время как для ответа на второй вопрос потребуется подробная информация о шинах, элементах, которые эти шины соединяют, и физических ограничениях, накладываемых кристаллом.

Составление расписаний. Производственный процесс требует решения различных задач под воздействием некоторого множества ограничений, по условиям которых решение одной задачи не может быть начато до тех пор, пока не будет завершено решение другой задачи. Мы представляем эти ограничения в виде соединений между этими задачами (элементами), при этом перед нами возникает задача составления расписаний (scheduling) в ее классическом виде: как построить временной график решения задач таким образом, чтобы удовлетворить заданным ограничениям и завершить данный процесс за минимально возможное время?

Транзакции. Телефонная компания поддерживает базу данных телефонного трафика. В этом случае соединения представляют телефонные вызовы. Мы заинтересованы в том, чтобы знать все, что касается характера структуры соединений, ибо хотим проложить провода и установить коммутаторы так, чтобы эффективно справляться с телефонным трафиком.

Еще одним примером может служить то, как финансовое учреждение отслеживает операции купли/продажи на рынке. Соединение в рассматриваемом случае представляет собой передачу денег продавцом покупателю. Знание свойств структуры соединений в данном случае помогает лучше понять особенности рынка.

Задачи поиска сочетаний. Студенты обращаются с заявлениями на замещение должностей в таких общественных организациях, как общественные клубы, университеты или высшие медицинские учебные заведения. Элементы соответствуют студентам и институтам, тогда как связи соответствуют приложениям. Мы хотим найти методы, устанавливающие соответствие между вакантными должностями и заинтересованными в их получении студентами.

Сети. Сеть вычислительных машин состоит из взаимосвязанных узлов, которые посылают, передают дальше и получают сообщения различных видов. Мы заинтересованы не только в обеспечении возможности получать сообщения из любого другого узла, но и в том, чтобы эта возможность сохранялась для всех пар узлов и в случае изменения конфигурации сети. Например, возможно, потребуется проверить работу конкретной сети, чтобы убедиться в отсутствии некоторого небольшого подмножества узлов или соединений, настолько критичного для работы всей сети, что его утрата может привести к разъединению остальных пар узлов.

Структура программы. Компилятор строит графы для представления структуры вызовов крупной системы программного обеспечения. Элементами в этом случае являются различные функции или программные модули, составляющие систему; соединения отождествляются либо с возможностью того, что одна функция может вызвать другую функцию (статический анализ), или с фактическим вызовом, когда система находится в рабочем состоянии (динамический анализ). Нам нужно выполнить анализ графа, чтобы определить, как достичь максимальной эффективности при выделении системных ресурсов для конкретной программы.

Эти примеры демонстрируют, насколько широк диапазон приложений, для которых граф служит подходящей абстракцией, и, соответственно, диапазон вычислительных задач, с которыми доведется столкнуться при работе с графами.

Модели графов, в которых с каждым ребром связывают веса или стоимости, используются во многих приложениях. В картах авиалиний, в которых ребрами отмечены авиарейсы, такие веса означают расстояния или стоимость проезда. В электронных схемах, где ребра представляют электрические соединения, веса могут означать длину соединения, его стоимость или время, необходимое для распространения по ней сигнала. В задачах календарного планирования веса могут представлять время или расходы, затрачиваемые на выполнение задач, либо время ожидания завершения соответствующей задачи. Естественно, в таких ситуациях возникают вопросы, касающиеся различных аспектов минимизации стоимости. Наиболее изучены алгоритмы решения двух задач такого рода:

1) Определение пути с наименьшей стоимостью, соединяющего все точки;

2) Отыскание пути наименьшей стоимости, соединяющего две заданных точки.

Первый тип алгоритма применяется для решения задач на неориентированных графах, которые представляют такие объекты как электрические цепи, находит минимальное остовное дерево. Второй тип алгоритма, применяемый для решения задач на орграфах, которые представляют такие объекты, как карты авиарейсов, определяет кратчайшие пути. Эти алгоритмы находят широкое применение не только в приложениях, связанных со схемами авиарейсов и электрическими схемами, они используются также и при решении задач, возникающих во взвешенных графах.

Задача поиска минимального остовного дерева произвольного взвешенного неориентированного графа получила множество важных применений, и алгоритмы ее решения были известны, по меньшей мере, с двадцатых годов прошлого столетия. Тем не менее, эффективность ее реализации колеблется в широких пределах, а исследователи до сих пор заняты поисками более совершенных методов.

Литература

1. Кpистофидес, H. Теоpия гpафов. Алгоритмический подход. М. "Миp", 1978

2. Бондарев В.М., Рублинецкий В.И., Качко Е.Г. Основы программирования / Харьков: Фолио; Ростов на Дону: Феникс, 1997. – 368 .

3. Захарова, Л.Е. Алгоритмы дискретной математики: учебное пособие. – Моск. гос. ин-т электроники и математики. М., 2002, 120 с.

4. Кормен Т. Х., Лейзерсон Ч. И., Ривест Р. Л., Штайн К. Алгоритмы: построение и анализ, 2-е изд. — М.: Вильямс, 2005. — 1296 с.

5. Седжвик, Роберт Фундаментальные алгоритмы на C++. Алгоритмы на графах: Пер. с англ./ Роберт Седжвик. - СПб: ООО «ДиаСофтЮП», 2002. - 496 с.

6. http://www.algolist.manual.ru/links/

7. http://www.devel.vcity.ru/library.tmpl?05344_article_id=8

8. http://www.ergeal.ru/txt/archive/cs/discra/index.htm

9. Hечепуpенко, М.И. Алгоpитмы и пpогpаммы pешения задач на гpафах и сетях. – Hовосибиpск: Hаука, 1990

10. Алгоритм Флойда-Уоршелла // [Электронный ресурс]: Энциклопедия Википедия. – Электрон. дан. – Режим доступа: http://ru.wikipedia.org/wiki/Алгоритм_Флойда_—_Уоршелла. – Загл. с экрана.

11. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. – М.: Бином, 2000. – 960с.

12. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергоатомиздат, 1988.

13. Липский В. Комбинаторика для программистов: Пер. с польск. – М.: Мир, 1988. – 213 с.

14. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2004. – 368с.

15. Оре О. Теория графов. – М.: Наука, 1980.

 

Приложение

Реализация алгоритма Прима-Краскала на языке Паскаль

1. Листинг программы:

uses wincrt;

Const

N=5; {N - число вершин графа}

type

Matrix=array[1..N,1..N] of Integer; {матрица расстояний графа}

var

D,Ostov: Matrix; {D - матрица весов исходного графа, Ostov - матрица весов искомого остова}

color_of_top: array[1..N] of integer; {цвет вершин графа}

i,j,k,x,y,d_min: Integer; {d_min - текущая минимальная длина ребра}

ne_virozhd: Boolean;

BEGIN

ClrScr;

{Инициализируем граф - вводим матрицу весов графа D[i,j]}

for i:=1 to N do begin

WriteLn('Введите элементы ',i,'-й строки матрицы весов графа:');

WriteLn('Если вершины не связаны ребром - вводим любое отрицательное число');

for j:=1 to N do begin

   Write('D[',i,',',j,']='); Read(D[i,j]);

end;

end;

{Выводим матрицу весов графа D[i,j]}

WriteLn;

WriteLn('Матрица весов графа:');

for i:=1 to N do begin

for j:=1 to N do begin

   If D[i,j]>=0 then Write(D[i,j]:5) else Write(' x');

end;

WriteLn;

end;

{Инициализируем матрицу остовного дерева графа}

for i:=1 to N do

for j:=1 to N do

  Ostov[i,j]:=0;

{"Раскрашиваем" вершины графа в разные цвета}

for i:=1 to N do

color_of_top[i]:=i;

k:=0; {k - число ребер остовного дерева}

ne_virozhd:=false;

{Общий шаг алгоритма}

while k<N-1 do begin

{Задаем первоначальное значение длины искомого ребра, заведомо большее всех имеющихся у графа}

d_min:= 30000;

{Находим ребро минимальной длины, не включенное до этого в остов графа}

for i:=1 to N-1 do

for j:=i+1 to N do

   if (i<>j)and(D[i,j]>0) and (D[i,j]<d_min) and (color_of_top[i]<>color_of_top[j]) then

     begin

       d_min:=D[i,j];

       x:=i;

       y:=j;

       ne_virozhd:=true;

     end;

if ne_virozhd=true then begin

{Включаем найденное ребро минимальной длины в остов}

Ostov[x,y]:=D[x,y];

{Меняем цвет всех вершин, входящих в остов, на один цвет}

for i:=1 to N do

  if color_of_top[i] = y then color_of_top[i] := x;

end;

{Увеличиваем количество рассмотренных ребер}

k:=k+1;

end;

{Выводим матрицу весов остова}

WriteLn;

WriteLn('Искомая матрица весов остова:');

for i:=1 to N do begin

for j:=1 to N do begin

  If Ostov[i,j]>0 then Write(Ostov[i,j]:5) else Write(' x');

end;

WriteLn;

end;

END.

Блок-схема алгоритма