 |
Главная |
Понятие фибоначчиевы кучи
|
из
5.00
|
Оглавление
Введение. 3
Глава I. Фибоначчиевы кучи. 4
1.1. Двоичные кучи.. 4
1.2. Области применения.. 5
1.3. Свойства и операции на кучах.. 5
1.4. Понятие фибоначчиевы кучи.. 7
1.5. Добавление элемента.. 11
1.6. Время выполнения различных операций для трёх видов сливаемых куч (n – общее число элементов в кучах на момент операции).. 13
1.7. Оценки времени работы.. 14
Глава II. Пример реализации алгоритма Дейкстры в среде Delphi 15
2.1. Алгоритм Дейкстры.. 15
2.2. Интерфейс. 18
2.3. Кодовая реализация.. 21
Заключение. 26
Литература. 28
Приложение. 29
Приложение 1. Листинг программы «Алгоритм Дейкстры».. 29
Приложение 2. Тестовое задание.. 36
Введение
Существует много задач, где применяется работа с графами. При такой работе более целесообразно использовать фибоначиевы кучи.
При помощи фибоначиевых куч можно легко проводить сортировку, удалять, добавлять, уменьшать ключи, вершины, элементы.
Фибоначчиевы кучи ввел М.Фредман и Р.Тарьян. В их статье описаны также приложения фибоначчиевых куч к задачам о кратчайших путях из одной вершины, о кратчайших путях для всех пар вершин, о паросочетаниях с весами и о минимальном покрывающем дереве.
Теоретически фибоначчиевы кучи особенно полезны, если число операций удаления мало по сравнению с остальными операциями. Такая ситуация возникает во многих приложениях.
Объект данной курсовой- фибоначчиевы кучи.
Цель- научиться работать с фибоначчиевыми кучами.
Задачи:
1. Изучить теорию по теме фибоначиевы кучи.
2. Научиться на практике применять полученные знания.
3. Создать программу, использующую, алгоритм Дейкстры
Актуальность: алгоритм Дейкстры очень сложен для ручного расчета, поэтому его реализация очень актуальна.
Глава I. Фибоначчиевы кучи
Двоичные кучи
Для того, чтобы лучше понять, что такое фибоначчиевы кучи, следует вначале рассмотреть общее понятие кучи.
Структура "Двочная куча" (Binary Heap) позволяет хранить пары ключ-значение (key-value), и быстро выполнять операцию извлечения пары с минимальным значением ключа и операцию добавления новых пар.
С помощью двоичной кучи обычно реализуется очередь с приоритетами --- структура, позволяющая хранить объекты с приоритетами (например задания с приоритетами), извлекать самый приоритетный объект, добавлять новые объекты, быстро обновлять их приоритеты.

Рисунок 1
Области применения
Кучи являются основной структурой данных во многих приложениях. В том числе, они применяются:
· при сортировке элементов;
· в алгоритмах выбора, для поиска минимума и/или максимума, медианы;
· в алгоритмах на графах, в частности, при построении минимального остовного дерева алгоритмом Крускала (Joseph Kruskal), при нахождении кратчайшего пути алгоритмом Дейкстры (Edsger W. Dijkstra).
Свойства и операции на кучах
В общем случае куча представляет собой одно или несколько деревьев с явно выделенными корнями, элементы хранятся в вершинах. Основное свойство кучи (heap order): ключ каждой вершины не меньше, чем ключ её родителя. В дальнейшем корень дерева T будем обозначать как root(T), а значение ключа в вершине t как value(t).
Основными операциями на кучах можно считать:
· MAKE(x) - создание кучи из элемента x;
· INSERT(x, h) - добавление нового элемента x в кучу h;
· MELD(h1, h2) - слияние куч h1 и h2;
· FIND-MIN(h) - поиск минимального элемента в куче h;
· DELETE-MIN(h) - удаление минимального элемента из кучи h;
· DECREASE(x, h, y) - замена ключа x на меньший ключ y в куче h;
· DELETE(x, h) - удаление произвольного элемента x из кучи h.
Этот список нельзя назвать исчерпывающим, так как в некоторых приложениях могут потребоваться какие-то иные операции, которые в реализации могут использовать данные, а могут быть и независимыми.
Понятие фибоначчиевы кучи
Название рассматриваемых куч связано с использованием чисел Фибоначчи при анализе трудоемкости выполнения операций. В отличие от биномиальных куч, в которых операции вставки, поиска элемента с минимальным ключом, удаления, уменьшения ключа и слияния выполняются за время  , в фибоначчиевых кучах они выполняются более эффективно. Операции, не требующие удаления элементов, в этих кучах имеют учетную стоимость
, в фибоначчиевых кучах они выполняются более эффективно. Операции, не требующие удаления элементов, в этих кучах имеют учетную стоимость  . Теоретически фибоначчиевы кучи особенно полезны, если число операций удаления мало по сравнению с остальными операциями. Такая ситуация возникает во многих приложениях.
. Теоретически фибоначчиевы кучи особенно полезны, если число операций удаления мало по сравнению с остальными операциями. Такая ситуация возникает во многих приложениях.
Например, алгоритм, обрабатывающий граф, может вызывать процедуру уменьшения ключа для каждого ребра графа. Для плотных графов, имеющих много ребер, переход от  к
к  в оценке времени работы этой операции может привести к заметному уменьшению общего времени работы. Наиболее быстрые известные алгоритмы для задач построения минимального остовного дерева или поиска кратчайших путей из одной вершины используют фибоначчиевы кучи.
в оценке времени работы этой операции может привести к заметному уменьшению общего времени работы. Наиболее быстрые известные алгоритмы для задач построения минимального остовного дерева или поиска кратчайших путей из одной вершины используют фибоначчиевы кучи.
К сожалению, скрытые константы в асимптотических оценках трудоемкости велики и использование фибоначчиевых куч редко оказывается целесообразным: обычные двоичные (  -ичные) кучи на практике эффективнее. С практической точки зрения желательно придумать структуру данных с теми же асимптотическими оценками, но с меньшими константами. Такие кучи будут рассмотрены в следующих разделах.
-ичные) кучи на практике эффективнее. С практической точки зрения желательно придумать структуру данных с теми же асимптотическими оценками, но с меньшими константами. Такие кучи будут рассмотрены в следующих разделах.
При отсутствии операций уменьшения ключа и удаления элемента фибоначчиевы кучи имели бы ту же структуру, что и биномиальные. Но в общем случае фибоначчиевы деревья обладают большей гибкостью, чем биномиальные. Из них можно удалять некоторые узлы, откладывая перестройку дерева до удобного случая.
Строение фибоначчиевой кучи. Каждая фибоначчиева куча состоит из нескольких деревьев. В отличие от биномиальных деревьев, здесь дети любого узла могут записываться в любом порядке. Они связываются в двусторонний циклический список. Каждый узел  этого списка имеет поля
этого списка имеет поля  и
и  , указывающие на его соседей в списке. На рис. 1.0 показано схематическое строение фибоначчиевой кучи.
, указывающие на его соседей в списке. На рис. 1.0 показано схематическое строение фибоначчиевой кучи.
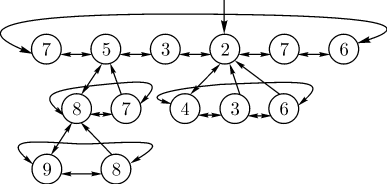
Рисунок 2
Двусторонние циклические списки удобны по двум причинам. Во-первых, из такого списка можно удалить любой узел за время  . Во-вторых, два таких списка можно соединить в один за время
. Во-вторых, два таких списка можно соединить в один за время  .
.
Помимо указанной информации, каждый узел имеет поле  , где хранится его степень (число детей), а также поле
, где хранится его степень (число детей), а также поле  . В этом поле хранится булевское значение. Смысл его таков:
. В этом поле хранится булевское значение. Смысл его таков:  истинно, если узел
истинно, если узел  потерял ребенка после того, как он в последний раз сделался чьим-либо потомком. Позже будет ясно, как и когда это поле используется.
потерял ребенка после того, как он в последний раз сделался чьим-либо потомком. Позже будет ясно, как и когда это поле используется.
Корни деревьев, составляющих фибоначчиеву кучу, также связаны с помощью указателей  и
и  в двусторонний циклический список, называемый корневым списком. Таким образом, каждый узел фибоначчиевой кучи представляется записью вида
в двусторонний циклический список, называемый корневым списком. Таким образом, каждый узел фибоначчиевой кучи представляется записью вида

Доступ к куче  производится ссылкой
производится ссылкой  на узел с минимальным ключом. Кроме того, общее число узлов задается атрибутом
на узел с минимальным ключом. Кроме того, общее число узлов задается атрибутом  .
.
Потенциал. При анализе учетной стоимости операций используют метод потенциала. Пусть  — число деревьев в корневом списке кучи
— число деревьев в корневом списке кучи  , а
, а  — количество помеченных узлов. Потенциал определяется формулой
— количество помеченных узлов. Потенциал определяется формулой

В каждый момент времени в памяти может храниться несколько куч; общий потенциал по определению равен сумме потенциалов всех этих куч. В дальнейшем мы выберем единицу измерения потенциала так, чтобы единичного изменения потенциала хватало для оплаты  операций (формально говоря, мы умножим потенциал на подходящую константу). В начальном состоянии нет ни одной кучи и потенциал равен
операций (формально говоря, мы умножим потенциал на подходящую константу). В начальном состоянии нет ни одной кучи и потенциал равен  . Как и положено, потенциал всегда неотрицателен.
. Как и положено, потенциал всегда неотрицателен.
Максимальная степень Через  обозначим верхнюю границу для степеней узлов в кучах, которые могут появиться при выполнении операций. Аргументом функции
обозначим верхнюю границу для степеней узлов в кучах, которые могут появиться при выполнении операций. Аргументом функции  является общее число всех узлов в куче, обозначаемое через
является общее число всех узлов в куче, обозначаемое через  .
.
Мы не будем углубляться в анализ трудоемкости операций с фибоначчиевыми кучами, отсылая читателя к соответствующей литературе, скажем только, что  и все операции, кроме операции удаления элемента, имеют амортизационную трудоемкость
и все операции, кроме операции удаления элемента, имеют амортизационную трудоемкость  , а операция удаления —
, а операция удаления —  .
.
Впоследствии Д.Дрисколл и Р.Тарьян разработали структуру данных, называемую  , как замену для фибоначчиевых куч. Есть две разновидности такой структуры данных. Одна из них дает те же оценки учетной стоимости, что и фибоначчиевы кучи. Другая — позволяет выполнять операцию
, как замену для фибоначчиевых куч. Есть две разновидности такой структуры данных. Одна из них дает те же оценки учетной стоимости, что и фибоначчиевы кучи. Другая — позволяет выполнять операцию  за время
за время  в худшем случае, а операции
в худшем случае, а операции  и Delete — за время
и Delete — за время  в худшем случае. Эта структура данных имеет также некоторые преимущества по сравнению с фибоначчиевыми кучами при использовании в параллельных алгоритмах.
в худшем случае. Эта структура данных имеет также некоторые преимущества по сравнению с фибоначчиевыми кучами при использовании в параллельных алгоритмах.
Фибоначчиева куча является структурой данных для хранения данных позволяющей быстро производить следующие операции: добавление элемента, получение минимального элемента, удаление минимального элемента, уменьшение ключа по ссылке и удаление по ссылке. Данная структура организована следующим образам:
1. Существует явная ссылка на минимальный элемент.
2. У каждой вершины есть ссылка на правый и левый элемент в двусвязном списке содержащим эту вершину.
3. У каждой вершины есть ссылка child указывающая на одну из вершин спика ее детей.
4. У каждой вершины есть ссылка parent указывающая на родителя.
5. У каждой вершины есть булевское поле marked использующаяся при уменьшение ключа (см. ниже). Оно истинно если вершина потеряла ребенка после того как сделалась чьим-нибудь ребенком.
6. Список содержащей минимальную вершину называется корневым списком и родители всех его вершин отсутствуют.
Рассмотрим теперь реализуемые алгоритмы по отдельности.
Добавление элемента
Добавим нашу вершину в корневой список. Если окажется, что значение её ключа меньше минимального, то она становиться новой минимальной вершиной.
Создание пустой кучи
Ссылка minElement зануляется.
|
из
5.00
|
Обсуждение в статье: Понятие фибоначчиевы кучи |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

