Удаление минимального элемента

Удаление минимального элемента состоит из двух частей. Сначала мы удаляем минимальную вершину из кучи, а всех ее детей добляем в корневой список. После этого мы объединяем вершины из корневого списка в вершины большей степени. Для этого мы создаем массив ссылок на элементы нашей кучи (индекс соответствует степени вершины). Просмотрим все вершины корневого списка занося их в массив, если окажется, что тот элемент, куда мы хотим занести нашу вершину, уже занят, то мы объединим эти две вершины в одну большей степени, сделав вершину с большим ключом ребенком вершины с меньшим ключом. Получившуюся вершину попробуем опять занести в массив и т. д. После добавим все вершины из массива в корневой спиок, находя паралельно минимум.

 

Уменьшение ключа

Данный алгоритм делится на два случая:

1. Новый ключ вершины больше ключа родителя. Тогда достаточно уменьшить ключ вершины до нового значения.

2. Новый ключ вершины меньше ключа родителя. Тогда перенесем нашу вершину в корневой список. После этого рассмотрим цепочку предков нашей вершины (её родитель, родитель ее родителя и т. д.). Найдем в этой цепочке первую неотмеченную вершину. Все вершины до нее переместим в корневой список, а ее отметим.

Удаление вершины

Для удаление вершины сначала уменьшим ее значение до «минус бесконечности», а потом удалим минимальную вершину.

Время выполнения различных операций для трёх видов сливаемых куч (n – общее число элементов в кучах на момент операции).

Процедура	Двоичные кучи (в худшем случае)	Биномиальные кучи (в худшем случае)	Фибоначчиевы кучи (учётная стоимость)
Создание	Q (1)	Q (1)	Q (1)
Вставка	Q (log n)	O(log n)	Q (1)
Найти мин.	Q (1)	O(log n)	Q (1)
Удалить мин.	Q (log n)	Q (log n)	O(log n)
Слить	Q (n)	O(log n)	Q (1)
Уменьшить ключ	Q (log n)	Q (log n)	Q (1)
Удалить	Q (log n)	Q (log n)	O(log n)

Оценки времени работы

Сводная таблица амортизированного времени работы:

 

Операция	Binary	Leftist	Top-Down Skew	Bottom-Up Skew	Pairing	Binomial	Fibonacci	2-3	Soft
MAKE	O(1)	O(1)	O(1)	O(1)	O(1)	O(1)	O(1)	O(1)	O(1)
INSERT	O(log N)	O(log N)	O(log N)	O(1)	O(log N) *	O(log N)	O(1)	O(1)	O(log 1/E)
MELD	O(N)	O(log N)	O(log N)	O(1)	O(log N) *	O(log N)	O(1)	O(log N)	O(1)
FIND-MIN	O(1)	O(1)	O(1)	O(1)	O(1)	O(log N)	O(1)	O(1)	O(1)
DELETE-MIN	O(log N)	O(log N)	O(log N)	O(log N)	O(log N)	O(log N)	O(log N)	O(log N)	O(1)
DECREASE	O(log N)	O(log N)	O(log N)	O(log N)	O(log N) *	O(log N)	O(1)	O(1)	O(1)
DELETE	O(log N)	O(log N)	O(log N)	O(log N)	O(log N)	O(log N)	O(log N)	O(log N)	O(1)

^* Для Pairing куч операции добавления элемента, уменьшения ключа и слияния гипотетически выполняются за время O(1), но данная оценка еще не доказана.

Глава II. Пример реализации алгоритма Дейкстры в среде Delphi

Алгоритм Дейкстры

Алгори́тм Де́йкстры — алгоритм на графах , изобретенный Э. Дейкстрой . Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса.

Неформальное определение.

Вариант 1. Дана сеть автомобильных дорог, соединяющих города Львовской области. Найти кратчайшие расстояния от Львова до каждого города области (если двигаться можно только по дорогам).

Вариант 2. Имеется некоторое количество авиарейсов между городами мира, для каждого известна стоимость. Найти минимальную стоимость маршрута (возможно, с пересадками) от Копенгагена до Новосибирска .

Вариант 3. Есть план города с нанесёнными на него местами расположения пожарных частей. Определить ближайшую к каждому дому пожарную станцию.

Формальное определение.

Дан простой взвешенный граф G ( V , E ) без петель и дуг отрицательного веса. Найти кратчайшее расстояние от некоторой вершины a графа G до всех остальных вершин этого графа.

 Неформальное определение.

Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины до a . Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.

Инициализация . Метка самой вершины a полагается равной 0, метки остальных вершин — бесконечности. Это отражает то, что расстояния от a до других вершин пока неизвестны. Все вершины графа помечаются как непосещенные.

Шаг алгоритма . Если все вершины посещены, алгоритм завершается. В противном случае из еще не посещенных вершин выбирается вершина u , имеющая минимальную метку. Мы рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом. Вершины, соединенные с вершиной u ребрами, назовем соседями этой вершины. Для каждого соседа рассмотрим новую длину пути, равную сумме текущей метки u и длины ребра, соединяющего u с этим соседом. Если полученная длина меньше метки соседа, заменим метку этой длиной. Рассмотрев всех соседей, пометим вершину u как посещенную и повторим шаг.

Описание

В простейшей реализации для хранения чисел d [ i ] можно использовать массив чисел, а для хранения принадлежности элемента множеству U — массив булевских переменных.

В начале алгоритма расстояние для начальной вершины полагается равным нулю, а все остальные расстояния заполняются большим положительным числом (большим максимального возможного пути в графе ). Массив флагов заполняется нулями. Затем запускается основной цикл.

На каждом шаге цикла мы ищем вершину с минимальным расстоянием и флагом равным нулю. Затем мы устанавливаем в ней флаг в 1 и проверяем все соседние с ней вершины. Если в ней расстояние больше, чем сумма расстояния до текущей вершины и длины ребра, то уменьшаем его. Цикл завершается когда флаги всех вершин становятся равны 1, либо когда у всех вершин c флагом 0 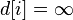. Последний случай возможен, если и только если граф G несвязан.

В разработанном приложении рассчитывается расстояние от выбранной пожарной части до всех остальных города N.

Технические задачи:

1. разработка интерфейса;

2. реализация ввода данных пользователем;

3. осуществление расчета расстояния;

4. организация вывода результата пользователю.

Интерфейс

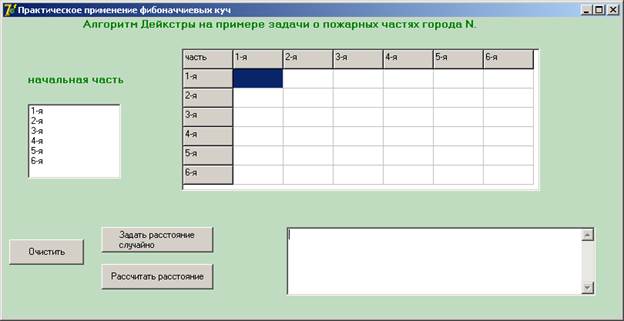
Интерфейс программы включает в себя окно ввода информации, окно выбора начальной пожарной части, три кнопки: очистка, ввод данных и расчет, а так же окно вывода результата.

 

При нажатии на кнопку «задать расстояние случайно» задается расстояние при помощи random из максимально допустимой длины MAXPATH.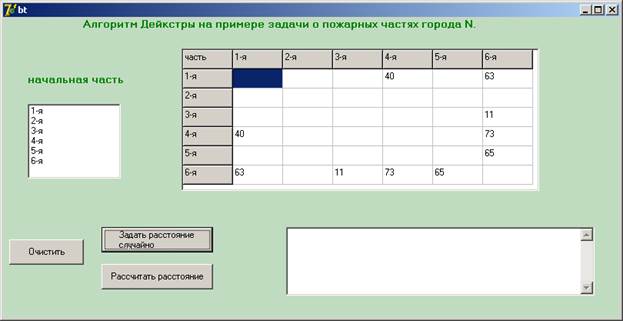

При нажатии кнопки «рассчитать расстояние» программа сначала заполняет матрицу весов, т.е. перебрасывает пути из таблицы в матрицу, потом проверяет, выбрана ли начальная часть. Если начало выбрано пользователем, то вначале находится прямой путь между частями, а после не прямой. И в конце работы программы выводится результат- все допустимые пути.    

        

 

Если начальная пожарная часть не выбрана, то об этом сообщается пользователю в виде сообщения.

 

При нажатии «очистить» происходит очистка таблицы значений и окна вывода результатов.

Кодовая реализация

    Первая процедура TForm1.Button4Click задает пути случайным образом.

    Листинг 1:

flag: real; // существует ли путь

begin

for i:=1 to StringGrid1.ColCount-1 do // определяется кол- во столбцов

begin

for j:=i+1 to StringGrid1.RowCount-1 do // определяется кол- во строк

begin

   flag := random;

   if (flag>0.5) then

     begin

       StringGrid1.Cells[i,j] := IntToStr(random(MAX));// значения из const

       StringGrid1.Cells[j,i] := StringGrid1.Cells[i,j];// заполняет таблицу

     end;

end;

end;

После этого происходит заполнение матрицы весов.

    Листинг 2:

for i:=0 to CHCount-1 do // счетчик на значения

Weights[i,i] := 0; // из части в сам себя

for i:=0 to CHCount-1 do // счетчик на значения

for j:=0 to CHCount-1 do // счетчик на значения

begin

   if (StringGrid1.Cells[i + 1, j + 1] <> '') then

     Weights[i, j] := StrToInt(StringGrid1.Cells[i + 1, j + 1]);

end; // Если индекс ячейки не относится к шапке, то происходит заполнение

Далее при нажатии кнопки «Рассчитать» происходит вызов процедуры для расчета, которая состоит из четырех различных процедур.

Листинг 3:

GetWeightsMatrix; // перебрасываем пути в матрицу

FirstCountStep; // инициализируем расчет

StraightWay; // находим прямые пути

GoCount; // запускаем расчет

Процедура TForm1.FirstCountStep проверяет выбрана ли начальная часть, и если нужно, то сообщает об ошибке.

Листинг 4:

first := -1;

for i := 0 to CHCount - 1 do // счетчик для определения начальной части

begin

if ListBox1.Selected[i] then // если часть выбрана

   first := i; // то присваивается значение начального пути

end;

if (first = -1) then // если не выбрана

begin

MessageDlg('Ошибка: вы не выбрали начальную часть в списке!',

mtError, [mbOK], 0); // то выходит сообщение об ошибке

Процедура TForm1.FormCreate задает части в интетрфейсе.

Листинг 5:

StringGrid1.Cells[0, 0] := 'часть';

for i:= 1 to CHCount do

begin

StringGrid1.Cells[0, i] := CH[i];

StringGrid1.Cells[i, 0] := CH[i];

Listbox1.Items[i-1] := CH[i];

Процедура TForm1.StraightWay находит прямой путь между частями.

Листинг 6:

for i:= 1 to CHCount do // цикл проходящий все части

begin

if Weights[first, i] <> 0 then

Memo1.lines.Add(ListBox1.Items[first] + '=>' + INtToStr(i) +

'(' + IntToStr(Weights[first, i]) + ')'); // выводится в компоненте Memo1 путь

Процедура TForm1.GoCount находит непрямой путь между частями.

Листинг 7:

n := 0; // значение пути

str := (ListBox1.Items[first] + '=>');

for j := 1 to CHCount do // счетчик

begin

for i := 0 to CHCount-1 do // счетчик

begin

   if Weights[first, i] <> 0 then // прямой путь

     if Weights[i, j] <> 0 then // непрямой путь

       begin

         n := n + Weights[first, i] + Weights[i, j]; // просчитывается путь прямой + непрямой

         str := str + ListBox1.items[i] + '=>';

       end;

end;

Memo1.Lines.Add(str + IntToStr(j) + '('+IntToStr(n)+')') // выводится результат

Процедура TForm1.Button1Click производит очистку.

Листинг 8:

for i:= 1 to CHCount do // счетчик

for j:= 1 to CHCount do // счетчик

begin

StringGrid1.Cells[j, i] := ''; // очистка

end;

Memo1.Lines.Clear; // очистка

Заключение

В первой главе данной курсовой работы было рассмотрено понятие фибоначчиевы кучи, их основные свойства и операции над ними.

       Фибоначчиева куча является структурой данных для хранения данных позволяющей быстро производить следующие операции: добавление элемента, получение минимального элемента, удаление минимального элемента, уменьшение ключа по ссылке и удаление по ссылке.

    Во второй главе был реализован алгоритм Дейкстры на примере задачи о пожарных частях.

Сложность алгоритма Дейкстры зависит от способа нахождения вершины v , а также способа хранения множества непосещенных вершин и способа обновления меток. Обозначим через n количество вершин, а через m — количество ребер в графе G .

· В простейшем случае, когда для поиска вершины с минимальным d [ v ] просматривается все множество вершин, а для хранения величин d — массив, время работы алгоритма есть O ( n ² + m ) . Основной цикл выполняется порядка n раз, в каждом из них на нахождение минимума тратится порядка n операций, плюс количество релаксаций (смен меток), которое не превосходит количества ребер в исходном графе.

· Для разреженных графов (то есть таких,для которых m много меньше n²) непосещенные вершины можно хранить в двоичной куче, а в качестве ключа использовать значения d [ i ], то время извлечения вершины из 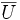станет log n , при том, что время модификации d [ i ] возрастет до log n . Т.к. цикл выполняется порядка n раз, а количество релаксаций не больше m, скорость работы такой реализации O ( n log n + m log n )

· Если для хранения непосещенных вершин использовать фибоначчиевы кучи, у которых удаление происходит за O (log n ) , а уменьшение значения за O (1) , то время работы алгоритма составит O ( n log n + m )

Нетрудно показать, что скорость работы алгоритма при использовании фибоначчиевых куч является асимптотически оптимальной и улучшить её нельзя. Так, с одной стороны, задачу сортировки массива из n элементов можно свести к задаче о поиске кратчайших путей на графе из n вершин; с другой стороны, алгоритму требуется просмотреть все ребра графа, хотя бы по одному разу.

 

Литература

1. Ананий В. ЛевитинГлава 9. Жадные методы: Алгоритм Дейкстры // Алгоритмы: введение в разработку и анализ = Introduction to The Design and Analysis of Aigorithms. — М.: «Вильямс» , 2006. — С. 189-195. — ISBN 0-201-74395-7

2. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — М.: МЦНМО, 2001.

3. Статьи «Фибоначчиевы кучи» и «Алгоритм Дейкстры» сайта www.wikipedia.org.

4. Э. Рейнгольд, Ю. Нивергельд, Н. Део. Комбинаторные алгоритмы. Теория и практика. Пер. с англ. – М., Мир, 1980.

5. Ульман Д.Д.Алгоритм Дейкстры. – «Intertera», апр. 2007.

 

Приложение

Приложение 1. Листинг программы «Алгоритм Дейкстры».

{************************************************************}

{                                                                                                                  }

{            Алгоритм Дейкстры                                                               }

{  Copyright (c) 2008 ТГИМЭУиП                                                     }

{ Факультет управления/ 461 группа                                                  }

{                                                                                                                   }

{ Разработчик: Долганова Анастасия                                                     }

{ Модифицирован: май 2008                                                                    }

{                                                                                                                   }

{************************************************************}

unit Unit1;

 

interface

 

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls, Grids, jpeg, ExtCtrls;

 

const

MAX = 200; // максимальная длина пути между двумя вершинами

CHCOUNT = 6; // количество частей

 

type

TForm1 = class(TForm)

StringGrid1: TStringGrid;

Label1: TLabel;

Memo1: TMemo;

Button4: TButton;

Button6: TButton;

ListBox1: TListBox;

Label2: TLabel;

Button1: TButton;

procedure Button4Click(Sender: TObject);

procedure Button6Click(Sender: TObject);

procedure FormCreate(Sender: TObject);

procedure Button1Click(Sender: TObject);

private

// матрица весов (расстояний между частями)

Weights: array [0..CHCOUNT-1, 0..CHCOUNT-1] of integer;

// индекс части- пункта отправления

first: integer;

procedure GetWeightsMatrix;

procedure FirstCountStep;

procedure GoCount;

procedure StraightWay;

public

{ Public declarations }

end;

 

var

Form1: TForm1;

 

implementation

 

{$R *.dfm}

 

const CH: array [1..6] of string[3]=

           ('1-я', '2-я', '3-я',

           '4-я', '5-я', '6-я');

 

procedure TForm1.Button4Click(Sender: TObject); // задает пути между частями случайным образом

var

i, j: integer;

flag: real; // существует ли путь

begin

for i:=1 to StringGrid1.ColCount-1 do

begin

for j:=i+1 to StringGrid1.RowCount-1 do

begin

   flag := random;

   if (flag>0.5) then

     begin

       StringGrid1.Cells[i,j] := IntToStr(random(MAX));

       StringGrid1.Cells[j,i] := StringGrid1.Cells[i,j];// заполняет таблицу

     end;

end;

end;

end;

 

 

procedure TForm1.GetWeightsMatrix; // заполняет матрицу весов Weights

var

i, j: integer;

begin

for i:=0 to CHCount-1 do

Weights[i,i] := 0; // из части в саму себя

for i:=0 to CHCount-1 do

for j:=0 to CHCount-1 do

begin

   if (StringGrid1.Cells[i + 1, j + 1] <> '') then

     Weights[i, j] := StrToInt(StringGrid1.Cells[i + 1, j + 1]);

end;

end;

 

procedure TForm1.Button6Click(Sender: TObject); вызывает процедуры для расчета

begin

Memo1.Lines.Clear;

GetWeightsMatrix; // перебрасывает пути в матрицу

FirstCountStep; // инициализирует расчет

StraightWay; // находит прямые пути

GoCount; // запускает расчет

end;

 

procedure TForm1.FirstCountStep; // проверяет, выбрана ли часть из списка

var

i: integer;

begin

first := -1;

for i := 0 to CHCount - 1 do

begin

if ListBox1.Selected[i] then

   first := i;

end;

if (first = -1) then

begin

MessageDlg(‘ ошибка: вы не выбрали начальную часть в списке!',

mtError, [mbOK], 0);

exit;

end;

end;

 

procedure TForm1.FormCreate(Sender: TObject); // задает части в интерфейсе

var

i: integer;

begin

StringGrid1.Cells[0, 0] := 'часть';

for i:= 1 to CHCount do

begin

StringGrid1.Cells[0, i] := CH[i];

StringGrid1.Cells[i, 0] := CH[i];

Listbox1.Items[i-1] := CH[i];

end;

end;

 

procedure TForm1.StraightWay; // находит прямой путь

var

i : integer;

begin

for i:= 1 to CHCount do

begin

if Weights[first, i] <> 0 then

Memo1.lines.Add(ListBox1.Items[first] + '=>' + INtToStr(i) +

'(' + IntToStr(Weights[first, i]) + ')');

end;

end;

 

procedure TForm1.GoCount; // находит непрямой путь между частями и вычисляет расстояние

var

i, n, j : integer;

str : string;

begin

n := 0;

str := (ListBox1.Items[first] + '=>');

for j := 1 to CHCount do

begin

for i := 0 to CHCount-1 do

begin

   if Weights[first, i] <> 0 then

     if Weights[i, j] <> 0 then

       begin

         n := n + Weights[first, i] + Weights[i, j];

         str := str + ListBox1.items[i] + '=>';

       end;

end;

Memo1.Lines.Add(str + IntToStr(j) + '('+IntToStr(n)+')')

end;

end;

 

procedure TForm1.Button1Click(Sender: TObject); // очистка

var

i, j: integer;

begin

for i:= 1 to CHCount do

for j:= 1 to CHCount do

begin

StringGrid1.Cells[j, i] := '';

end;

Memo1.Lines.Clear;

end;

end.