Как быть с другими схемами?

Контроль энтропии в алгоритмах

И расчетах газодинамических течений

 

Москва, 2006 год

 

УДК 519.6

Контроль энтропии в алгоритмах и расчетах газодинамических течений

Прокопов Г.П.

Препринт Института прикладной математики им. М.В.Келдыша РАН

 

    На примере одной недавно опубликованной схемы проведено аналитическое исследование поведения энтропии при численном интегрировании уравнений газовой динамики. Оно подтвердило опасение о возможности реализации в ходе расчета разрывов, которые аналогичны ударным волнам разрежения. Следовательно, может происходить нарушение постулата о неубывании энтропии. Предлагаются простые алгоритмы контроля энтропии при расчетах газодинамических течений и по другим известным численным методам.

    Работа выполнена при поддержке Российского Фонда Фундаментальных Исследований (грант № 05-01-00097).

 

 

Control of entropy in algorithms and calculations of gas-dynamics flows.

Prokopov G.P.

Preprint of Keldysh Institute of applied mathematics, RAS

 

Based on one recently published approach, an analytical investigation of entropy behaviour in process of numerical integration of gas-dynamics equations is implemented. It confirms an existence of discontinuous solutions that similar to rarefaction shock-wave in numerical calculations. So, the postulate of non-increasing entropy is disturbed. Some simple methods to control of entropy in gas-dynamic flows and other known numerical methods are suggested.

This work is support by RFFI (grant N 05-01 -00097)

 

 

Содержание

                                                                                                           стр.

 

Введение …………………………………………………………..   3

§ 1. Схема С для расчета газодинамических течений ………….   4

§ 2. Энтропийное исследование схемы С ….. …………………..   7

§ 3. О схеме С и ударной волне разрежения…………………….   10

§ 4. Нужен ли энтропийный контроль схемам типа Годунова? .   12

§ 5. Как быть с другими схемами?…………………….…………   13

§ 6. Снова о схеме C и ее экономичности ...…………………….  15

§ 7. Предложение по улучшению схемы С ………….………….   19

§ 8. О проблеме сложных уравнений состояния ………………..  23

Заключение ……………………………………………………….  26                                                                                                 

Литература ………………………………………………………...  28                                                                                          

 

Введение

    Настоящая работа является непосредственным продолжением краткой публикации автора [1]. Одной из ее целей было напоминание о том важном обстоятельстве, что в широко известном методе Годунова (см., напр., монографию [2]) успех достигается благодаря использованию дополнительного закона сохранения энтропии на гладких решениях и постулату о ее неубывании на разрывах. В связи с тем, что имеется много публикаций различных авторов, заявляющих о методах «типа Годунова», интересен вопрос, с должным ли вниманием они относятся к упомянутому обстоятельству. Естественно, что это касается и не только таких методов, но и вообще алгоритмов для расчета газодинамических течений.

    Проясняя для себя этот вопрос, автор обратился к изучению численных методов с такой точки зрения. Весьма полезной оказалась монография [3], в которой можно найти как содержательную информацию о работах многих авторов, так и ссылки, по которым можно разыскивать их публикации.

    В первую очередь автора интересовали методы расчета газодинамических течений (как нестационарных, так и стационарных), обеспечивающие выполнение законов сохранения массы, импульса и энергии, а потому основанные на использовании дивергентной формы уравнений газовой динамики. При ознакомлении с таким кругом работ удалось обнаружить слишком мало информации, касающейся поведения энтропии. Исключение составляет разве что раздел 2.10 в монографии [3], что и будет отмечено в §5.

    Попытавшись выполнить такие исследования аналитически, автор потерпел полную неудачу из-за весьма сложного характера известных и широко используемых алгоритмов.

    И вдруг в этом «темном царстве» блеснул луч надежды. На семинаре им.К.И.Бабенко в ИПМ им.М.В.Келдыша 26 октября 2006 г. был сделан доклад по результатам работы [4]. Эта очень небольшая по объему публикация производит впечатление на специалиста, знающего в деталях содержание вопроса, чрезвычайной простотой предлагаемого алгоритма для приближенного решения задачи Римана о распаде произвольного разрыва. А она является главным элементом при реализации численного метода С.К.Годунова, а также его усовершенствований и модификаций, предлагаемых различными авторами.

    Правда, следует отметить, что представленный в [4] разностный метод для уравнений газодинамики, для краткости именуемый далее схемой С (название взято из [4]), сразу же вызвал определенные сомнения. Именно в силу упомянутой его простоты по сравнению с другими методиками удалось провести аналитические исследования по интересующему вопросу о поведении энтропии, которые, к сожалению, подтвердили справедливость возникших опасений. Они будут представлены в настоящей работе.

    Эти результаты позволяют автору выступить с предложением об «энтропийном контроле», которым следует сопровождать расчеты газодинамических течений, выполняемых по методам «типа Годунова», схеме С и другим аналогичным методам.

    В § 5 автор рассматривает возможность использовать «энтропийный контроль» и при расчетах по другим методикам. Например, по представленным в монографии [3] сеточно-характеристическим схемам типа КИР (Куранта-Изаксона-Рисса), Роу, TVD-схемам и т.п.

    Основная часть работы для простоты изложена для идеального газа. Однако идея энтропийного контроля тем более необходима и может быть реализована и для сложных уравнений состояния. Но есть и проблемы, связанные с их заданием. Этим вопросам посвящен § 8.

        

§ 1. Схема С для расчета газодинамических течений.

 

    В настоящем параграфе будет практически полностью представлено описание разностной схемы из работы [4]. Сделать это целесообразно, во-первых, потому, что все приводимые формулы потребуются для дальнейшего изложения. Во-вторых, сочтено необходимым изменить некоторые обозначения, с тем, чтобы обеспечить единообразие с монографией [2], известной широкому кругу читателей, и которая тоже будет использоваться в дальнейшем изложении. Наконец, в-третьих, к счастью, нужное нам описание сделано в [4] с удивительной краткостью, занимая всего одну печатную страницу.

    Описание схемы С рассматривается на примере хорошо известных нестационарных уравнений одномерной газовой динамики в дивергентной форме:

(1.1)                    ,

где U , F – векторы для законов сохранения массы, импульса и энергии:

(1.2)           ,           

Здесь r - плотность газа, u – скорость, р – давление,

(1.3)   - полная внутренняя энергия, e - внутренняя энергия единицы массы, определяемая уравнением состояния газа.

Пока, до § 8, ограничимся простейшим уравнением состояния идеального газа с показателем адиабаты g:

(1.4)              .

Разностная схема для (1.1) записывается в виде:

(1.5)             

Здесь, как было принято в монографии [2],  - номер ячейки сетки по оси х, ограниченной узлами с номерами j -1 и j. Формула (1.5) описывает «пересчет» величин на одном шаге по времени – переход от величин с «нижнего» слоя по времени t к «верхнему».

    В методе С.К.Годунова потоки на границах ячеек F _j вычисляются посредством численного решения задач Римана о распаде разрыва с параметрами газа в соседних ячейках сетки. Этот расчет делается либо приближенно (например, в виде «звукового» приближения), либо (если необходимо) итерационным методом до достижения результата с предписываемой точностью.

    Основная идея предложенной в [4] схемы С также состоит в вычислении потоков на границах ячейки. Задача Римана решается приближенно на основе соотношений на разрывах, аналогичных описанным в [2] на стр.103:

(1.6)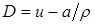                     

                        

Здесь D – скорость распространения разрыва, а – массовая скорость (вместо обозначений w,m соответственно в [4]).

Квадратными скобками [ ] обозначается разность значений величин, заключенных в скобки, по обе стороны от разрыва.

    В отличие от метода Годунова, при приближенном решении задачи Римана рассматривается упрощенная схема течения с распадом на левую волну, контактный разрыв и правую волну. Она изображена на рис.1.

    Обозначим индексами: 1 – параметры в левой ячейке сетки, 2 – в правой, 3 – между левой волной и контактным разрывом, 4 – между контакт-ным разрывом и правой волной, как показано на схеме течения (см. рис.1).

 

 

Рис. 1.

 

 

 

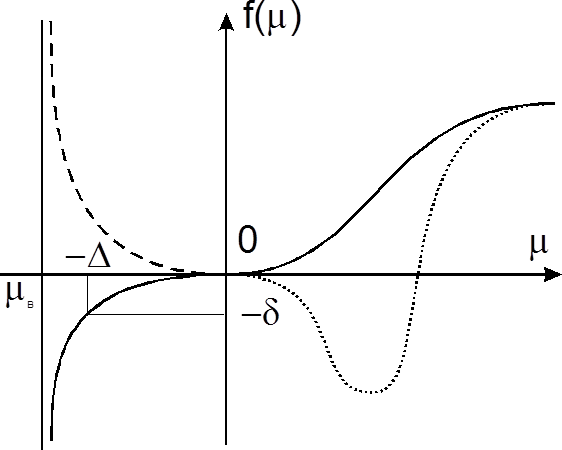
Рис. 2.

 

    Расчетные формулы имеют вид:

            ,          

            ,

(1.7)               

                     

                                       

    Назначение параметров газа ( R , U , P , E ) _j на границах ячейки для вычисления векторов потока F _j (в методе Годунова они назывались «большими» величинами) определяется значениями U , D ₁ , D ₂.

    В случае U ³0: при D ₁ ³0 эти параметры равны параметрам в зоне 1, а при D ₁ <0 – параметрам в зоне 3.

    В случае U <0: при D ₂ £0 – параметры равны их значениям в зоне 2, а при D ₂ >0 – параметрам в зоне 4.

    Определяющую роль играет назначение массовых скоростей а₁, а₂ . Для этой цели предлагается использовать формулы:

(1.8)    

           

Присутствующие в них величины с₁,с₂ представляют скорости звука, определяемые уравнением состояния. Для идеального газа (1.4) они вычисляются по формулам:

(1.9)            ,  

    По утверждению [4], такое назначение массовых скоростей а₁, а₂ обеспечивает отсутствие осцилляций на разрывах при произвольных физических параметрах в соседних ячейках разностной сетки.

    Пока ограничимся этим описанием схемы С и перейдем к ее исследованию.

 

§ 2. Энтропийное исследование схемы С.

 

    Итак, одним из принципиальных элементов конструирования схемы С является замена волны разрежения на фронт разрыва.

    Напомним, что, как отмечалось в [1], в монографии [2] на стр.115-116 была рассмотрена в качестве примера задача о распаде разрыва с симметричными данными относительно границы раздела. Если в ней заменить возникающую волну разрежения фронтом разрыва, на котором будут выполняться соотношения (1.6), то при этом реализуется так называемая ударная волна разрежения. А ее следует запрещать как нарушающую постулат о неубывании энтропии.

    В схеме С сначала «волевым» образом по формулам (1.8) назначаются массовые скорости а₁, а₂, а затем, исходя из тех же соотношений на разрыве, производится вычисление параметров, характеризующих состояние газа на разрыве. Поскольку на этом процесс их назначения заканчивается, говорить о реализации ударного фронта разрежения нет оснований. Но в каком случае можно полученный результат считать разумным и допустимым?

    Предлагается постулировать следующее положение: газ с вычисленными параметрами, определяющими величины потоков через разрыв, должен иметь энтропию, не меньшую, чем второй (исходный, «напарник») газ, участвующий в вычислении потоков.

    Представляется, что только такое требование позволит контролировать неоправданное и скрытое занижение энтропии в газодинамических расчетах. Назовем его «жестким контролем энтропии».

    Более просто было бы, например, ограничиться вычислением и контролем энтропии в ячейках сетки на верхнем слое по времени. Однако тогда, в соответствии с формулой (1.5), появляется возможность компенсировать «потери энтропии» в одном узле сетки за счет другого. Поэтому назовем его «мягким контролем энтропии». Нарушение его создает возможность конструирования, по крайней мере, «патологических» примеров недопустимых течений. Но отсюда недалеко и до возможности реализации таких ситуаций и в практических расчетах.

    Если согласиться с провозглашенным постулатом, то следующим шагом исследования должен быть вопрос: обеспечивает ли назначение массовых скоростей (1.8) его выполнение для рассматриваемой схемы С?

    Это исследование будем проводить на уже упомянутом упрощенном примере распада разрыва с симметричными данными. Итак, пусть:

(2.1)  ,    ,    ,   .

Поскольку два газодинамических параметра можно задавать независимо, можно было бы упростить формулы, полагая  , 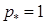. Мы сознательно не будем этого делать, чтобы не потерять возможности контролировать их с точки зрения размерности. Тогда в задаче остается один свободный параметр u _* (если не считать показателя адиабаты g в уравнении состояния (1.4), которым мы пока ограничиваемся). Отметим, что в качестве аналитического решения этой газодинамической задачи при u _*>0 (встречные потоки) реализуются ударные волны, а при u _*<0 (разбегающиеся потоки) – волны разрежения. Они распространяются симметрично от границы раздела.

    Благодаря симметрии (2.1) расчетные формулы (1.7)-(1.9) принимают более простой вид:

(2.2)      ,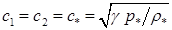    

           

           

(2.3)    

(2.4)                

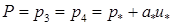
(2.5)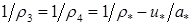          

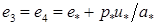
    В соответствии с назначением, описанным вслед за формулами (1.7), для «больших» величин в узле, которые обозначим R , E, получаем:

(2.6)            

    Вот теперь приступаем к исследованию энтропии. Обычно для этого привлекается энтропийная функция 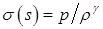. Практически будет удобнее работать с величиной .

    Заметим, что именно эта величина, с точностью до множителя с _v (удельная теплоемкость при постоянном удельном объеме), принималась за «настоящую» энтропию (см. [5], стр.33). Она остается постоянной вдоль адиабаты Пуассона. Поэтому, чтобы не вводить новых обозначений, полагаем, что

(2.7)      ,    

Условие ее неубывания принимает вид:

(2.8)   

Следовательно, из формул (2.4),(2.6) и (2.2) получаем:

(2.9)         

                      

Введя безразмерный параметр  и с учетом (2.3) получаем:

(2.10)     

Проанализируем полученную формулу сначала для случая m <0.

Тогда  и формула (2.10) приобретает вид:

(2.11)      .

Ее производная определяется формулой:

(2.12)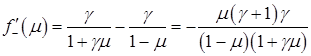   

В точке m=0 имеем 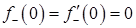. Производная  на интервале . Для значений  функция не определена.

 имеет вертикальную асимптоту при .

    Стоит заметить, что в появлении  «виновата», конечно, формула для давления (2.4): при  получалось бы Р<0.

    Теперь обратимся к случаю m>0.

Поскольку тогда , формула (2.10) приобретает вид:

(2.13)          .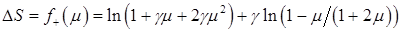

Ее производная определяется формулой:

(2.14)   

После несложных преобразований эта формула приводится к виду:

(2.15)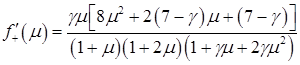   

Функция  определена для всех . .

    Квадратный трехчлен в числителе (2.15) положителен для g <7.

    Поэтому  для всех m>0, если g <7.

    В случае g>7 квадратный трехчлен достигает минимума при 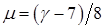 и этот минимум равен , т.е. отрицателен. Следовательно, при g>7 есть некоторый интервал, на котором . Поскольку , получается, что и  на некотором интервале , образуя «провал» ниже оси m.

   Эскиз графика функции  - сплошная кривая на рис.2 для g <7.

 При m=0 он касается оси m и при  имеет асимптотику .

    Главным (и тревожным) фактом является поведение функции f ( m ) при m <0. Она отрицательна на интервале 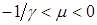, а при  вообще не определена. Это означает, что в случае разбегающихся потоков  в расчете распада разрыва получатся параметры потока, имеющего меньшую энтропию , т.е. будет нарушен сформули-рованный постулат. Налицо нарушение жесткого контроля энтропии. Поскольку опасный участок примыкает к m=0, такая ситуация реализуется при сколь угодно малых различиях параметров с индексами 1 и 2.

    В случае g>7 аналогичная ситуация наблюдается и для встречных потоков, если m попадает внутрь «провала» (см. рис.2).    

 

§ 3. О схеме С и ударной волне разрежения

 

    Полученному результату не приходится удивляться. Обратимся к уже упомянутому в начале § 2 примеру на стр.115-116 монографии [2]. В нем возникала ударная волна разрежения. Получим для нее соответствующую функцию f ( m ), аналогичную (2.10).

    Ограничимся только ее частью, отвечающей m <0. Если вместо m временно принять за параметр величину , то, с учетом описания в [2] на стр.116 и определения энтропии (2.8), можно сразу выписать формулу:

(3.1)      

Для ее производной

             

после несколько кропотливого упражнения получается красивый результат, приведенный на стр.116 в [2]:

(3.2)     

Нам не хватает только формулы, связывающей m и q. Вся информация для этого содержится в формулах (2.2)-(2.5):

(3.3)            

В результате получаем:

(3.4)   

Поскольку  , для ее производной будем иметь:

 

(3.5)        .

Отсюда следуют те выводы, которые уже приведены в [2] на стр.116-117.

    При малых значениях m получаем, что

(3.6) , , где . Следовательно, в ударной волне слабой интенсивности скачок энтропии является малой величиной третьего порядка малости по сравнению со скачком давления. Для  функция f ( m ) не определена. Поведение f ( m ) на интервале  аналогично изображенному на рис.2. То тревожное обстоятельство, что f ( m )<0 для , означает нарушение там упомянутого выше постулата, т.е. реализацию ударной волны разрежения, если скорость разбегания газов  попадает на этот участок.

    В какой-то степени утешительным можно считать тот факт, что (в силу касания третьего порядка) величина 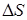 остается выше некоторого условного порога - d для значений m на протяженном отрезке. Длина его оценивается, исходя из формулы (3.6), как .

Аналогичная оценка для примера, рассмотренного в § 2, с использованием формулы (2.12) получается несколько хуже. Поскольку при малых m имеем оценку: , протяженность аналогичного отрезка

(3.7)               .

    Полученные результаты свидетельствуют о том, что при m<0 схема С реализует разрыв, на котором уменьшается энтропия, т.е. по существу похожий на ударную волну разрежения.

 

    § 4. Нужен ли энтропийный контроль схемам типа Годунова?

 

    Обратимся теперь к вопросу о том, как срабатывает энтропийный контроль для схемы Годунова. И сразу обнаруживаем, что в ней нет обсуждаемой проблемы, потому что «честно» отслеживаются границы области, занимаемой волной разрежения, в которой обеспечивается закон сохранения энтропии. Причем это обеспечивается не только в окончательном решении, но и в ходе всего итерационного процесса. Оборвать его можно в любой момент, который выберет исполнитель. Достигается это следующим образом. Как описано в монографии [2] на стр.114-115, получается очередное значение для давления . Далее в случае, если в конфигурации распада разрыва присутствует волна разрежения, значения плотности R и остальных величин, описывающих эту волну, досчитываются, исходя из адиабаты Пуассона, что тождественно сохранению значения энтропии.

    Даже при расчете исходного «звукового» приближения, получив начальное приближение для давления  по формуле (13.26) на стр.113 в [2], не стоит «соблазняться» расчетом и других величин по аналогичным линеаризованным формулам, а следует воспользоваться только что упомянутым алгоритмом с учетом адиабаты Пуассона. «Копеечная» экономия от замены их ударной адиабатой Гюгонио (или линеаризованными формулами) может обернуться ударной волной разрежения, интенсивность которой и соответствующее уменьшение энтропии еще нужно оценивать. Да и нужно ли? А описанный «честный» досчет величин даже для грубого «звукового» приближения гарантирует неубывание энтропии.

Изложенное, конечно же, не означает, что у метода Годунова вообще нет проблем. Ввиду первого порядка схемы к ним относятся прежде всего проблемы относительно низкого уровня точности, что особенно существенно при расчете гладких течений. Именно поэтому усилия многих авторов направлены на повышение порядка аппроксимации и другие его усовершенствования для повышения точности расчетов.

    Одно из направлений деятельности такого рода связано с заменой кусочно-постоянной аппроксимации текущего распределения газодинамичес-ких параметров, используемой в исходном варианте метода Годунова. Идея – подать задаче о распаде разрыва более совершенные данные, благодаря которым ожидается повышение точности.

    Работу такого рода алгоритмов можно условно разделить на этапы, выделив в отдельный подготовку таких данных, а в следующий этап – расчет распада разрыва.

    Обсуждаемый в этой работе «жесткий энтропийный контроль» предлагается применить к подготовленным входным данным для расчета распада разрыва. Цель его – убедиться, что не «нахимичили» и с энтропией все в порядке. А уж алгоритм расчета распада разрыва не подведет, если применять так, как было описано выше.

    Сказанным автор ни в какой мере не пытается принизить роль этапа подготовки совершенных данных. Напротив, по-видимому, именно это – наиболее перспективный путь развития алгоритмов такого типа.

    Теперь самое подходящее время отметить, что в качестве заключительного этапа выполняется «пересчет» значений величин в ячейке сетки с учетом потоков через ее границы. Интуитивно ясно, что это эквивалентно «смешиванию» нескольких газов, каждый из которых имеет свою энтропию. Если все новые компоненты имеют энтропию, не меньшую, чем исходный газ, неубывание энтропии для результата «смешивания» гарантировано. Во всяком случае, ограничение шага по времени по условию Куранта направлено именно на это.

    Сказанное означает, что «мягкий контроль энтропии» в ячейках сетки становится тогда излишним. Такой контроль однако не теряет своей актуальности, если «подмешиваются» компоненты с низкой энтропией.

    Очевидна и недостаточность только «мягкого» контроля. Результат контроля может быть благоприятным, хотя «кое-где у нас порой» происходило убывание энтропии, но это удалось скрыть за счет соседних узлов сетки.

 

Как быть с другими схемами?

 

    Есть еще широкий круг алгоритмов расчета газодинамических течений, реализующих законы сохранения в форме (1.5). При этом величины потоков F_j вычисляются, исходя совсем из других соображений, чем в рассмотренных выше методах «типа Годунова».

    Сюда, в частности, можно отнести многие схемы, рассмотренные в главах 2-3 монографии [3]. Не будем повторять и расширять их перечисление, сделанное во введении.

    В разделе 2.10, который называется «Энтропийная коррекция» и занимает всего лишь стр.139-144, специально рассматриваются «алгоритмы, которые позволяют избежать появления в численных результатах нефизических решений, в частности, газодинамических ударных волн разрежения. Такая коррекция вводит дополнительный механизм отбора физически приемлемого решения» (см. [3], стр.139).

    Ввиду того, что аналитическое исследование поведения энтропии слишком затруднительно из-за сложности алгоритмов, автор предлагает пойти по следующему пути.

    Будем рассматривать любой применяемый алгоритм расчета газодинамических течений посредством уравнений (1.1) как «черный ящик». Пусть (безразлично каким способом) в некотором узле сетки получены значения потоков, т.е. вектор F из трех величин (F ₁ , F ₂ , F ₃) компонент (1.2).

    Будем рассматривать его как результат для некоторого условного, гипотетического газа. Параметры этого газа должны восстанавливаться, исходя из уравнений для потоков, дополненных нужным уравнением состояния, в рассматриваемом пока случае – уравнением (1.4):

(5.1)           

(5.2)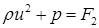           

(5.3)          

                  

    Имеем систему четырех уравнений для четырех величин . Существует ли ее единственное решение и можно ли его восстановить?

    Предположим, что решение существует.

Тогда из (5.1)-(5.3) последовательно получаем:

(5.4)        ,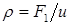     

(5.5)     

Запишем уравнение состояния в виде:

(5.6)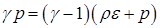     

Подставляя в него результаты (5.4)-(5.5), получаем:

(5.7)     

Это квадратное уравнение для u приводится к виду (конечно, ):

(5.8)     

Его дискриминант

(5.9)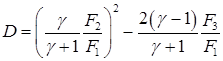     

должен быть неотрицательным. Поскольку предполагается, что решение существует, воспользуемся соотношениями (5.1)-(5.3) и подставим их в формулу (5.9):

(5.10)     

                  

                    ,

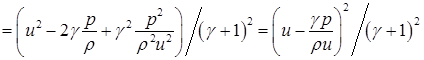что и требовалось.

    Следовательно, уравнение (5.8) может быть решено. Остается правильно распорядиться его двумя вещественными корнями:

(5.11)           ,  

Опять же, поскольку решение существует, воспользуемся соотношениями (5.1)-(5.3) и подставим их в формулы (5.11). Получим:

                   

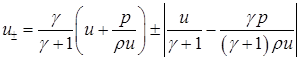
Одно из этих равенств превращается в тождество:

(5.12)           ,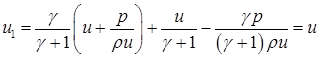

                  

При работе с формулами (5.11) определить, какой из корней является содержательным, проще всего, если вычислить оба корня и проверить их.    По значениям  и (или)  могут быть вычислены

(5.13)             ,      .

Возможность восстановить параметры условного газа по полученным значениям потоков реализуется по (5.9),(5.11) и (5.13) при условии .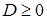

    Конечно, после этого прежде всего проверяется «разумность» полученного результата:

(5.14)         ,      .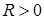

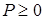Если эти условия выполнены, вступает в силу постулат об энтропии. По формуле (2.8) с привлечением параметров  газа-«напарника», участвующего в расчете потоков, вычисляется величина изменения энтропии . Результат такого «жесткого энтропийного контроля» признается правомочным только в случае, если энтропия неубывает: . Конечно (хотя бы с учетом ошибок округления), его стоит несколько ослабить:

(5.15) 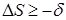          ,      или    , где  .

    Хочется пойти и на большее ослабление: в связи с обсуждением в конце § 3 и рис.2 допустимое значение  увеличить. Однако уместно заметить, что «ложка дегтя может испортить бочку меда».

    Наконец, главное: из двух корней (5.11) «хороший» должен быть и только один – иначе «грозит» неединственность или нефизичность решения основной задачи. Заметим также, что речь идет о контроле, который (пока) не влияет на расчет.

  

§ 6. Снова о схеме C и ее экономичности

 

    Вернемся снова к тревожным результатам «жесткого энтропийного контроля», полученным для схемы С уже на простейшей модельной задаче с симметричным распадом разрыва. Чем же можно тогда объяснить предъявление успешных результатов расчетов по схеме С? В частности, цитируем [4]: «Численное решение различных одномерных и пространственных задач показало, что в разработанной схеме нет проблем прохождения звуковой точки и не требуется снижение числа Куранта на сильных разрывах… Предложенный подход имеет фундаментальный характер и обобщен на стационарный случай. Разработаны монотонные схемы 2-го порядка… В качестве иллюстрации представлены результаты расчетов пяти вариантов типовых задач Торо [6]».

    Что можно выдвинуть в качестве возможных версий такого благополучного развития событий? Начнем с того, что, по-видимому, энтропией просто не интересовались.

    Оценки, сделанные в конце §3 для интервала значений m, гарантирующих попадание в условный пороговый интервал d, показывают, что, как правило, это попадание наверняка происходило.

    В таком случае возможность компенсировать «потери энтропии» в одном узле сетки за счет другого вполне реальна. Возможно, если ввести «мягкий энтропийный контроль» тол