ДЕЙСТВИЯ С КОМПЛЕКСНЫМИ ЧИСЛАМИ

     Я рассмотрел решение квадратного уравнения х² + 1 = 0. Отсюда х² = –1. Число х, квадрат которого равен –1, называется мнимой единицей и обозначается i. Таким образом, i² = -1, откуда i = . Решение квадратного уравнения, например, х² – 8х + 25 = 0, можно записать следующим образом: х =

= 4  = 4  = 4 ± = 4 3  = 4 ± 3i.

     Числа вида 4 + 3i и 4 – 3i называют комплексными числами. В общем виде комплексное число записывается a + bi, где a и b – действительные числа, а i – мнимая единица. Число a называется действительной частью комплексного числа (Re, от фр. réele – «реальный», «действительный»), bi – мнимой частью этого числа (Im, от фр. imaginaire – «мнимый»), b – коэффициентом мнимой части комплексного числа.

       Комплексные числа равны, если равны их действительные части и коэффициенты мнимых частей: a + bi = c + di, если a = c, b = d. Комплексное число равно нулю тогда, когда его действительная часть и коэффициент мнимой части равны нулю, т.е. z = a + bi = 0, если a = 0, b = 0. Действительные числа являются частным случаем комплексных чисел. Если b = 0, то a + bi = a – действительное число. Если a = 0, b ≠ 0, то a + bi = bi – чисто мнимое число. Также на множестве комплексных чисел теряются понятия "больше" и "меньше", можно лишь по отдельности сравнивать действительные и мнимые части комплексных чисел.

Комплексно-сопряжённые числа.  Сопряжёнными числами называют числа, действительные части которых равны, а мнимые отличаются знаком. Сопряжённое комплексному числу z обозначают z.

Произведением и суммой сопряжённых чисел являются действительные числа:

(a + bi) + (a – bi) = 2a,

(a + bi) ∙ (a – bi) = a² + b².

Позже, когда была предложена геометрическая интерпретация комплексных чисел, возникла необходимость введения нового понятия – длины вектора, соответствующего комплексному числу. Его стали называть модулем комплексного числа и обозначать:

по предложению швейцарского математика Жана Аргана.

Самостоятельно изучив пример , я пришёл к выводу, что и сумма корней двух сопряжённых чисел равна действительному числу. Действительно, обозначив конечный результат за x и учитывая, что обе части неотрицательны, я имею право возвести выражение в квадрат:

Раскрыв скобки и выполнив возможные действия в левой части, я получил:

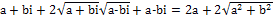. Т.е.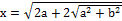

Так как a и b – действительные числа, то и это выражение будет действительным. Я доказал это на примере:

. Возведя в квадрат, я получил:

.

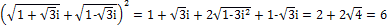Т.е. = .

Сложение комплексных чисел. Суммой двух комплексных чисел       z₁ = a + bi и z₂ = c + di называется комплексное число z = (a + c) + (b + d)i. Для комплексных чисел справедливы переместительный и сочетательный законы сложения. Их справедливость следует из того, что сложение комплексных чисел по существу сводится к сложению действительных частей и коэффициентов мнимых частей, а они являются действительными числами, для которых справедливы указанные законы.

Вычитание комплексных чисел определяется как действие, обратное сложению: разностью двух комплексных чисел a + bi и c + di называется комплексное число х + yi, которое в сумме с вычитаемым дает уменьшаемое. Отсюда, исходя из определения сложения и равенства комплексных чисел, получим два уравнения, из которых найдем, что х = a – c, у = b – d. Значит,

(a + bi) – (c + di) = (a – c) + (b – d)i.

Произведение комплексных чисел  z₁ = a + bi и z₂ = c + di называется комплексное число z = (ac – bd) + (ad + bc)i, z₁z₂ = (a + bi) ∙ (c + di) = (ac – bd) + + (ad + bc) i. Легко проверить, что умножение комплексных чисел можно выполнять как умножение многочленов с заменой i² на –1. Для умножения комплексных чисел также справедливы переместительный и сочетательный законы, а также распределительный закон умножения по отношению к сложению.

Деление комплексных чисел, кроме деления на нуль, определяется как действие, обратное умножению. Конкретное правило деления получим, записав частное в виде дроби и умножив числитель и знаменатель этой дроби на число, сопряженное со знаменателем:

Или короче: .

Степень числа i является периодической функцией с периодом 4. Я доказал это утверждение: i³ = i² ∙ i = (– 1) i = – i; i⁴ = i³ ∙ i = (– i) i = – i² = – (– 1) = 1; i⁵ =

= i⁴ ∙ i = 1 ∙ i = i; i⁶ = i⁵ ∙ i = i ∙ i = – 1. Вообще, i^{4n + k} = (i⁴)ⁿ ∙ i^k = 1ⁿ ∙ i^k.

4