Выбор шага интегрирования

Для выбора шага интегрирования можно воспользоваться выражением остаточного члена. Возьмем, например, остаточный член формулы Симпсона:

.

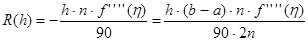Если ê  ê , то ê  ê .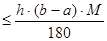

По заданной точности e метода интегрирования из последнего неравенства определяем подходящий шаг.

, .

Однако такой способ требует оценки 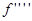 (что на практике не всегда возможно). Поэтому пользуются другими приемами определения оценки точности, которые по ходу вычислений позволяют выбрать нужный шаг h.

Разберем один из таких приемов. Пусть

,

где 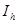 - приближенное значение интеграла с шагом . Уменьшим шаг 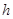 в два раза, разбив отрезок  на две равные части  и  ( ).

Тогда ,

Предположим теперь, что 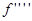 меняется не слишком быстро, так что 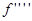почти постоянна: . Тогда  и , откуда , то есть .

Отсюда можно сделать такой вывод: если , то есть если , , а  - требуемая точность, то шаг   подходит для вычисления интеграла с достаточной точностью. Если же , то расчет повторяют с шагом  и затем сравнивают  и  и т.д. Это правило называется правилом Рунге.

Однако при применении правила Рунге необходимо учитывать величину погрешности вычислений: с уменьшением  абсолютная погрешность вычислений интеграла увеличивается (зависимость  от  обратно пропорциональная) и при достаточно малых  может оказаться больше погрешности метода. Если превышает , то для данного шага применять правило Рунге нельзя и желаемая точность не может быть достигнута. В таких случаях необходимо увеличивать значение .

При выводе правила Рунге вы существенно пользовались предположением, что . Если имеется только таблица значений , то проверку  «на постоянство» можно сделать непосредственно по таблице Дальнейшее развитие приведенных алгоритмов позволяет перейти к адаптивным алгоритмам, в которых за счет выбора различного шага интегрирования в разных частях отрезка интегрирования в зависимости от свойств  уменьшается количество вычислений подынтегральной функции.

Другая схема уточнения значений интеграла - процесс Эйтнена. Производится вычисление интеграла с шагами , причем . Вычисление значений . Тогда               (14).

За меру точности метода Симпсона принимают величину :

Примеры

Пример 1. Вычислить интеграл  по формуле Симпсона, если  задана таблицей. Оценить погрешность.

Таблица 3.

	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8
	1	0.995	0.98	0.955	0.921	0.878	0.825	0.765	0.697

Решение: Вычислим по формуле (1) при  и  интеграл .

.

По правилу Рунге получаем  Принимаем .

Пример 2. Вычислить интеграл .

Решение: Имеем 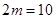. Отсюда h= =0.1. Результаты вычислений приведены в таблице 4.

Таблица 4.

Вычисление интеграла по формуле Симпсона

i
0	0		y0=1,00000
1	0.1	0,90909
2	0.2		0,83333
3	0.3	0,76923
4	0.4		0,71429
5	0.5	0,66667
6	0.6		0,62500
7	0.7	0,58824
8	0.8		0,55556
9	0,9	0,52632
10	1,0		0,50000=yn
å		3,45955(s1)	2,72818(s2)

По формуле Симпсона получим:

Подсчитаем погрешность полученного результата. Полная погрешность  складывается из погрешностей действий  и остаточного члена . Очевидно:

= ;

где - коэффициенты формулы Симпсона и e- максимальная ошибка округления значений подынтегральной функции.

 = .

Оценим остаточный член. Так как , то . Отсюда max при  и, следовательно, £ . Таким образом, предельная полная погрешность есть R=  и, значит, ± .

Пример3. Вычислить интеграл: .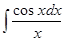

Решение:

2	-0,41613	-0,208065	1
2,05	-0,46107	-0,224912
2,1	-0,59485	-0,240405	4
2,15	-0,54736	-0,254586
2,2	-0,58850	-0,267500	2
2,25	-0,62817	-0,279187
2,3	-0,66628	-0,289687	4
2,35	-0,70271	-0,299026
2,4	-0,73739	-0,307246	2
2,45	-0,77023	-0,314380
2,5	-0,80114	-0,320465	4
2,55	-0,83005	-0,325510
2,6	-0,85689	-0,329573	2
2,65	-0,88158	-0,332672
2,7	-0,90407	-0,334841	4
2,75	-0,92430	-0,336109
2,8	-0,94222	-0,336507	2
,85	-0,95779	-0,336067
2,9	-0,97096	-0,334814	4
2,95	-0,98170	-0,332780
3	-0,98999	-0,329997	1

.

Поскольку ,  при xÎ[2,3], для производных  и  получаем:

-1.4 £  £1, то есть ç ê£ 1,

-£ £ 3, то есть ç ê£ 3.

Оценки для погрешности  метода Симпсона :  £ 0.0000017 для =0.1,  £ 0.0000002 для =0.05.

Чтобы погрешность округления не искажала столь точный результат для формулы Симпсона, все вычисления проводились с шестью знаками после запятой.

Окончательные результаты:

0,1	-0,30335	0,0000017
0,05	-0,30335	0,0000002