Домашних заданий и контрольных работ

Занятие 1-2. Общие вопросы аксиоматики. Проверка требований, предъявляемых к аксиомам.

Вопросы для обсуждения:

1. Сущность аксиоматического построения геометрии. Определение математической структуры.

2. Основные требования, предъявляемые к системе аксиом, методы проверки выполнения этих требований.

Задачи

I. Задана структура рода группы:

База: символ 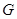, обозначающий непустое множество.

Отношения: 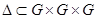 – тернарное отношение, определяющее отображение 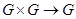. Если 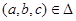, то будем записывать .

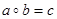Аксиомы:

.

.

.

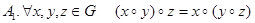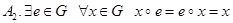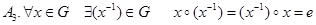Доказать: а) аксиома 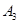 не зависит от аксиом  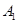и ;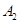

б) аксиома 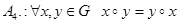, – не зависит от аксиом  – .

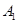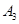II. Задана структура конечной проективной плоскости порядка :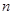

База: символы 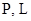, обозначающие непустые множества, элементы которых будем называть соответственно точками и прямыми.

Отношения: 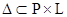 – отношение принадлежности. Если 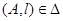, то будем говорить, что точка  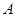лежит на прямой 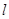, или прямая  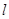проходит через точку 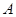, и записывать .

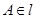Аксиомы:

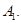 Для любых двух различных точек существует единственная прямая, проходящая через эти точки.

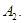 Для любых двух различных прямых существует единственная общая точка.

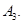 Существуют хотя бы четыре различные точки, никакие три из которых не лежат на одной прямой.

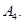 Каждой прямой принадлежит точно  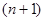точек, где  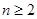и 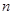 – некоторое натуральное число.

1. Проверить, что конфигурация Фано является моделью конечной проективной плоскости порядка 2.

, ,

; ; ;

; ; ;

.

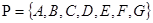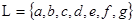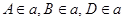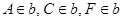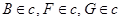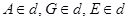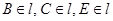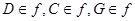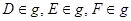2. Доказать независимость аксиом 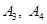 от остальных аксиом конечной проективной плоскости.

III. Определен род структур:

База: символы 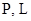, обозначающие непустые множества, элементы которых будем называть соответственно точками и прямыми.

Отношения: 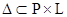 – отношение принадлежности.

Аксиомы:

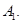 Каждая прямая есть множество точек.

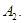 Для любых двух различных точек существует прямая, проходящая через эти точки, и притом только одна.

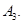 На каждой прямой лежит, по крайней мере, две точки.

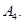 Существуют, по крайней мере, три точки, не лежащие на одной прямой.

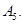 Для любой прямой  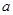и любой точки 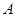, не лежащей на этой прямой, существует прямая, проходящая через точку  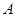и не пересекающая прямую .

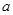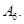 Для любой прямой  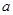и любой точки 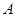, не лежащей на этой прямой, существует не более одной прямой, проходящей через точку 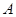, и не пересекающей прямую .

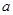1. Выяснить, какие из аксиом 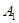 –  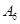выполняются в следующей модели:

, , , , .

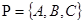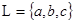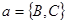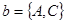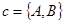2. Выяснить, какие из аксиом 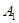 –  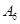выполняются в следующей модели:

, , , .

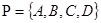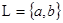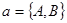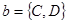3. Доказать непротиворечивость системы аксиом  – .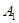

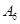4. Выяснить вопрос о независимости аксиом системы  – .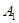

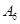IV. Определен род структур:

База: символы 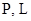, обозначающие непустые множества, элементы которых будем называть соответственно точками и прямыми.

Отношения: 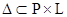 – отношение принадлежности.

Аксиомы:

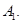 На каждой прямой лежит, по крайней мере, две точки.

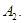 Для любых двух различных точек существует прямая, проходящая через эти точки, и притом только одна.

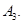 Существуют, по крайней мере, три точки, не лежащие на одной прямой.

1. Доказать непротиворечивость системы аксиом  – .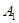

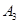2. Доказать независимость аксиом 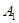, , 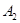 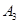от остальных аксиом системы.

 

Занятие 3. Аксиоматика Вейля евклидовой плоскости.

1. Определить структуру евклидовой плоскости в схеме Вейля.

2. Доказать непротиворечивость аксиоматики Вейля евклидовой плоскости.

3. Определить в схеме Вейля прямую, отрезок, луч, полуплоскость, параллельные и перпендикулярные прямые, параллелограмм, окружность, круг.

4. Доказать, что существуют три точки, не лежащие на одной прямой.

5. Доказать, что существуют пары прямых, проходящих через общую точку.

6. Доказать теорему косинусов.

7. Доказать теорему о средней линии треугольника.

8. Доказать, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

9. Доказать, что прямые, содержащие высоты треугольника, пересекаются в одной точке.

Занятие 4. Контроль остаточных знаний.

Занятие 5-6. Предложения, эквивалентные V постулату Евклида относительно аксиом Гильберта абсолютной геометрии.

На занятии обсуждаются доклады студентов с доказательствами эквивалентности относительно системы аксиом Гильберта абсолютной геометрии V постулата Евклида и каждого из следующих предложений [11], [15]:

1. Две прямые, не пересекающиеся между собой, образуют с любой третьей секущей их прямой равные соответственные углы.

2. Предложение Плейфера: Через точку, не лежащую на прямой, проходит не более одной прямой, не пересекающей данную прямую.

3. Предложение Лежандра: Перпендикуляр и наклонная к прямой всегда пересекаются.

4. Предложение Вольфганга Бойяи: Через три точки, не лежащие на одной прямой, можно провести окружность.

5. Сумма углов всякого треугольника равна двум прямым углам.

6. Предложение Посидония: В плоскости существуют, по меньшей мере, три точки, равноотстоящие от данной прямой и лежащие на одной прямой.

7. Предложение Валлиса: В плоскости существует хотя бы одна пара неравных, подобных треугольников.

8. Предложение Насир-Эддина: Если в простом четырехугольнике 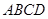 углы при основании  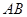прямые, а угол при вершине  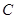острый, то .

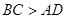9. Предложение Лежандра: Через всякую внутреннюю точку угла можно провести прямую, пересекающую обе стороны угла.

Занятие 7-8. Различные варианты обоснования школьного курса геометрии.

Обсуждение докладов студентов с обзором аксиоматик А.Н. Колмогорова, А.В. Погорелова, А.Д. Александрова школьного курса геометрии [1], [3], [4], [5], [7], [14], [16], [17].

Занятие 9. Интерпретация Пуанкаре плоскости Лобачевского [11], [15], [18].

Доклады студентов.

 

Занятие 10. Элементы геометрии Лобачевского.

Доклады студентов с доказательствами следующих утверждений на плоскости Лобачевского:

1. Вписанный в окружность угол, опирающийся на диаметр, острый.

2. Вписанные в окружность углы, опирающиеся на одну и ту же дугу, не равны.

3. Длина отрезка, соединяющего середины двух сторон треугольника, больше половины длины третьей стороны.

4. В прямоугольном треугольнике величина хотя бы одного из острых углов меньше, чем .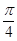

5. В прямоугольном треугольнике с острым углом 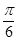, катет, лежащий против этого угла, больше половины гипотенузы.

 

Занятие 11-13. Геометрии Кэли-Клейна на плоскости.

Обсуждение докладов студентов по следующим темам:

1. Схема Кэли и Клейна мероопределения расстояний на прямой и углов в пучке прямых. Девять геометрий Кэли-Клейна на плоскости [12], [19].

2. Модель, свойства параллельных прямых, метрические соотношения между элементами треугольника, формулы движений, циклы в каждой из следующих геометрий на плоскости:

1) евклидова геометрия; 2) геометрия Галилея; 3) псевдоевклидова геометрия Минковского; 4) эллиптическая геометрия Римана; 5) гиперболическая геометрия Лобачевского; 6) дважды гиперболическая геометрия Лобачевского; 7) антиевклидова геометрия; 8) антипсевдоевклидова геометрия; 9) антигиперболическая геометрия.

Вариант тестового задания