 |
Главная |
Свойства размерности конечных упорядоченных множеств
|
из
5.00
|
Свойство монотонности: А Í В Þ d(A) £ d(B) для любых конечных упорядоченного множества В и его непустого подмножества А.
Доказательство:

Пусть < B, ≤ >- конечное упорядоченное множество размерности n. Имеем,  для линейных порядков £i на В. На подмножестве А рассмотрим индуцированный порядок
для линейных порядков £i на В. На подмножестве А рассмотрим индуцированный порядок  из В, т.е. ограничение отношения £ на А.
из В, т.е. ограничение отношения £ на А.
Рассмотрим ограничения линейных порядков £i на А – они также линейны и в пересечении дадут порядок  .
.
Значит, по определению размерности упорядоченного множества размерность <A,  > не превосходит n.
> не превосходит n.
Ч.т.д.
Свойство размерности дизъюнктивного объединения: Пусть А и В – конечные упорядоченные множества и X =A 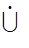 B . Тогда d(X)=max(d(A), d(B)), если хотя бы одно из множеств А или В не является цепью, и d (X )=2, если А и В – цепи.
B . Тогда d(X)=max(d(A), d(B)), если хотя бы одно из множеств А или В не является цепью, и d (X )=2, если А и В – цепи.
Доказательство:
 Дизъюнктивным объединением упорядоченных множеств А и В (А
Дизъюнктивным объединением упорядоченных множеств А и В (А 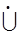 В) называется упорядоченное множество, состоящее из непересекающихся объединяемых множеств, на каждом из которых сохраняется свой порядок, а элементы из разных множеств попарно несравнимы.
В) называется упорядоченное множество, состоящее из непересекающихся объединяемых множеств, на каждом из которых сохраняется свой порядок, а элементы из разных множеств попарно несравнимы.
Пусть <A, £> и <B,  > - конечные упорядоченные множества.
> - конечные упорядоченные множества.
Порядок на А  для линейных порядков £i , а порядок на В
для линейных порядков £i , а порядок на В  для линейных порядков
для линейных порядков  .
.
Пусть для определённости n³m и n³2.
В результате объединения А и В получается упорядоченное множество, состоящее из всех элементов А и всех элементов В. Значит, одному линейному порядку на А 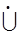 В соответствует два линейных порядка: один для А £i и один для В
В соответствует два линейных порядка: один для А £i и один для В  . Линейные порядки на А
. Линейные порядки на А 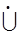 В должны содержать все n линейных порядков £i и все m линейных порядков
В должны содержать все n линейных порядков £i и все m линейных порядков  , чтобы в пересечении они дали множество А
, чтобы в пересечении они дали множество А 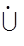 В.
В.
Первый линейный порядок на А 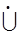 В определим следующим образом:
В определим следующим образом:
£1 …  .
.
Т.е. мы взяли первый линейный порядок на А и приписали к нему справа первый линейный порядок на В.
Второй линейный порядок на А 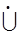 В получим, взяв из множества А линейный порядок £2, а из множества В, если m³2, то линейный порядок
В получим, взяв из множества А линейный порядок £2, а из множества В, если m³2, то линейный порядок  , если же m=1, то линейный порядок
, если же m=1, то линейный порядок  . Но сейчас линейный порядок из множества А поместим за линейным порядком из множества В, для того, чтобы элементы из разных множеств были попарно несравнимы:
. Но сейчас линейный порядок из множества А поместим за линейным порядком из множества В, для того, чтобы элементы из разных множеств были попарно несравнимы:
 … £2, где j=1 при m=1 и j=2 при m³2.
… £2, где j=1 при m=1 и j=2 при m³2.
Аналогичным образом будем получать остальные линейные порядки на А 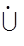 В:
В:
£i … 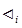 при i£m
при i£m
£i …  при i>m.
при i>m.
Получим n линейных порядков, пересечение которых даёт множество А 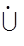 В. Т.е.
В. Т.е.  =n=max(d(A), d(B)).
=n=max(d(A), d(B)).
Ч.т.д.
Теорема 2. Размерность прямого произведения двух конечных упорядоченных множеств А и В меньше либо равна сумме их размерностей:
 .
.
Доказательство:
Дадим сначала несколько определений.
Пусть даны конечные упорядоченные множества <А, £> и <В, £>, размерности которых соответственно равны m и n. Поэтому  , для некоторых линейных порядков £i на А и
, для некоторых линейных порядков £i на А и  для линейных порядков на В.
для линейных порядков на В.
Определим покоординатно порядок на  :
:
(a, b)<(c, d) Û (a < c и b £ d) или (a £ c и b < d).
Определим m линейных порядков на  по первой компоненте:
по первой компоненте:
(a, b)<i(c, d) Û a<i c или (a=c и b<1 d) для i=1,…,m. (*)
Аналогично определим n линейных порядков на  по второй компоненте:
по второй компоненте:
(a, b)<j(c, d) Û b<j d или (b=d и a<1 c) для j=1,…,n. (**)
Исходя из этих определений, порядок на  можно определить и следующим образом:
можно определить и следующим образом:
(a, b)<(c, d)Û(a<ic и b£j d ) или (a£I c и b<j d) (***)
для i=1,…,m и для j=1,…,n.
Для завершения доказательства достаточно показать, что имеет место равенство:

Тогда по определению размерности конечного упорядоченного множества получим 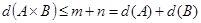 .
.
Требуется доказать, что для любых (a,b) и (c,d) из  :
:
(a, b)<(c, d) Û(a, b)<i(c, d) и (a, b)<j(c, d).
Для " (a,b) и (c,d) из  не умоляя общности, будем считать, что
не умоляя общности, будем считать, что
(a, b)<(c, d)  (a<I c и b£j d) или (a£I c и b<j d) для i=1,…,m и для j=1,…,n.
(a<I c и b£j d) или (a£I c и b<j d) для i=1,…,m и для j=1,…,n.
Отсюда вследствие того, что x£y выполняется тогда и только тогда, когда x<y или x=y, следует равносильность:
Û(a<I c и b<j d) или (a<I c и b=d) или (a=c и b<j d)
для i=1,…,m и для j=1,…,n
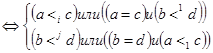


для i=1,…,m и для j=1,…,n.
Эта система равносильна тому, что элементы (a,b) и (c,d) сравнимы как по первой, так и по второй компоненте. И порядок на  равен пересечению его линейных порядков.
равен пересечению его линейных порядков.
А т.к. размерность – это наименьшее число линейных порядков, дающих в пересечении множество, то  .
.
Ч.т.д.
Теорема 3. Если А и В – не одноэлементные множества, причём А- решётка, а В –цепь, то размерность их прямого произведения на единицу больше размерности решётки:
 .
.
Доказательство:

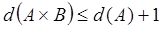 (по теореме 2).
(по теореме 2).
Покажем, что выполняется и 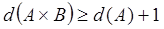 .
.
Возьмём любую цепь Z из множества цепей, пересечение которых образует решётку. Каждой такой цепи (а их  ) во множестве цепей, пересечение которых образует множество
) во множестве цепей, пересечение которых образует множество 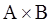 , будет соответствовать своя цепь, все первые компоненты которой находятся в таком же соответствии, как и элементы цепи Z .
, будет соответствовать своя цепь, все первые компоненты которой находятся в таком же соответствии, как и элементы цепи Z .
Но во множестве 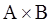 среди вторых компонент должны сохраняться и соотношения, которые присутствуют в цепи В. Значит, во множестве цепей, пересечение которых образует множество
среди вторых компонент должны сохраняться и соотношения, которые присутствуют в цепи В. Значит, во множестве цепей, пересечение которых образует множество 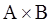 , появится еще одна цепь.
, появится еще одна цепь.
Ч.т.д.
Теорема 4. 
 решётка X , размерности n .
решётка X , размерности n .
Доказательство:
Возьмём n не одноэлементных цепей А1, А2,…,Аn и рассмотрим множество X=A1 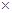 A2
A2 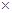 …
… 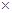 An=
An=  . (n-1) раз применяя теорему 3 получаем, что d(X)=n.
. (n-1) раз применяя теорему 3 получаем, что d(X)=n.
Ч.т.д.
Теорема 5. Размерность множества всех подмножеств ß ( M ) множества М равна мощности множества М, т.е.
d ( ß ( M ))=  .
.
Доказательство:
1) Покажем, что ß(M) @  , где D={0,1}.
, где D={0,1}.
 - будем рассматривать, как множество n-ок, состоящих из 0 и 1.
- будем рассматривать, как множество n-ок, состоящих из 0 и 1.
М={1,2,3,…,n}.

2) Чтобы доказать, что ß(M) и  изоморфны, нужно установить взаимно однозначное соответствие.
изоморфны, нужно установить взаимно однозначное соответствие.
Т.е. нужно показать, что для любого подмножества X множества М существует n-ка, состоящая из 0 и 1. И для любой n-ки существует подмножество Y множества М.
3) Выделим во множестве М подмножество X и составим по нему n-ку таким образом:
на место 1-ой компоненты n-ки поставим 1, если первый элемент множества М входит и в его подмножество X;
и 0, если 1-ый элемент множества М не входит в подмножество X.
Аналогичным образом определим все остальные компоненты n-ки.
Из нашего примера:

 X (0,1,1,0,1,0…0)
X (0,1,1,0,1,0…0)
n компонент
4) И, наоборот, возьмём произвольную n-ку. Например, (0,1,0,1,0…0). И поставим ей в соответствие подмножество Y множества М по тому же принципу:
если к-ая компонента равна 1, то к-ый элемент множества М входит в подмножество Y;
если же к-ая компонента равна 0, то к-ый элемент множества М не входит в подмножество Y.
Из примера получаем подмножество Y={2,4}.
5) Т.о. из ß(M)@  следует, что d(ß(M))=d(
следует, что d(ß(M))=d(  )
)  n
n
Получили, что d(ß(M))=  .
.
Ч.т.д.
Литература
1. Беран Л. Упорядоченные множества: Популярные лекции по математике. Вып. 55. – М.: Наука, 1981.
2. Биркгоф Г. Теория решёток. – М.: Наука, 1984.
3. Вечтомов Е. М. Теория решёток: учебно-методическая разработка спецкурса. – Киров: КГПИ, 1995.
4. Гретцер Г. Общая теория решёток. – М.: Мир, 1982.
5. Оре О. Теория графов. - М.: Наука, 1980.
|
из
5.00
|
Обсуждение в статье: Свойства размерности конечных упорядоченных множеств |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

