Фазовые переходы второго рода. Критическое поведение

Исследование влияния линейных дефектов структуры на критическое поведение трехмерной модели Гейзенберга

На степень бакалавра прикладных математики и физики

Направление 511600 - Прикладные математика и физика

Заведующий кафедрой:

профессор В.В. Прудников

Научный руководитель:

профессор В.В. Прудников

 

 

Омск - 2010

Оглавление

 

Введение

Глава 1. Фазовые переходы второго рода, компьютерное моделирование критического поведения

1.1 Фазовые переходы второго рода. Критическое поведение

1.2 Влияние дефектов структуры на критическое поведение

1.3 Теоретическая модель и алгоритмы компьютерного моделирования

1.3.1 Модель Гейзенберга

1.3.2 Алгоритм Вульфа

1.3.3 Метод коротковременной динамики

Глава 2. Результаты моделирования критического поведения трехмерной модели Гейзенберга с линейными дефектами

2.1 Алгоритм Вульфа. Определение критической температуры

2.2 Метод коротковременной динамики. Уточнение критической температуры. Расчет критических индексов

Заключение

Список литературы

Введение

 

Развитие вычислительных машин открыло новую область теоретической физики - компьютерное моделирование. Это позволяет исследовать поведение различных физических систем, описание которых традиционным способом громоздко или невозможно.

В настоящее время построенная теория упорядоченных конденсированных сред существенно использует идеальность их структуры и не может быть перенесена без существенных изменений на структурно неупорядоченные системы, к которым относятся: кристаллы с примесями, сплавы, аморфные тела и др. Реальные макроскопические системы всегда содержат дефекты структуры. Важнейшими из задач остаются разработка теоретических моделей для описания поведения неупорядоченных систем и исследование их свойств экспериментальным путём.

В данной работе исследуется критическое поведение ферромагнетика с примесями немагнитных атомов в виде случайно распределенных линий, т.е. с дефектами, обладающими квазидальним порядком (корреляционная функция распределения немагнитных атомов убывает по степенному закону G (r) ~ | r |-a с показателем a=2).

В работе [1] проведено теоретико-полевое исследование критического поведения трехмерных систем с дальней пространственной корреляцией дефектов. В ней показано, что дефекты, обладающие свойством дальней пространственной корреляции, изменяют критическое поведение не только систем с однокомпонентным параметром порядка, но и систем с двухкомпонентным (XY-модель) и трехкомпонентным (Гейзенберговская модель) параметром порядка.

Данная работа посвящена моделированию критического поведения трехмерной модели Гейзенберга с линейными дефектами. Основной целью ставилась разработка алгоритмов Метрополиса и Вольфа для данной модели, а затем определение критической температуры перехода в ферромагнитное состояние, и численное определение критических индексов характеризующих основные особенности данных неупорядоченных систем.

Глава 1. Фазовые переходы второго рода, компьютерное моделирование критического поведения

Фазовые переходы второго рода. Критическое поведение

 

Фазой называется физически однородная часть системы, отличающаяся своими физическими свойствами от других ее частей и отделённая от них четко выраженной границей [2]. Фазовый переход - это, соответственно, процесс перехода системы из одной фазы в другую. Различают фазовые переходы 1-го и 2-го рода. Основной особенностью фазовых переходов второго рода является непрерывное изменение при переходе плотности и внутренней энергии, внутренняя энергия и плотность вещества - первые производные химического потенциала, но при этом терпят разрыв теплоемкость и восприимчивость - вторые производные химического потенциала. При фазовом переходе второго рода происходит резкое нарушение симметрии системы, т.е. из высоко симметричной фазы в области высоких температур, система при охлаждении переходит в фазу с низкой симметрией.

Для количественной характеристики фазовых переходов второго рода вводят понятие параметра порядка [2]. Параметром порядка называется любая макроскопическая величина, зависящая от температуры следующим образом:

 

 

где Tc - температура фазового перехода.

В точке фазового перехода аномально возрастают флуктуации параметра порядка. Для выяснения характера флуктуаций вводят корреляционную функцию флуктуаций параметра порядка G, и величину, называемую корреляционной длиной . При приближении к критической точке корреляционная длина растет и в этой точке становится бесконечной. Крупномасштабные флуктуации приводят к сингулярностям в наблюдаемых макроскопических характеристиках системы.

Для характеристики макроскопических параметров системы, терпящих разрыв при температуре T= Tc, вводят понятие критических индексов, описывающих поведение величин вблизи критической точки [3]. Дадим общее определение критического показателя, описывающего поведение некоторой функции f (t) вблизи критической точки.

 

 

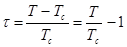
Здесь t - безразмерная переменная, измеряющая степень удаления температуры от критической. Предположим, что функция f (t) положительна и непрерывна для достаточно малых положительных значений, а также, что существует предел:

 

 

Этот предел, обозначенный буквой l, получил название критического показателя степени (или просто критического показателя), связанного с функцией f (t). Для краткости можно писать , чтобы подчеркнуть тот факт, что l критический показатель функции f (t). Критический показатель, конечно, дает значительно меньшую информацию, чем вид полной функции, но вблизи критической точки поведение функции, имеющей вид многочлена, определяют главным образом ее ведущие члены. Поэтому логарифмические кривые, полученные из эксперимента при температурах, достаточно близких к критической точке, имеют вид прямых, и критический показатель легко найти из наклона этих прямых. Таким образом, критические показатели всегда измеримы, чего нельзя сказать о полной функции. Вторая причина такого внимания к критическим показателям заключается в том, что имеется большое число соотношений между критическими показателями, которые выводятся из общих термодинамических и статистических положений, и поэтому справедливы для любой частной системы. Существует простая однозначная связь между критическим показателем и качественным поведением рассматриваемой функции вблизи критической точки t=0. Если критический показатель l отрицателен, то соответствующая функция f (t) вблизи критической точки расходится к бесконечности; положительные же значения l соответствуют функции f (t), обращающейся в этой точке в нуль. Чем меньше l, тем “резче” поведение f (t) в том смысле, что для отрицательных l расходимость становится сильнее, а для положительных l кривая идет к нулю более круто.

Итак, для характеристики макроскопических параметров системы вводятся:

критический индекс , характеризующий поведение теплоемкости вблизи критической температуры:

 

 

индекс , для параметра порядка

 

 

индексы , характеризующие поведение восприимчивости:

 

 

индексы ν для характеристики корреляционной длины:

 

 

индекс 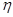 для корреляционной функции:

 

 

где D - размерность системы.

Можно ввести динамический критический индекс для описания поведения времени корреляций:

 

 

В действительности, не все перечисленные выше критические индексы являются независимыми. Между ними существуют следующие простые соотношения:

 

 

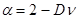
Таким образом, чтобы полностью описать критической поведение системы в равновесии, достаточно вычислить лишь какие-либо два статических критических индекса, а оставшиеся легко выражаются через них. Для описания динамики системы необходимо знать индекс z.

гейзенберг фазовый переход критический