Основные статистические параметры

В статистике существует ряд числовых характеристик, называемых параметрами распределения. В области управления качеством на практике используется их ограниченное количество. Далее будут рассмотрены некоторые из них.

1) Центр группирования. Одной из основных характеристик статистической совокупности, дающей представление о том, вокруг какого центра группируются все значения, является среднее арифметическое. Оно определяется из выражения:      

 ,

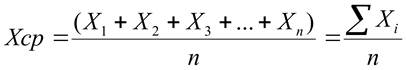где Х_i - измеренный параметр i-го члена совокупности, n - количество членов совокупности.

2) Величина рассеяния. Статические совокупности могут иметь близкие или даже одинаковые значения центра группирования, но отдельные значения величин в них могут существенно отличаться, вследствие того, что разброс значений относительно центра бывает разный. Самой элементарной характеристикой рассеяния является вариационный размах R, определяемый по формуле

R = X_max - X_min,

 где Xmax, Xmin - максимальное и минимальное значения статистической совокупности.

Вариационный размах не всегда характерен, так как учитывает только крайние значения, которые могут сильно отличаться от всех других значений. Более точно рассеяние определяется с помощью показателей, учитывающих отклонение всех значений от среднего арифметического. Основным из этих показателей является среднее квадратичное отклонение результата наблюдений, которое определяется по формуле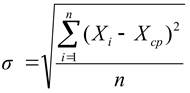

Это отклонение является наиболее распространенным и общепринятым показателем вариации. Величина под корнем, то есть σ², называется дисперсией. Дисперсия имеет самостоятельное значение во многих задачах математической статистики и относится к числу важнейших показателей вариации.

 Показателем отклонения значения самого среднего арифметического является среднее квадратическое отклонение среднего значения S, которое еще называют среднее квадратическое отклонение результата измерения.           

3) Форма распределения вероятности. Для характеристики формы распределения обычно используют ту математическую модель, которая наилучшим образом приближает к виду кривой распределения вероятностей, полученной при анализе экспериментально полученных данных.

4) Закон нормального распределения. Большинство случайных явлений, происходящих в жизни, в частности, в производстве и научных исследованиях, характеризуются наличием большого числа случайных факторов, описывается законом нормального распределения, который является основным во многих практических исследованиях. Однако нормальное распределение не является единственно возможным. В зависимости от физической природы случайных величин, некоторые из них на практике могут иметь распределение другого вида, например, логарифмическое, экспоненциальное, Вейбулла, Симпсона, Релея, равной вероятности и др.

Уравнение, описывающие плотность вероятности нормального распределения имеет вид:         

Нормальное распределение характеризуется двумя параметрами μ и σ² и на графике представляет собой симметричную кривую Гаусса (рисунок 1), имеющую максимум в точке соответствующей значению Х = μ (соответствует среднему арифметическому Х_ср и называется центром группирования), а при Х → -∞ и Х → ∞ асимптотически приближающуюся к оси абсцисс. Точка перегиба кривой находится на расстоянии σ от центра расположения μ. С уменьшением σ кривая растягивается вдоль оси ординат и сжимается вдоль оси абсцисс. Между абсциссами μ - σ и μ + σ расположено 68,3 % всей площади кривой нормального распределения. Это означает, что при нормальном распределении 68,3% всех измеренных единиц отклоняются от среднего значения не более чем на σ, то есть все они находятся в пределах + σ. Площадь, заключенная между ординатами, проведенными на расстоянии 2σ с обеих сторон от центра составляет 95,4 % и соответственно столько же единиц совокупности находится в пределах μ+2σ. И наконец, 99,73 % всех единиц находится в пределах μ+3σ. Это так называемое правило «трех сигм», характерное для нормального распределения. Согласно этому правилу за пределами отклонения на 3σ находится не более 0,27 % всех значений величин, то есть 27 реализаций на 10 тысяч. В технических приложениях принято при оценке результатов измерений работать с коэффициентами z при σ, соответствующим 90%, 95%, 99%, 99,9% вероятности попадания результата в область допуска.

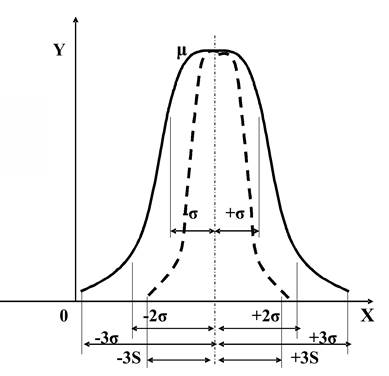
Рисунок 1 – Кривая Гаусса

Следует отметить, что это же правило распространяется на отклонения среднего значения Х_ср. Оно также колеблется в некоторой области на три значения среднего квадратического отклонения среднего значения S в обе стороны, и в этой области заключено 99,73 % всех значений среднего значения. Нормальное распределение хорошо проявляется при большом количестве членов статистической совокупности, не менее 30.

5) Распределение Стьюдента. Для практики большой интерес представляет возможность судить о распределении случайных величин и определять производственные погрешности во всех изготовленных изделиях и погрешности научных экспериментов по результатам измерения параметров статистической совокупности полученным из партии малого объема. Эта методика была разработана Карлом Госсетом в 1908 году и опубликована под псевдонимом Стьюдент.

Распределение Стьюдента симметрично, но более сплющено, чем кривая нормального распределения, и поэтому вытянуто на концах (рисунок 2). Для каждого значения n имеется своя t-функция и свое распределение. Коэффициент z заменен в распределении Стьюдента коэффициентом t, значение которого зависит от заданного уровня значимости, который определяет какая часть реализации может находиться за пределами выбранной области кривой распределения Стьюдента и количества изделий в выборке.

Рисунок 2 – Кривая Стьюдента

При больших n распределение Стьюдента асимптотически сближается со стандартным нормальным распределением. С приемлемой для практики точностью можно считать, что при n=30, распределение Стьюдента, которое иногда называют t-распределением, апроксимируется нормальным.[4]

Корреляция