Интерполяционный полином Лагранжа.

Введение

В задачах теории колебаний, электродинамики и других разделах прикладной математики широко применяется аппроксимация функций при описании физических параметров сред. В задачах вычислительной математики аппроксимация функций является основой для разработки многих методов и алгоритмов.

Аппроксимация, или приближение — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми. Иными словами, аппроксимация некоторой функции y=f(x) заключается в замене другой функцией g(x, a₀,a­_1,…, a_n) так, чтобы отклонение g от f(x) удовлетворяло в некоторой области (на множестве Х) определенному условию.

При этом функция g(x, a₀,a­_1,…, a_n) обычно выбирается с учетом специфических особенностей рассматриваемой функции f(x). Если множество Х дискретно, то приближение называется точечным, если же Х есть отрезок a≤x≤b, то приближение называется интегральным.

Частным случаем аппроксимации является интерполяция.

Обычно задача аппроксимации распадается на две части:

1. Сначала устанавливают вид зависимости y=f(x) и, соответственно вид эмпирической формулы, то есть решают, является ли она линейной, квадратичной, логарифмической или какой-либо другой.

2. После этого определяются численные значения неизвестных параметров выбранной эмпирической формулы, для которых приближение к заданной функции оказывается наилучшим.

 

Иной подход к решению задачи аппроксимации:

- Если нет каких-либо теоретических соображений для подбора вида формулы, обычно выбирают функциональную зависимость из числа наиболее простых, сравнивая их графики с графиком заданной функции.

 

- После выбора вида формулы определяют ее параметры. Для наилучшего выбора параметров задают меру близости аппроксимации экспериментальных данных. Во многих случаях, в особенности если функция f(x) задана графиком или таблицей (на дискретном множестве точек), для оценки степени приближения рассматривают разности f(x)φ(x_i) для точек x₀, x₁, …, x_n.

 

Для практики важен случай аппроксимации функции многочленами, т.е.

 

F(x)=a₀+a₁x+a₂x²+…+a_nxⁿ                                             (1)

 

Интерполяционный полином Лагранжа.

1.1. Теоретические основы метода.

 

Интерполяционный полином Лагранжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n+1 пар чисел (x ₀ , y ₀ ),(x ₁ , y ₁ )… (x_n , y_n ), где все x_j различны, существует единственный многочлен L ( x ) степени не более n, для которого L ( x_j )= y_j.

Интерполяционный полином Лагранжа имеет вид:

 

где l_i ( x ) – базисные полиномы, определяющиеся по формуле:

 

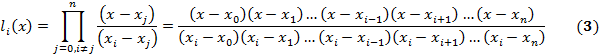
l_i ( x ) обладают следующими свойствами:

 

- являются многочленами степени n;

- l_i ( x_i ) =1;

- l_i ( x_j ) =0 при j ≠ i.

Отсюда следует, что L ( x ), как линейная комбинация l_i ( x ), может иметь степень не больше n, и L ( x_i )= y_i.

 

Оценку погрешности определяют по формуле:

 

 

| f ( x )- L_n ( x )| ≤ | L_{n +1} ( x )- L_n ( x ) |                                                                              (4)

 

Задание №1:

 

Выполнить интерполяцию таблично заданной функции y = f ( x ).

 

i	Х	Y
0	0.0	0.979498
1	0.1	1.060831
2	0.2	1.138837
3	0.3	1.213312
4	0.4	1.284076
5	0.5	1.350965
6	0.6	1.413842
7	0.7	1.472590
8	0.8	1.527116
9	0.9	1.577351

 

 

Вычислить значение интерполирующей функции в точке a=0.865. Оценить погрешность интерполяции.

 

1.2 Синтез полинома Лагранжа.

 

Перенумеруем узлы следующим образом: x ₀ – ближайший к заданной точке a узел и т.д.

i	Х	Y
0	0.9	1.577351
1	0.8	1.527116
2	0.7	1.472590
3	0.6	1.413842
4	0.5	1.350965
5	0.4	1.284076
6	0.3	1.213312
7	0.2	1.138837
8	0.1	1.060831
9	0.0	0.979498

Построим интерполяционный многочлен Лагранжа для n=2. В этом случае он будет иметь вид:

L ₂ (x)=l ₀ * y ₀ +l ₁ * y ₁ +l ₂ * y ₂.

 

l₀=  ;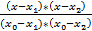

 

l₁= ;

l₂= ;

 

При увеличении порядка многочлена до n=4, полином Лагранжа будет выглядеть следующим образом:

 

L ₂ (x)=l ₀ * y ₀ +l ₁ * y ₁ +l ₂ * y ₂ +l ₃ * y ₃ +l ₄ * y ₄.

 

При этом, все базисные полиномы необходимо полностью пересчитать:

l ₀ =  ;

 

l ₁ =  ;

l ₂ =  ;

 

l ₃ =  ;

l ₄ =  ;

 

И, наконец, составим полином Лагранжа при n=9:

 

L ₂ (x)=l ₀ * y ₀ +l ₁ * y ₁ +l ₂ * y ₂ +l ₃ * y ₃ +l ₄ * y ₄ +l ₅ * y ₅ +l ₆ * y ₆ +l ₇ * y ₇ +l ₈ * y ₈ +l ₉ * y ₉.

 

Вновь пересчитываем базисные полиномы:

l ₀ =  ;

 

l ₁ =  ;

l ₂ =  ;

 

l ₃ =  ;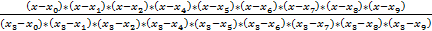

l ₄ =  ;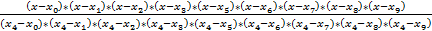

 

l ₅ =  ;

 

l ₆ =  ;

l ₇ =  ;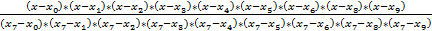

 

l ₈ =  ;

l ₉ =  .

 

Интерполяция полиномом Лагранжа возможна для произвольно заданных узлов интерполяции. Однако из приведенных выше расчетов видно, что добавление хотя бы одного нового узла интерполяции влечет за собой не только появление нового слагаемого, но и пересчет всех ранее вычисленных слагаемых.

Блок схема алгоритма интерполяции полиномом Лагранжа представлена на рис.1.

 

Входные данные:

- количество узлов интерполяции N;

- значение аргумента х в заданной точке;

- массив известных значений аргументов х(i) и функции y(i), сведенных в один двумерный массив arg(i,j). При этом, в связи с тем что значения аргументов изменяются в заданном диапазоне с равным интервалом, их значения вычисляются автоматически и записываются в первый столбец массива arg(i,1). Значения функции вводятся с клавиатуры и сохраняются во втором столбце (arg(i,2));

- порядок многочлена Лагранжа k.            

 

Выходные данные:

- массив табличных значений аргументов arg(i,1) и функции arg(i,2);

- массив значений многочленов Лагранжа L();

- погрешность вычислений Е.

 

Программа включает в себя функцию lagrange блок-схема алгоритма которой, представлена на рис. 2. Функция принимает входные данные: порядок полинома Лагранжа, значение аргумента в заданной точке, массив табличных значений аргументов и функции в виде двумерного массива. И возвращает значение многочлена Лагранжа порядка k в точке х.