 |
Главная |
Общие свойства интерполяционных пространств
|
из
5.00
|
Пусть A - векторное пространство над полем вещественных или комплексных чисел. Оно называется нормированным векторных пространством, если существует вещественнозначная функция (норма)  , определенная на A, удовлетворяющая условием.
, определенная на A, удовлетворяющая условием.
1)  , причем
, причем 
2)  (λ-скаляр)
(λ-скаляр)
3)  .
.
Пусть A и B – два нормированных векторных пространства. Отображение T из A в B называется ограниченным линейным оператором, если
 ,
,  и
и  .
.
Ясно, что всякий ограниченный линейный оператор непрерывен.
Пусть A0 и A1 – топологических векторных пространства. Говорят, что
A0 и A1 совместимы, если существует отделимое топологическое векторное пространство U, такое, что A0 и A1, являются подпространствами. В этом случае можно образовать сумму A0 + A1, и пересечение A0∩A1. Сумма состоит из всех a  U, представимых в виде a=a0+a1, где a0
U, представимых в виде a=a0+a1, где a0  A, и a1
A, и a1  A,
A,
Справедлива следующая лемма
Лемма 2.1. Пусть A0 и A1-совместимые нормированные векторные пространства. Тогда
A0∩A1, есть нормированное векторное пространство с нормой

A0 + A1, также представляет собой нормированное векторное пространство с нормой

При этом если A0 и A1 – полные пространства, то A0∩A1 и A0 + A1 также полны.
Дадим некоторые важные определения:
Категория σ состоит из объектов A,B,C…., и морфизмов R,S,T,…. между объектами и морфизмами определено трехместное отношение T: A↷B.
Если T: A↷B и S: B↷C, то существует морфизм ST, называемый произведением (или композицией) морфизмов S и T, такой, что ST: A↷ C.
Операция взятия произведения морфизмов удовлетворяет закону ассоциативности: T(SR)=(TS)R. далее, для всякого объекта A из σ существует морфизм I=IA, такой, что для любого морфизма T: A↷A TI=IT=T
Через σ1 обозначим категорию всех совместимых пар  пространств из σ.
пространств из σ.
Определение 2.1. Пусть  =(A0,A1)-заданная пара из σ1. Пространство A из σ будем называть промежуточным между A0 и A1 (или относительно
=(A0,A1)-заданная пара из σ1. Пространство A из σ будем называть промежуточным между A0 и A1 (или относительно  ), если имеют место непрерывные вложения.
), если имеют место непрерывные вложения.
 .
.
Если, кроме, того T:  ↷
↷  влечет T: A ↷ A, то A называется интерполяционным пространством между A0 и A1.
влечет T: A ↷ A, то A называется интерполяционным пространством между A0 и A1.
Более общим образом, пусть  и
и  - две пары из σ1. Тогда два пространства A и B из σ называются интерполяционными относительно
- две пары из σ1. Тогда два пространства A и B из σ называются интерполяционными относительно  и
и  соответственно и T:
соответственно и T:  ↷
↷  влечет T: A↷ B.
влечет T: A↷ B.
Если выполнено
 ,
,
В этом случае, говорят, что A и B равномерные интерполяционные пространства.
Определение 2.2 Интерполяционные пространства A и B называются пространствами типа θ (0≤θ≤1), если

В случае с=1 говорят, что A и B - точные интерполяционные пространства типа θ.
3. О норме и спектральном радиусе неотрицательных матриц
Хорошо известно, что проблема нахождения нормы линейного оператора, спектрального радиуса оператора являются трудной проблемой и в конечномерном случае. В то же время, иногда важно не вычисляя нормы оператора знать, как она изменится в случае некоторого преобразования.
В данной работе изучается влияние распределения ненулевых элементов неотрицательной матрицы на норму соответствующего оператора и спектрального радиуса.
Определим пространство  как множество всех наборов вида
как множество всех наборов вида
a=(a1, a2,…, aN)
с нормой
 .
.
Множество Q={(k,l):k,l=1,…,N} назовем решеткой размерности N x N. Любое множество Q0={(ki,lj):  ,
,  } будет являться подрешеткой размерности r x m.
} будет являться подрешеткой размерности r x m.
Спектральный радиус линейного оператора в конечномерном пространстве 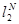 определяется следующим образом:
определяется следующим образом:
r(A)=  ,
,
где lk- собственные значения оператора A.
Пусть m ≤ N, d1,…,dm - положительные числа. Через Dm обозначим множество неотрицательных матриц А, ненулевые элементы которых принимают значения d1,…,dm. Через P(A) обозначим множество индексов соответствующих положительным элементам. Пусть AÎDm. Если D={(ki,lj), i=1,…,q, j=1,…,p} подрешетка, содержащая P(A), то для соответствующего оператора А

Как видно из этого определения, от перестановки строк и столбцов матрицы норма не меняется.
Пусть даны положительные числа d1,…,dm и натуральное число m < N2.
Будем исследовать следующие вопросы:
Как расположить числа d1,…,dm в решетке Q, чтобы норма линейного оператора AQ соответствующего решетке (матрице) Q была максимальной?
Пусть в неотрицательной решетке Q m положительных элементов. Как расположить (m+1)-ый элемент, чтобы норма линейного оператора AQ соответствующей полученной решетке была максимальной?
Как расположить числа d1,…,dm в решетке Q, чтобы спектральный радиус был минимальным (максимальным)?
Справедливы следующие теоремы:
Теорема 3.1 Пусть d1,…,dm положительные числа, Dm - класс неотрицательных матриц, ненулевые элементы которых принимают значения d1,…,dm. Если m ≤ N, Q0 -произвольная подрешетка размерности 1  m, то
m, то
 .
.
Доказательство. Воспользуемся определением и неравенством Коши-Буняковского, получаем



Неравенство в обратную сторону очевидно.
Теорема доказана.
Данное утверждение говорит о том, что если ненулевых элементов меньше либо равно N, то своего максимума норма достигается когда все ненулевые элементы расположены в одной строке или в одном столбце.
Теорема 3.2 Пусть d1=…=dm=d, то есть Dm – множество всех матриц, имеющие m ненулевых элементов, которые равны числу d. Q0 -произвольная решетка, симметричная относительно главной диагонали размерности n  n, где n=min{r: r2 ≥ m}. Тогда
n, где n=min{r: r2 ≥ m}. Тогда
 ,
,
где [m1/2] - целая часть числа m1/2.
Доказательство. Из свойства спектрального радиуса имеем для AÎDm

 .
.
Пусть Q1 -подрешетка, также симметричная относительно главной диагонали размерности 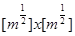 . Тогда для AÎDm, Q1ÌP(A)ÌQ0 имеет место представление
. Тогда для AÎDm, Q1ÌP(A)ÌQ0 имеет место представление
А=А1+А0, где А1,А0ÎDm, Р(А1)=Q1, P(A0)ÌQ1\Q0.
Учитывая, что матрицы А0 и А1 неотрицательны, получаем
 ,
,
поэтому r(A0)≤r(A).
С другой стороны А1 – симметричная матрица и следовательно
 .
.
Таким образом,
 .
.
Теорема доказана.
Теорема 3.3 Пусть множество GÌQ, где Q - решетка размерности n  n таково, что, если (k,l)ÎG, то (l,m),(n,k)ÏG для всех n,mÎ{1,2,…,N}.
n таково, что, если (k,l)ÎG, то (l,m),(n,k)ÏG для всех n,mÎ{1,2,…,N}.
Тогда, если P(A)ÌG, то r(P(A))=0.
Доказательство. Не трудно проверить, что для матрицы А с ненулевыми элементами из G (т.е. P(A)ÌG) имеет место равенство А2=0, т.е. А – нильпотентная матрица индекса 2 и следовательно у нее единственное собственное значение 0.
Теорема доказана.
Теорема 3.4 Пусть AÎDm. Пусть Q0 -минимальная подрешетка содержащая P(A), (Q0ÉP(A)) такая, что в каждой строке и в каждом столбце находится хотя бы один элемент соответствующий нулевому элементу матрицы A.
Пусть Ad – матрица, полученная из матрицы A добавлением элемента со значением d>0 в одно из свободных мест, тогда

Доказательство.
Так как норма оператора не зависит от перестановки строк и столбцов матрицы, то можно считать, что решетка A0={(i,j), i=1,…,l; j=1,…,m} расположена в левом верхнем углу матрицы A. Пусть добавлен еще один ненулевой элемент d с координатами (i0,j0) вне решетки Q0. Возможны три случая:
1) 1 ≤ i0 ≤ l, j0 > m;
2) i0 > l, 1 ≤ j0 ≤ m;
3) i0 > l, j0 > m.
Рассмотрим первый случай. Не уменьшая общности положим, что этот ненулевой элемент соответствует индексу (1, m+1). По условию теоремы в каждой строке и в каждом столбце имеется хотя бы один нулевой элемент и мы можем предположить, что a1m=0. Получаем:



Используя неравенства
 ,
, 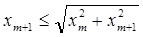
имеем:

Пусть z1=x1, z2=x2,…,zm=  и
и
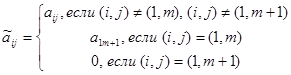 ,
,
тогда


где элемент  имеет координаты (1,m).
имеет координаты (1,m).
Следовательно
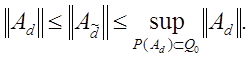
Рассмотрим второй случай. Пусть добавленный ненулевой элемент соответствует индексу (l+1,1). Учитывая, что в каждой строке и в каждом столбце решетки есть хотя бы один ненулевой элемент и то, что от перестановки строк норма матрицы не меняется, мы можем предположить, что al1=0. Аналогично первому случаю имеем:


 .
.
Используя неравенства
 ,
, 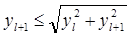
получаем:
 .
.
Пусть z1=y1, z2=y2,…,zm=  и
и
 ,
,
тогда


где элемент  имеет координаты (l,1). Следовательно
имеет координаты (l,1). Следовательно
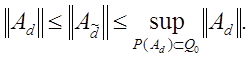
Рассмотрим последний случай. Не уменьшая общности положим, что этот ненулевой элемент соответствует индексу (l+1, m+1). В этом случае нужно учесть, что от перестановки строк и столбцов норма матрицы не изменится, поэтому можно положить, что alm=0. Рассуждая также, как и в предыдущих случаях, получаем:



где элемент  имеет координаты (l,m).
имеет координаты (l,m).
Теорема доказана. Аналогичные задачи для интегральных операторов были рассмотрены в работах [1], [5].
4. Некоторые интерполяционные свойства семейств конечномерных пространств
Пусть 1 ≤ p < ∞, 1 ≤ q ≤ ∞. Определим семейство конечномерных пространств:

где  невозрастающая перестановка последовательности
невозрастающая перестановка последовательности  . Обозначим через
. Обозначим через  –множество всех непустых подмножеств из {1,2,...N} Пусть M
–множество всех непустых подмножеств из {1,2,...N} Пусть M 
 , 1 ≤ p < ∞, 1 ≤ q ≤ ∞, множество M назовем сетью.
, 1 ≤ p < ∞, 1 ≤ q ≤ ∞, множество M назовем сетью.
Определим семейство конечномерных пространств


|e| - количество элементов множества e.
При q=∞ положим
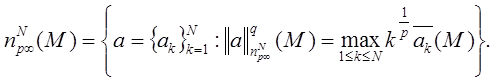
Данные пространства являются конечномерными аналогами сетевых пространств, введенных в [1].
Будем говорить что {AN} ↪ {BN} если существует константа c, такая что  для любого
для любого  , где c не зависит от
, где c не зависит от  .
.
Лемма 4.1 Пусть 1 ≤ q <q1≤ ∞, 1 ≤ p ≤ ∞,  . Тогда имеет место вложение
. Тогда имеет место вложение
 ↪
↪ 
то есть

где с не зависит от выбора N.
Доказательство. Пусть 
 (1)
(1)
то есть  ↪
↪ 
Теперь рассмотрим случай, когда 1 ≤ q <q1< ∞, и воспользуемся неравенством (1)


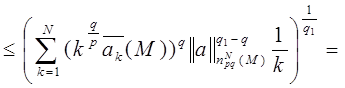


Лемма доказана.
Лемма 4.2 Пусть 1≤p<p1<∞, 1≤q,q1≤∞. Тогда имеем место вложение
 ↪
↪ 
Доказательство.
Согласно условию леммы, нам достаточно доказать вложения при p < p1 :
 ↪
↪ 
Получаем:



Лемма доказана.
Лемма 4.3 Пусть 1<p<∞, 1≤q≤∞, M=  . Тогда
. Тогда


Равенства понимаются с точностью до эквивалентности норм, причем константы не зависят от 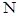 .
.
Доказательство. Сначала докажем соотношение:
 (2)
(2)
Заметим, что

Поэтому

Теперь покажем обратное неравенство. Пусть  . Учитывая выбор
. Учитывая выбор 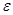 имеем.
имеем.


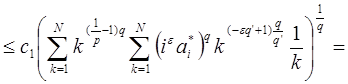
 ~
~
~ 
Заметим, что


Согласно (2) получаем:

то есть  ↪
↪  .
.
Докажем обратное включение. Пусть 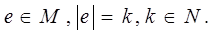 Введем следующие обозначения:
Введем следующие обозначения:

Тогда
 .
.
Пусть для определенности
 .
.
Возможны следующие случаи:
 .
.
В первом случае получаем, что

 .
.
Во втором случае 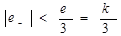 , следовательно
, следовательно  . Представим
. Представим  , тогда
, тогда  . Здесь и далее
. Здесь и далее  - целая часть числа
- целая часть числа  .
.
Получаем

Заметим, что существует  такое, что
такое, что

Положим  Тогда
Тогда  .
.
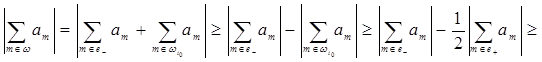
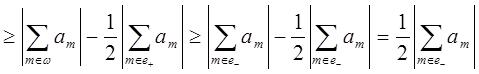 .
.
Таким образом, получаем

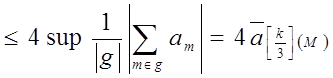
Из того, что

Имеем

То есть  . Следовательно
. Следовательно 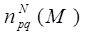 ↪
↪  где соответствующие константы не зависят от N.
где соответствующие константы не зависят от N.
Лемма доказана.
Для пары пространств  определим интерполяционные пространства
определим интерполяционные пространства  аналогично [5] .
аналогично [5] .
Пусть 
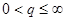 , тогда
, тогда

где 
При q=∞

Лемма 4.4 Пусть 
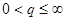 , d>1. Тогда
, d>1. Тогда


Справедлива следующая
Теорема 4.1 Пусть ≤p0<p1<∞, 1<q0,q1≤∞, M – произвольная сеть. Тогда
 ↪
↪ 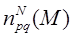
где 
Доказательство.
Учитывая, что 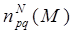 ↪
↪  нам достаточно, доказать следующее вложение
нам достаточно, доказать следующее вложение
 ↪
↪ 

Пусть  Рассмотрим произвольное представление a=a0+a1, где
Рассмотрим произвольное представление a=a0+a1, где
 тогда
тогда


 (3)
(3)
Так как представление a=a0+a1 произвольно, то из (3) следует

Где 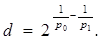 Рассматривая норму элемента в пространстве и применяя
Рассматривая норму элемента в пространстве и применяя
лемму 4.4 , получаем:

Теорема доказана.
Теорема 4.2 Пусть 1≤p0<p1<∞, 1<q0,q1≤∞,  Тогда имеет место равенство
Тогда имеет место равенство

Это равенство понимается в смысле эквивалентности норм с константами, не зависящими  N.
N.
Доказательство. По теореме 4.1 и того, что  является обобщением пространств Лоренца нам достаточно доказать следующее вложение:
является обобщением пространств Лоренца нам достаточно доказать следующее вложение:
 ↩
↩ 
 .
.
Определим элементы  и
и  следующим образом
следующим образом

 , тогда
, тогда 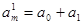 .
.
Заметим что
 (4)
(4)
где 
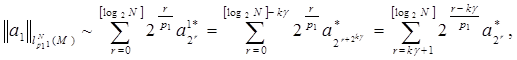 (5)
(5)
где 
Тогда

Из (4) и (5) имеем:


Оценим отдельно каждое из слагаемых последнего равенства, используя неравенство Гельдера:
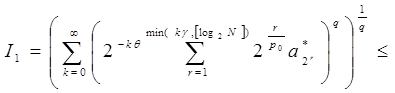
 ~
~



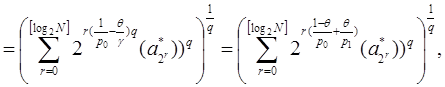
где  .
.
Таким образом, получаем, что  Аналогично рассмотрим второе слагаемое:
Аналогично рассмотрим второе слагаемое:

 ~
~
~ 

 ~
~ 
Таким образом, получаем

где c не зависит от  .
.
Теорема доказана.
Теорема 4.3 Пусть  - матрица
- матрица 

 , тогда
, тогда
 ~
~ 
Причем соответствующие константы не зависят от 
Доказательство.
Воспользуемся эквивалентными представлением нормы 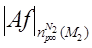 и неравенством о перестановках, получим
и неравенством о перестановках, получим
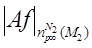 ~
~ 
где 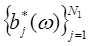 - невозрастающая перестановка последовательности
- невозрастающая перестановка последовательности 
Применим неравенство Гельдера

Учитывая лемму 3, имеем

Обратно, пусть e произвольное множество из M1,  , где
, где

Тогда
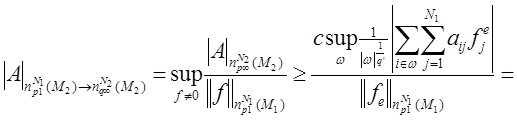

В силу произвольности выбора e из M1 получаем требуемый результат.
Следствие. Пусть  - матрица
- матрица 


p0<p1, q0<q1, 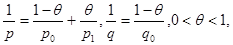 тогда
тогда
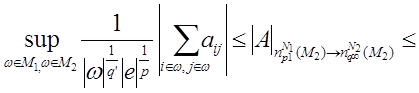

Доказательство. Из теоремы 3 следует, что


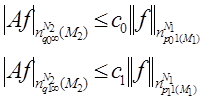
Воспользуемся интерполяционными теоремами 1,2, получаем

то есть

С другой стороны по лемме 1 и теореме 3 имеем

 ,
,
Следствие доказано.
Заключение
В данной курсовой работе приведены и доказаны некоторые свойства конечномерных пространств, а именно пространств Лоренца и сетевых пространств.
Полученные результаты могут быть полезны для студентов, магистрантов, аспирантов и преподавателей. Кроме того, данный материал может быть использован для чтения спецкурсов и спецсеминаров.
Список использованной литературы
1. Берг Й., Лефстрем Й. Интерполяционные пространства. Введение. М.: Мир, 1980.
2. Гохберг И.Ц., Крейн М.Г. Введение в теорию линейных несамосопряженных операторов. М.: Наука, 1965.
3. Костюченко А.Г., Нурсултанов Е.Д. Об интегральных операторах в пространствах. Фундаментальная и прикладная математика. Т.5. №2, 1999. С. 475-491.
4. Костюченко А.Г., Нурсултанов Е.Д. Теория управления катастрофами. //Успехи математических наук, 1998. Т.53. Выпуск 2.
5. Нурсултанов Е.Д. Сетевые пространства и неравенства типа Харди-Литтлвуда //Матем.сборник.-1998.-Т.189, №3.-С.83-102.
6. Таджигитов А.А. О зависимости нормы матрицы от взаимного расположения ее элементов. // Материалы Международной научной конференции "Современные проблемы теории функций и их приложения", Саратов, Россия, 2004, с. 177-178.
7. Таджигитов А.А. О норме и спектральном радиусе неотрицательных матриц. //Материалы Международной научно-практической конференции "Современные исследования в астрофизике и физико-математических науках", Петропавловск, 2004, с. 104-107.
8. Таджигитов А.А. Интерполяционные свойства конечномерных пространств. //Международная научная конференция студентов, аспирантов и молодых ученых "Ломоносов 2005", Астана, 2005, с. 41-42.
|
из
5.00
|
Обсуждение в статье: Общие свойства интерполяционных пространств |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

