Сложный процентный рост

В Сберегательном банке России для некоторых видов вкладов принята следующая система начисления денег. За первый год нахождения внесенной суммы на счете начисляется 40% от нее. В конце года вкладчик может снять со счета эти деньги – «проценты», как их обычно называют.

Если же он этого не сделал, то они присоединяются к начальному вкладу, и поэтому в конце следующего года 40% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.

Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк1000 руб. и ни разу не будет брать деньги со счета:

40% от 1000 руб. составляют 0,4 * 1000 = 400 руб., и следовательно, через год на его счете будет

1000 + 400 = 1400 (руб.)

40% от новой суммы 1400 руб. составляют 0,4 * 1400 = 560 руб., и следовательно, через 2 года на его счете будет

1400 + 560 = 1960 (руб.)

40% от новой суммы 1960 руб. составляют 0,4 * 1960 = 784 руб., и следовательно, через 3 года на его счете будет

1960 + 784 = 2744 (руб.)

Нетрудно представить себе, сколько при таком непосредственном , «лобовом» подсчёте понадобилось бы времени для нахождения суммы вклада через 10 лет. Между тем, подсчёт можно вести значительно проще.

Именно через год начальная сумма увеличится на 40%, то есть составит 140% от начальной, или, другими словами, увеличится в 1,4 раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 40%. Следовательно, через 2 года начальная сумма увеличится в 1,4 * 1,4 = 1,4² раза.

Еще через один год и эта сумма увеличится в 1,4 раза, так что начальная сумма увеличится в 1,4 * 1,4² = 1,4³ раза. При таком способе рассуждения получаем решение нашей задачи значительно более простое:

1,4³ * 1000 = 2,744 * 1000 = 2744 (руб.)

Решим теперь эту задачу в общем виде. Пусть банк начисляет p% годовых, внесённая сумма равна S рублей, а сумма, которая будет на счёте через n лет, равна S_n рублей.

p%  от S составляют S рублей, и через год на счёте окажется сумма

S₁ = S

то есть начальная сумма увеличится в 1 +  раза.

За следующий год сумма S₁ увеличится во столько же раз, и поэтому через два года на счёте будет сумма

S₂ = (1 + ) S₁ = (1 + ) (1+ ) S =(1 +  )² S.

Аналогично, S₃ =(1 +  )³ S и так далее. Другими словами, справедливо равенство

S_n = (1 + ) ³ S.

Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.

Задача 1. Какая сумма будет на срочном счёте вкладчика через 4 года, если банк начисляет 10% годовых и внесённая сумма равна 2 000 рублей?

Решение.

Подставим в формулу значения процентной ставки p = 10, количество лет n = 4 и величину первоначального вклада S = 2000, получим:

(1 + )⁴  * 2000 = 1,1⁴ * 2000 = 1,4641 * 2000 = 2928,2 (рублей).

Ответ: через 4 года на счёте будет сумма 2928,2 рубля.

ТЕМА: ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ И ДИФФЕРЕНЦИАЛА

Найти производные от функций:

а) 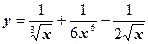;	б) ;	в) ;
г)	д) 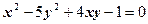;	е)

Решение. При решении заданий а)-в) применим следующие правила дифференцирования:

1) 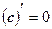;                                               2) ;

3) ;                                 4)

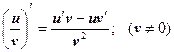5)                  6)

7)        ;          

8) если , т.е. 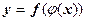- сложная функция, то .

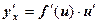       На основании определения производной и правил дифференцирования составлена таблица производных основных элементарных функций.

1 ,	8 ,
2 ,	9 ,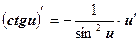
3 ,	10 ,
4 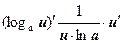,	11 ,
5 ,	12 ,
6 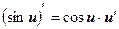,	13 .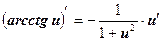
7 ,

Используя правила дифференцирования и таблицу производных, найдем производные данных функций:

а) .

Ответ:

б) .

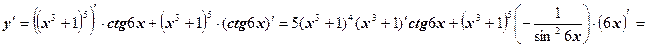
Ответ:

       в) .

Ответ:

ТЕМА: НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ