Энергетический спектр водородоподобного примесного центра и его волновая функция с учетом спина электрона в сильном магнитном поле

Целю данной работы, является теоретическое исследование магнитооптического поглощения комплексов квантовая точка – водородоподобный примесный центр в условиях сильного магнитного поля. Рассматривается случай как продольной, так и поперечной по отношению к направлению магнитного поля поляризации света. Расчет коэффициентов поглощения проводится для двух случаев: с учетом дисперсии размеров квантовой точки и учетом лоренцева уширения уровней энергии электрона.

Рассмотрим квантовую точку, находящуюся в продольном по отношению к оси Оz магнитном поле, содержащую мелкий водородоподобный примесный центр, расположенный в центре квантовой точки. Рассматривается случай сильного магнитного поля, когда магнитная длина aB много меньше эффективного боровского радиуса ad. Дальнейшие вычисления проводятся в цилиндрической системе координат с началом О в центре квантовой точке. Вектор магнитной индукции  направлен вдоль оси Оz ( ;  - орт оси Оz). Векторный потенциал магнитного поля  выберем в симметричной калибровке:

 

 , (2.1.1)

 

где 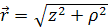 – значение радиус вектора, в случае сильного магнитного поля 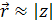,так как поле как бы «зашнуровывает» примесный центр в ρ направлении.

Для описания одноэлектронных состояний в квантовых точках используем потенциал конфайнмента в модели «жесткой стенки»

 

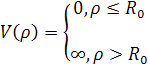 . (2.1.2)

 

Стационарные состояния электрона, локализованного на примесном центре, описываются уравнением Шредингера, записанном в виде

 

 , (2.1.3)

 

где 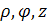 – цилиндрические координаты;

 – оператор Гамильтона (гамильтониан);

E – собственные значения гамильтониана;

 - собственные функции гамильтониана.

Гамильтониан в приближении эффективной массы для векторного потенциала (2.1.1) с учетом знака заряда электрона, в цилиндрических координатах выбранной модели запишется как

 

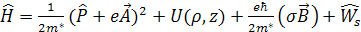 , (2.1.4)

 

где  - эффективная масса;

 - оператор обобщенного импульса;

 Кл – заряд электрона;

 - потенциал кулоновского взаимодействия;

 Дж·с – постоянная Планка;

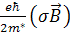 - энергия спинового магнитного момента электрона (сделаем поправку в конце расчетов так, как оно не имеет координатной зависимости);

 – спиновые матрицы Паули;

 – оператор спин-орбитального взаимодействия (учитывать не будем из-за малости данного взаимодействия по сравнению с энергией спинового магнитного момента электрона);

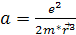 – коэффициент взаимодействия;

L – орбитальный момент электрона;

s – спиновой момент электрона.

Спиновые матрицы Паули имеют вид

 

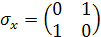; ;  . (2.1.5)

 

Потенциал кулоновского взаимодействия в случае сильного магнитного поля становится эффективно одномерным и определяется выражением

 

 , (2.1.6)

 

где ε – относительная диэлектрическая проницаемость среды,

ε0 = 8.85·10-12 Ф/м – электрическая постоянная.

Перепишем уравнение Шредингера (2.1.3) в модели «жесткой стенки» в приближении эффективной массы с учётом допущений. Получим

 

 . (2.1.7)

 

По правилу коммутаций оператора обобщенного импульса имеем

 , (2.1.8)

 

 коммутативны если

С учётом (2.1.8) уравнение Шредингера (2.1.7) примет вид

 

 . (2.1.9)

 

Распишем векторный потенциал 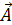 и оператор обобщённого импульса . Заметим, что магнитное поле направлено вдоль оси Оz, тогда

 

 . (2.1.10)

 

Учитывая (2.1.10), получим

 

 (2.1.11)

 

Решение уравнения (2.1.11) будем искать в виде

 

 , (2.1.12)

 

 , (2.1.13)

 

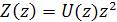 . (2.1.14)

Выбор именно такого вида функции  обусловлен тем, что  должна быть собственной функцией оператора

 

 , (2.1.15)

 

 , (2.1.16)

 

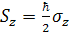 . (2.1.17)

 

Сделаем ряд следующих обозначений

 

 - эффективный боровский радиус, (2.1.18)

 

 – магнитная длина, (2.1.19)

 

 - циклотронная частота. (2.1.20)

 

С учётом (2.1.12) – (2.1.20) уравнение (2.1.11) запишется в виде

 

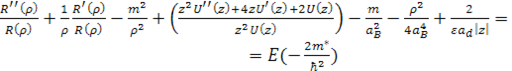(2.1.21)

 

Разделим в уравнении (2.1.21) переменные:

 

 (2.1.22)

 

где  - разделительный множитель.

Из (2.1.22) получим два уравнения

 

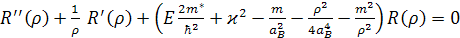 , (2.1.23)

 

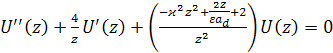 . (2.1.24)

 

Решение уравнений (2.1.23) и (2.1.24) приводит к результату

 

 , (2.1.25)

 

 . (2.1.26)

 

Таким образом, с учетом (2.1.13), (2.1.25) и (2.1.26) получим для волновой функции следующее выражение

 

 , (2.1.27)

 

где  - нормировочный множитель равный

 

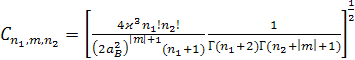 . (2.1.28)

 

Собственные значения гамильтониана определятся как

 

 . (2.1.29)

 

Энергетический спектр и волновые функции электрона локализованного на водородоподобном примесном центре (основное состояние(n1=0,m=0,n2=0)), принимая во внимание (2.1.27), (2.1.28) и (2.1.29) примут вид

 

 , (2.1.30)

 . (2.1.31)

 

На рисунке 1 представлен компьютерный анализ зависимости (2.1.31) энергетического спектра электрона находящегося в основном состоянии в квантовой точке на основе InSb от величины магнитной индукции.

Рисунок 1 – Зависимость энергии связи от величины магнитной индукции для соединения InSb

 

Как видно из рисунка величина энергии электрона локализованного на водородоподобном примесном центре линейно зависит от магнитной индукции.

Волновые функции и энергетический спектр конечного состояния системы квантовая точка – водородоподобный примесный центр после взаимодействия со световой волной можно представить в виде

 

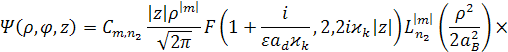
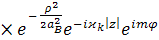 , (2.1.32)

 

где 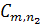 - нормировочный множитель равный

 

 , (2.1.33)

 

 , (2.1.34)