Теория случайных величин

Теория вероятностей

 

Элементы комбинаторики

 

Перестановкой называется определенное линейное расположение всех элементов некоторого множества. Число перестановок из n элементов обозначается  и равно .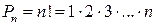

Размещением называется любой набор, содержащий m элементов этого множества, взятый в определенном линейном порядке. Число размещений из n элементов по  m обозначается  и равно: .

Сочетанием называется любой набор, содержащий m элементов этого множества, без учета их порядка. Число размещений из n элементов по m обозначается 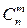 и равно: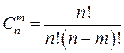

Понятие события

 

Событие- всякий факт, который в результате опыта может произойти или не произойти.

Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий.

Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий.

Случайным называют событие, которое при осуществлении совокупности условий может либо произойти, либо не произойти.

Несколько событий образуют полную группу событий в данном опыте, если в результате опыта непременно должно появиться хотя бы одно из них.

Несколько событий называют несовместными в данном опыте, если никакие два из них не могут появиться вместе.

Несколько событий называют равновозможными в данном опыте, если по условиям симметрии есть основание считать, что ни одно из этих событий не является объективно более возможным, чем другое.

События, которые обладают всеми тремя свойствами: образуют полную группу, несовместны и равновозможны называют элементарными исходами (элементарными событиями) или случаями.

Элементарный исход, который ведет к появлению события А, называют благоприятным исходом событию А. Событие A можно рассматривать как набор благоприятных ему исходов.

Множество всех элементарных исходов называют полным пространством событий.

 

Вероятность события (классическое определение вероятности)

 

Вероятность события - численная мера объективной возможности этого события.

Вероятность события   (если опыт сводится к схеме случаев) определяется формулой 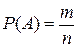 (классическая формула вероятности),

где - общее число элементарных исходов, - число благоприятных исходов событию .

Так как   заключено между 0 и , то .

Вероятность достоверного события , так как .

Вероятность невозможного события равна , так как .

 

       Пример. В коробке находится 10 шаров. 3 из них красные, 2 – зеленые, остальные белые. Найти вероятность того, что вынутый наугад шар будет красным, зеленым или белым.

 

       Появление красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара – событие А, появление зеленого – событие В, появление белого – событие С.

       Тогда, в соответствии с записанными выше формулами, получаем:

 

           

       Определение. Относительной частотой события А называется отношение числа опытов, в результате которых произошло событие А к общему числу опытов.

       Отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного произведения опытов, а относительная частота – после опыта.

       Так в рассмотренном выше примере, если из коробки наугад извлечено 5 шаров и 2 из них оказались красными, то относительная частота появления красного шара равна:

       Как видно, эта величина не совпадает с найденной вероятностью.

 

       При достаточно большом числе произведенных опытов относительная частота изменяется мало, колеблясь около одного числа. Это число может быть принято за вероятность события.

 

       Вообще говоря, классическое определение вероятности – довольно относительное.

       Это обусловлено тем, что на практике сложно представить результат опыта в виде совокупности элементарных событий, доказать, что события равновероятные.

       К примеру при произведении опыта с подбрасыванием монеты на результат опыта могут влиять такие факторы как несимметричность монеты, влияние ее формы на аэродинамические характеристики полета, атмосферные условия и т.д.

 

       Классическое определение вероятности неприменимо к испытаниям с бесконечным числом исходов. Чтобы преодолеть этот недостаток вводится понятие геометрической вероятности, т.е. вероятности попадания точки в какую – либо часть плоскости.

       Так, если область  является подобластью области , то вероятность попадания наугад взятой точки области  в подобласть  равна отношению .

 

Операции над событиями.

 

       Определение. События А и В называются равными, если осуществление события А влечет за собой осуществление события В и наоборот.

 

       Определение. Объединением или суммой событий А _k называется событие A, которое означает появление хотя бы одного из событий А _k.

       Определение. Пересечением или произведением событий A_k называется событие А, которое заключается в осуществлении всех событий A_k.

       Определение. Разностью событий А и В называется событие С, которое означает, что происходит событие А, но не происходит событие В.

       Определение. Дополнительным к событию А называется событие , означающее, что событие А не происходит.

       Определение. Элементарными исходами опыта называются такие результаты опыта, которые взаимно исключают друг друга и в результате опыта происходит одно из этих событий, также каково бы ни было событие А, по наступившему элементарному исходу можно судить о том, происходит или не происходит это событие.

       Совокупность всех элементарных исходов опыта называется пространством элементарных событий.

           

       Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

       Следствие 1: Если события  образуют полную группу несовместных событий, то сумма их вероятностей равна единице.

       Определение. Противоположными называются два несовместных события, образующие полную группу.

       Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

       Следствие 2: Сумма вероятностей противоположных событий равна единице.

       Определение. Событие А называется независимым от события В, вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

       Определение. Вероятность события В, вычисленная при условии, что имело место событие А, называется условной вероятностью события В.

       Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.

       Также можно записать:

       Если события независимые, то , и теорема умножения вероятностей принимает вид:

       В случае произведения нескольких зависимых событий вероятность равна произведению одного из них на условные вероятности всех остальных при условии, что вероятность каждого последующего вычисляется в предположении, что все остальные события уже совершились.

 

       Пример. Из полной колоды карт (52 шт.) одновременно вынимают четыре карты. Найти вероятность того, что среди этих четырех карт будет хотя бы одна бубновая или одна червонная карта.

 

       Обозначим появление хотя бы одной бубновой карты – событие А, появление хотя бы одной червонной карты – событие В. Таким образом нам надо определить вероятность события С = А + В.

       Кроме того, события А и В – совместны, т.е. появление одного из них не исключает появления другого.

       Всего в колоде 13 червонных и 13 бубновых карт.

       При вытаскивании первой карты вероятность того, что не появится ни червонной ни бубновой карты равна , при вытаскивании второй карты - , третьей - , четвертой - .

       Тогда вероятность того, что среди вынутых карт не будет ни бубновых, ни червонных равна .

       Тогда

 

       Пример. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.

 

       Обозначим попадание в цель первым стрелком – событие А, вторым – событие В, промах первого стрелка – событие , промах второго – событие .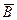

 

       Вероятность того, что первый стрелок попадет в мишень, а второй – нет равна

       Вероятность того, что второй стрелок попадет в цель, а первый – нет равна

Тогда вероятность попадания в цель только одним стрелком равна

Тот же результат можно получить другим способом – находим вероятности того, что оба стрелка попали в цель и оба промахнулись. Эти вероятности соответственно равны:

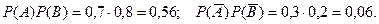
       Тогда вероятность того, что в цель попадет только один стрелок равна:

 

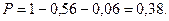
Формула полной вероятности.

 

       Пусть некоторое событие А может произойти вместе с одним из несовместных событий , составляющих полную группу событий. Пусть известны вероятности этих событий  и условные вероятности наступления события А при наступлении события H_i .

       Теорема. Вероятность события А, которое может произойти вместе с одним из событий , равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события А.

           

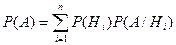
       Пример. Один из трех стрелков производит два выстрела. Вероятность попадания в цель при одном выстреле для первого стрелка равна 0,4, для второго – 0,6, для третьего – 0,8. Найти вероятность того, что в цель попадут два раза.

 

       Вероятность того, что выстрелы производит первый, второй или третий стрелок равна .

       Вероятности того, что один из стрелков, производящих выстрелы, два раза попадает в цель, равны:

       - для первого стрелка:

       - для второго стрелка:

       - для третьего стрелка:

       Искомая вероятность равна:

 

Формула Бейеса. (формула гипотез)

       Пусть имеется полная группа несовместных гипотез  с известными вероятностями их наступления . Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности .

       Требуется определить какие вероятности имеют гипотезы   относительно события А, т.е. условные вероятности .

       Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.

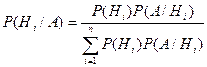
       Эта формула называется формулой Бейеса.

Повторение испытаний. Формула Бернулли

 

       Если производится некоторое количество испытаний, в результате которых может произойти или не произойти событие А, и вероятность появления этого события в каждом из испытаний не зависит от результатов остальных испытаний, то такие испытания называются независимыми относительно события А.

       Допустим, что событие А наступает в каждом испытании с вероятностью Р(А)=р. Определим вероятность Р_т,п того, что в результате п испытаний событие А наступило ровно т раз.

       Эту вероятность в принципе можно посчитать, используя теоремы сложения и умножения вероятностей, как это делалось в рассмотренных выше примерах. Однако, при достаточно большом количестве испытаний это приводит к очень большим вычислениям. Таким образом, возникает необходимость разработать общий подход к решению поставленной задачи. Этот подход реализован в формуле Бернулли.

       Пусть в результате п независимых испытаний, проведенных в одинаковых условиях, событие А наступает с вероятностью Р(А) = р, а противоположное ему событие  с вероятностью .

       Обозначим A_i – наступление события А в испытании с номером i. Т.к. условия проведения опытов одинаковые, то эти вероятности равны.

       Если в результате п опытов событие А наступает ровно т раз, то остальные п-т раз это событие не наступает. Событие А может появиться т раз в п испытаниях в различных комбинациях, число которых равно количеству сочетаний из п элементов по т. Это количество сочетаний находится по формуле:

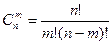
       Вероятность каждой комбинации равна произведению вероятностей:

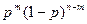
Применяя теорему сложения вероятностей несовместных событий, получаем формулу Бернулли:

       Формула Бернулли важна тем, что справедлива для любого количества независимых испытаний, т.е. того самого случая, в котором наиболее четко проявляются законы теории вероятностей.

           

       Пример. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятность того, что в цель попали не менее трех раз.

 

       Вероятность не менее трех попаданий складывается из вероятности пяти попаданий, четырех попаданий и трех попаданий.

       Т.к. выстрелы независимы, то можно применить формулу Бернулли вероятности того, что в т испытаниях событие в вероятностью р наступает ровно п раз.

 

       В случае пяти попаданий из пяти возможных:

       Четыре попадания из пяти выстрелов:

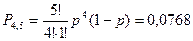
       Три попадания из пяти:

Окончательно, получаем вероятность не менее трех попаданий из пяти выстрелов:

 

Теория случайных величин

 

Случайные величины.

 

       Выше рассматривались случайные события, являющиеся качественной характеристикой случайного результата опыта. Для получения количественной характеристики вводится понятие случайной величины.

 

       Определение. Случайной величиной называется величина, которая в результате опыта может принимать то или иное значение, причем заранее известно какое именно.

       Случайные величины можно разделить на две категории.

 

       Определение. Дискретной случайной величиной называется такая величина, которая в результате опыта может принимать определенные значения с определенной вероятностью, образующие счетное множество (множество, элементы которого могут быть занумерованы).

Это множество может быть как конечным, так и бесконечным.

       Например, количество выстрелов до первого попадания в цель является дискретной случайной величиной, т.к. эта величина может принимать и бесконечное, хотя и счетное количество значений.

 

       Определение. Непрерывной случайной величиной называется такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка.

       Очевидно, что число возможных значений непрерывной случайной величины бесконечно.

 

       Для задания случайной величины недостаточно просто указать ее значение, необходимо также указать вероятность этого значения.

 

Закон распределения дискретной случайной величины.

 

       Определение. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины.

       Закон распределения может быть задан аналитически, в виде таблицы или графически.

       Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.

       Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.

 

Биноминальное распределение.

 

       Если производится п независимых испытаний, в каждом из которых событие А может появиться с одинаковой вероятностью р в каждом из испытаний, то вероятность того, что событие не появится, равна q = 1 – p.

       Примем число появлений события в каждом из испытаний за некоторую случайную величину Х.

           

Чтобы найти закон распределения этой случайной величины, необходимо определить значения этой величины и их вероятности.

           

Значения найти достаточно просто. Очевидно, что в результате п испытаний событие может не появиться вовсе, появиться один раз, два раза, три и т.д. до п раз.

           

Вероятность каждого значения этой случайной величины можно найти по формуле Бернулли.

       Эта формула аналитически выражает искомый закон распределения. Этот закон распределения называется биноминальным.

 

Распределение Пуассона.

 

       Пусть производится п независимых испытаний, в которых появление события А имеет вероятность р. Если число испытаний п достаточно велико, а вероятность появления события А в каждом испытании мало (p£0,1), то для нахождения вероятности появления события А k раз находится следующим образом.

 

       Сделаем важное допущение – произведение пр сохраняет постоянное значение:

 

       Практически это допущение означает, что среднее число появления события в различных сериях испытаний (при разном п) остается неизменным.

       Формула распределения Пуассона :

       Если известны числа l и k, то значения вероятности можно найти по соответствующим таблицам распределения Пуассона.

 

Числовые характеристики дискретных случайных величин.

 

       Закон распределения полностью характеризует случайную величину. Однако, когда невозможно найти закон распределения, или этого не требуется, можно ограничиться нахождением значений, называемых числовыми характеристиками случайной величины. Эти величины определяют некоторое среднее значение, вокруг которого группируются значения случайной величины, и степень их разбросанности вокруг этого среднего значения.

 

       Определение. Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на их вероятности.

 

       Математическое ожидание существует, если ряд, стоящий в правой части равенства, сходится абсолютно.

 

       С точки зрения вероятности можно сказать, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.

 

Свойства математического ожидания.

1) Математическое ожидание постоянной величины равно самой постоянной.

2) Постоянный множитель можно выносить за знак математического ожидания.

3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

Это свойство справедливо для произвольного числа случайных величин.

4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых.

       Это свойство также справедливо для произвольного числа случайных величин.

 

       Пусть производится п независимых испытаний, вероятность появления события А в которых равна р.

       Теорема. Математическое ожидание М(Х) числа появления события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.

       Однако, математическое ожидание не может полностью характеризовать случайный процесс. Кроме математического ожидания надо ввести величину, которая характеризует отклонение значений случайной величины от математического ожидания.

       Это отклонение равно разности между случайной величиной и ее математическим ожиданием. При этом математическое ожидание отклонения равно нулю. Это объясняется тем, что одни возможные отклонения положительны, другие отрицательны, и в результате их взаимного погашения получается ноль.

       Определение. Дисперсией (рассеиванием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

 

Вычисление дисперсии.

 

       Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания.

Свойства дисперсии.

 

 

1) Дисперсия постоянной величины равна нулю.

2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.

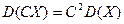
3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.

4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.

Справедливость этого равенства вытекает из свойства 2.

 

       Теорема. Дисперсия числа появления события А в п независимых испытаний, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в каждом испытании.

 

Среднее квадратическое отклонение.

 

       Определение. Средним квадратическим отклонением  случайной величины Х называется квадратный корень из дисперсии.

 

       Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин.

 

Функция распределения.

 

       Во всех рассмотренных выше случаях случайная величина определялась путем задания значений самой величины и вероятностей этих значений.

       Однако, такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, ее значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально.

       Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Рассмотренный только что пример даже при относительно простом условии (приборов только четыре) приводит к достаточно неудобным вычислениям, а если в задаче будет несколько сотен приборов?

       Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.

           

       Пусть х – действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее х, т.е. Х < x, обозначим через F(x).

 

       Определение. Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х.

       Функцию распределения также называют интегральной функцией.

Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.

       Для дискретной случайной величины функция распределения имеет вид:

       Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.

       Функция распределения дискретной случайной величины Х разрывна и возрастает скачками при переходе через каждое значение х _i.

 

Свойства функции распределения..

 

1) значения функции распределения принадлежат отрезку  [0, 1].

2) F(x) – неубывающая функция.

 при

3) Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b) , равна приращению функции распределения на этом интервале.

4) На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице.

5) Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.

       Таким образом, не имеет смысла говорить о каком – либо конкретном значении случайной величины. Интерес представляет только вероятность попадания случайной величины в какой – либо интервал, что соответствует большинству практических задач.

 

Плотность распределения.

 

       Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси.

 

       Определение. Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f( x) – первая производная от функции распределения F(x).

 

       Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.

       Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.

       После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины.

 

       Определение.  Случайная величина Х называется непрерывной, если ее функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением( может быть, конечного числа точек.

 

       Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина Х примет значение, принадлежащее заданному интервалу.

 

       Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу ( a, b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b.

       Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми x= a и x= b.

 

       Функция распределения может быть легко найдена, если известна плотность распределения, по формуле:

 

Свойства плотности распределения.

 

1) Плотность распределения – неотрицательная функция.

2) Несобственный интеграл от плотности распределения в пределах от - ¥ до ¥ равен единице.

 

Числовые характеристики непрерывных случайных величин.

 

       Пусть непрерывная случайная величина Х задана функцией распределения f( x). Допустим, что все возможные значения случайной величины принадлежат отрезку [a, b].

 

       Определение. Математическим ожиданием  непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл

       Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:

       При этом, конечно, предполагается, что несобственный интеграл сходится.

       Определение. Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.

       По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:

 

       Определение. Средним квадратичным отклонением называется квадратный корень из дисперсии.

 

       Определение. Модой М₀ дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.

       Если многоугольник распределения для дискретной случайной величины или кривая распределения для непрерывной случайной величины имеет два или несколько максимумов, то такое распределение называется двухмодальным или многомодальным.