 |
Главная |
Теория случайных величин
|
из
5.00
|
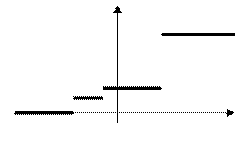
1. Дан графический закон распределения дискретной случайной величины (многоугольник распределения). Найти распределения случайной величины. Найти и построить функцию распределения случайной величины.
Деления по оси абсцисс на всех рисунках означает единичный отрезок
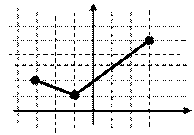
Решение:
Согласно представленному чертежу, значения случайной
величины -3, -1, 3.
Пусть одно деление на оси ординат равно 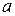 . Тогда значения
. Тогда значения
вероятностей, соответствующих значениям случайной
величины, равны 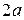 ,
, 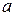 ,
, 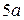 . Сумма вероятностей равна 1,
. Сумма вероятностей равна 1,
тогда 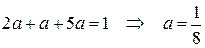 .
.
Таким образом, распределение случайной величины имеет вид:
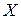
| -3 | -1 | 3 |
| 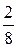
| 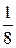
| 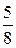
|
Функция распределения дискретной случайной величины имеет вид: 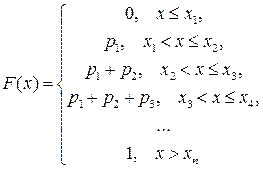 .
.
Для данного распределения 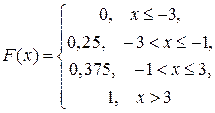
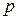
1
0,375
0,25
-3 -1 3 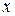
2. Дискретная случайная величина принимает значения 2, 5, 9 с соответствующими вероятностями 0,3, 0,1, 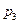 . Найти математическое ожидание случайной величины. Построить функцию распределения вероятностей.
. Найти математическое ожидание случайной величины. Построить функцию распределения вероятностей.
Решение:
Дополним ряд распределения, используя свойство 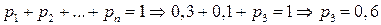 .
.
Полный ряд распределения:
| 2 | 5 | 9 |
| 0,3 | 0,1 | 0,6 |
Математическое ожидание 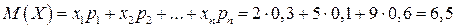 .
.
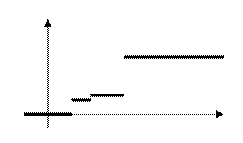 Для данного распределения
Для данного распределения 
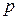
2 5 9 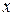
3. Дан ряд распределения случайной величины:
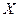
| -4 | 1 | 3 | 5 |
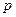
| 0,1 | 0,3 | 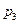
| 0,2 |
Найти моду случайной величины 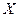 .
.
Решение:
Дополним ряд распределения, используя свойство 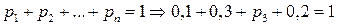 .
. 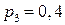 .
.
Полный ряд распределения:
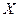
| -4 | 1 | 3 | 5 |
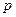
| 0,1 | 0,3 | 0,4 | 0,2 |
Мода случайной величины 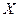 - наивероятнейшее значение случайной величины. Таким образом,
- наивероятнейшее значение случайной величины. Таким образом, 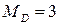 (значение вероятности 0,4 наибольшее).
(значение вероятности 0,4 наибольшее).
Ответ: 3.
4. Дан ряд распределения случайной величины 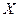 :
:
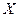
| 2 | 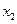
|
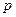
| 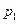
| 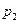
|
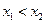 . Математическое ожидание
. Математическое ожидание 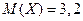 , дисперсия
, дисперсия 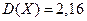 . Найти значение случайной величины
. Найти значение случайной величины 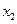 .
.
Решение:
Используя свойство для вероятностей, получим уравнение 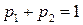 .
.
Используя формулу для математического ожидания, получим уравнение 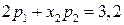 .
.
Используя формулу для дисперсии, получим уравнение 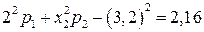 .
.
Получим систему уравнений:
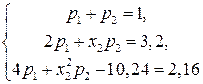
Из первого уравнения 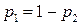 . Тогда система примет вид:
. Тогда система примет вид: 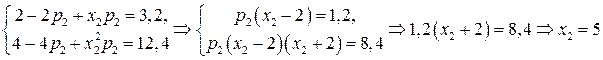 .
.
Ответ: 5.
5. В урне 2 белых и 3 черных шара. Шары извлекаются из урны без возвращения до появления черного шара. Случайная величина 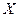 – количество извлеченных белых шаров. Найти ряд распределения случайной величины.
– количество извлеченных белых шаров. Найти ряд распределения случайной величины.
Решение:
Значения случайной величины: 0, 1, 2. Каждому значению случайной величины соответствует событие.
Событие 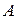 – при первом извлечении появился сразу черный шар (извлечено 0 белых),
– при первом извлечении появился сразу черный шар (извлечено 0 белых), 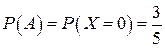 .
.
Событие 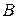 – при первом извлечении появился белый шар, а при втором извлечении появился черный шар (извлечен 1 белый),
– при первом извлечении появился белый шар, а при втором извлечении появился черный шар (извлечен 1 белый), 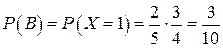 .
.
Событие 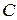 – при первом извлечении появился белый шар, при втором извлечении появился белый шар, а при третьем извлечении появился черный шар (извлечены 2 белых шара),
– при первом извлечении появился белый шар, при втором извлечении появился белый шар, а при третьем извлечении появился черный шар (извлечены 2 белых шара), 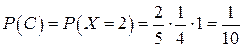 .
.
Ряд распределения рассматриваемой случайной величины имеет вид:
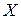
| 0 | 1 | 2 |
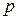
| 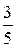
| 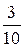
| 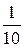
|
6. Стрелок производит 30 выстрелов по мишени. Вероятность попадания при одном выстреле 0,4. Случайная величина 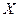 – количество попаданий. Найти математическое ожидание и дисперсию случайной величины.
– количество попаданий. Найти математическое ожидание и дисперсию случайной величины.
Решение:
Так как производится 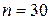 независимых испытаний, вероятность появления события А (попадание в цель) равна
независимых испытаний, вероятность появления события А (попадание в цель) равна 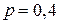 в каждом испытании, то случайная величина
в каждом испытании, то случайная величина 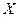 распределена по биномиальному закону. Тогда математическое ожидание и дисперсия вычисляются по формулам
распределена по биномиальному закону. Тогда математическое ожидание и дисперсия вычисляются по формулам 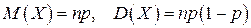 .Для рассматриваемой случайной величины
.Для рассматриваемой случайной величины 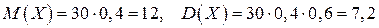 .
.
Ответ: 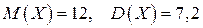 .
.
7. Дана функция распределения случайной величины 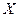 :
: 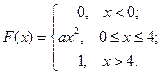
Найти параметр, функцию плотности и основные числовые характеристики.
Решение:
Используя свойство непрерывности функции распределения, имеем 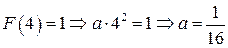 . Функция распределения имеет вид:
. Функция распределения имеет вид: 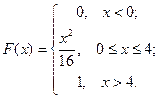 .
.
Функция плотности распределения вероятностей 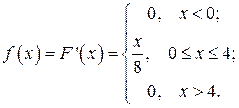 .
.
Основные числовые характеристики:
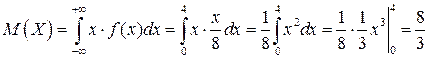 .
.
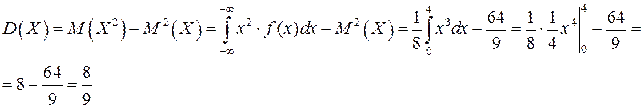
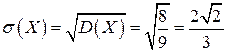 .
.
8. Случайная величина 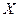 распределена по равномерному закону на отрезке [2; 10]. Найти вероятность попадания случайной величины в интервал
распределена по равномерному закону на отрезке [2; 10]. Найти вероятность попадания случайной величины в интервал 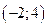 . Записать функции распределения и плотности. Найти основные числовые характеристики.
. Записать функции распределения и плотности. Найти основные числовые характеристики.
Решение:
Параметры распределения 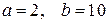 .
.
Числовые характеристики:
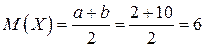
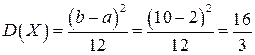
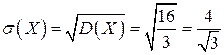
Функция распределения: 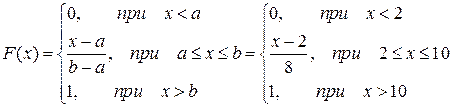
Функция плотности: 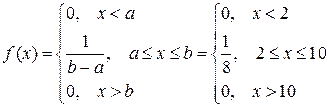
Вероятность: 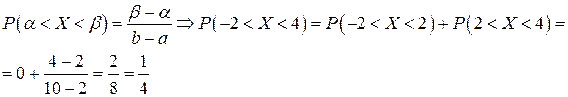
9. Случайная величина 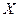 распределена по экспоненциальному закону с параметром
распределена по экспоненциальному закону с параметром 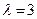 . Найти функцию распределения вероятностей и функцию плотности случайной величины. Определить числовые характеристики. Найти вероятность попадания случайной величины в интервал
. Найти функцию распределения вероятностей и функцию плотности случайной величины. Определить числовые характеристики. Найти вероятность попадания случайной величины в интервал 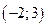 .
.
Решение:
Параметр распределения 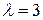 .
.
Числовые характеристики:
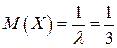
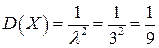
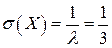
Функция распределения: 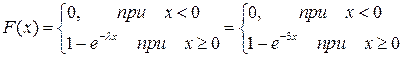
Функция плотности: 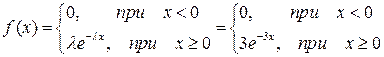
Вероятность: 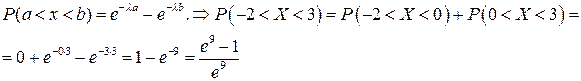
10. Закон распределения случайной величины 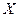 задан функцией плотности
задан функцией плотности 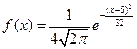 . Найти числовые характеристики случайной величины.
. Найти числовые характеристики случайной величины.
Решение:
Параметры распределения 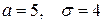 .
.
Числовые характеристики:
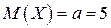
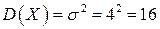
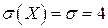
|
из
5.00
|
Обсуждение в статье: Теория случайных величин |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

