Некоторые свойства оператора набла

 

Ранее мы ввели оператор векторного дифференцирования

 

.

 

С помощью этого оператора мы записали основные дифференциальные операции в тензорных полях:

 

,

,

.

Оператор  является обобщением оператора дифференцирования и обладает соответствующими свойствами производной:

) производная суммы равна сумме производных

 

;

 

) постоянный множитель можно выносить за знак оператора

 

.

 

В переводе на язык векторных функций эти свойства имеют вид:

 

,

,

,

,

,

.

 

Выводятся эти формулы так же, как и соответствующие формулы для производных функции одной переменной.

Использование оператора Гамильтона позволяет упростить многие операции, связанные с дифференцированием в тензорных полях. Однако следует иметь в виду, что этот оператор векторный и с ним надо обращаться аккуратно. Рассмотрим некоторые применения этого оператора. При этом соответствующие формулы записываются как с помощью оператора Гамильтона, так и в обычных обозначениях.

1) ,

;

) ,

;

) ,

) ,

;

) ,

.

 

Доказательство этих равенств можно произвести как непосредственным вычислением соответствующих функций, так и с помощью оператора «набла». Рекомендуется самостоятельно проверить справедливость записанных равенств двумя методами.

В качестве примера, показывающего необходимость аккуратного обращения с оператором Гамильтона, вычислим градиент скалярного произведения двух векторных функций 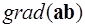. Формально, используя свойства оператора дифференцирования, можно записать

 

.

 

Если считать , , 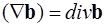то получим неправильный результат

 

.

Ошибка здесь заключается в том, что выражение  следует понимать как 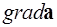, т.е. как градиент векторной функции (специального обозначения для этого объекта нет). Правильным будет выражение

 

,

 

где точка означает свертку тензора с вектором (свертка является обобщением понятия скалярного произведения). Более удобной здесь является тензорная форма записи

 

.

 

Здесь по повторяющимся индексам производится суммирование от 1 до 3.

 

Список литературы

скалярный поле дифференцирование кронекер

1. Тихонов А.Н., Самарский А.А. Уравнения математической физики, М.: МГУ, 1999, 798 с.

. Кальницкий Л.А., Добротин Д.А., Жевержев В.Ф. Специальный курс высшей математики для втузов, М.: «Высшая школа», 1976, 390 с.

. Берман Г.Н. Сборник задач по курсу математического анализа, М.: Наука, 1985, 384 с.

. Все решения к «Сборнику задач по общему курсу физики» В.С. Волькенштейн, М.: Аст, 1999, книга 1, 430 с., книга 2, 588 с.

. Красильников О.М. Физика. Методическое руководство по обработке результатов наблюдений. М.: МИСиС, 2002, 29 с.

. Супрун И.Т., Абрамова С.С. Физика. Методические указания по выполнению лабораторных работ, Электросталь: ЭПИ МИСиС, 2004, 54 с.