 |
Главная |
Дивергенция и ротор векторного поля
|
из
5.00
|
Введение
Для описания физических величин удобно использовать понятие поля. Простейшими физическими величинами являются скаляр и вектор. Их обобщением является тензор. Полное определение тензора мы дадим в курсе тензорного анализа, а сейчас под тензором будем понимать физическую величину, которая может быть задана в виде числа (скаляра), вектора, матрицы или более сложного образования.
Определение 1. В пространстве (среде) задано поле тензора 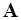 , если этот тензор определен в каждой точке пространства
, если этот тензор определен в каждой точке пространства
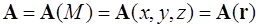 .
.
В качестве 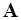 можно выбрать скаляр, вектор или тензор более высокого ранга. Рассмотрим основные свойства поля и его характеристики.
можно выбрать скаляр, вектор или тензор более высокого ранга. Рассмотрим основные свойства поля и его характеристики.
Скалярное поле
Определение 1. Поле 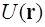 называется скалярным, если в каждой точке пространства определено значение скалярной величины
называется скалярным, если в каждой точке пространства определено значение скалярной величины 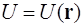 .
.
Поле может зависеть также и от времени
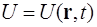 .
.
Здесь t играет роль параметра. Примеры скалярных полей: температура в каждой точке сплошной среды, плотность вещества или электрического заряда (как функция координат точек среды), электрический потенциал,…
Определение 2. Поверхностью уровня скалярного поля 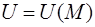 называется совокупность точек удовлетворяющих уравнению
называется совокупность точек удовлетворяющих уравнению
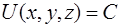 ,
,
где С - некоторая постоянная.
На плоскости уравнение
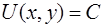
определяет линии уровня.
Выберем в пространстве некоторое направление l, которое задается единичным вектором (ортом) 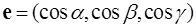 . Рассмотрим две точки М и
. Рассмотрим две точки М и 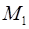 , лежащие на этой линии
, лежащие на этой линии
Определение 3. Производной от функции 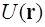 по направлению l называется предел
по направлению l называется предел
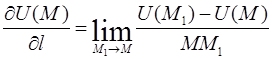 .
.
Эта величина характеризует быстроту изменения функции 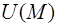 в направлении
в направлении 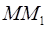 . Имеем
. Имеем
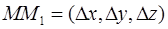 ,
,
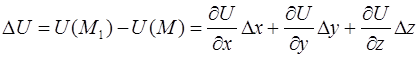 ,
,
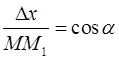 ,
, 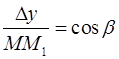 ,
, 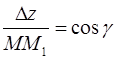 .
.
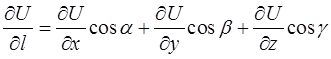
Если направление задается вектором 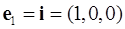 , то
, то
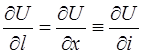 .
.
Аналогично, для 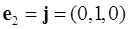
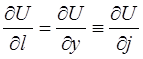
и для 
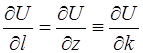 .
.
Определение 4. Градиентом скалярной функции 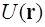 называется вектор
называется вектор
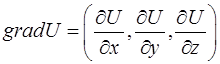 .
.
В математике часто используется символ (читается «набла»)
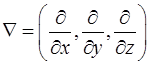 ,
,
который называют оператором дифференцирования или оператором Гамильтона. С помощью этого оператора градиент функции может быть записан в виде
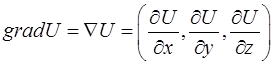 .
.
Теорема 1. Производная скалярного поля 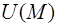 в точке М в направлении орта
в точке М в направлении орта 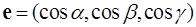 равна проекции градиента поля
равна проекции градиента поля 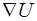 на направление орта
на направление орта 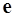 .
.
Доказательство. Производную по направлению, определяемому ортом 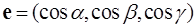 , можно записать в виде скалярного произведения
, можно записать в виде скалярного произведения
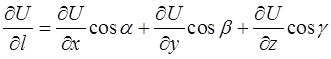
С другой стороны
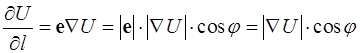
где φ - угол между векторами е и 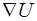 .
.
Максимальное значение 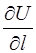 достигается при
достигается при 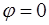 , когда
, когда 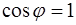 . Следовательно, градиент функции
. Следовательно, градиент функции 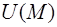 указывает направление максимального возрастания этой функции.
указывает направление максимального возрастания этой функции.
Векторное поле
Определение 1. Поле 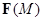 называется векторным, если в каждой точке пространства определено значение векторной величины
называется векторным, если в каждой точке пространства определено значение векторной величины 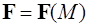 .
.
Примеры векторных полей: напряженность электрического поля, поле скоростей в движущейся среде, напряженность магнитного поля,…
Определение 2. Векторными линиями поля 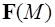 называются кривые, касательные в каждой точке которых совпадают с направлениями вектора
называются кривые, касательные в каждой точке которых совпадают с направлениями вектора 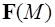 в этой точке. На рисунке показано поле скоростей
в этой точке. На рисунке показано поле скоростей 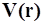 движущейся жидкости.
движущейся жидкости.
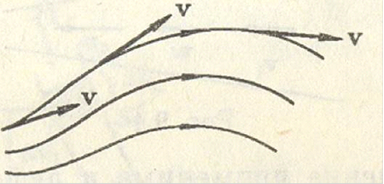
В электростатике векторные линии называют силовыми линиями или линиями напряженности электрического поля.
Теорема 1. Если задано векторное поле 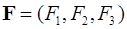 , то векторные линии этого поля описываются системой дифференциальных уравнений
, то векторные линии этого поля описываются системой дифференциальных уравнений
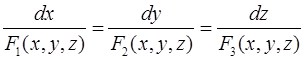 .
.
Доказательство. На рисунке в точке М показаны элемент длины векторной линии 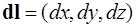 и вектор поля
и вектор поля  .
.
Запишем условие параллельности двух векторов:
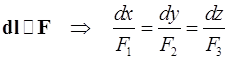 .
.
Если векторное поле определяет скорость движения среды 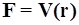 , то векторные линии называются линиями тока.
, то векторные линии называются линиями тока.
Пример 1. Найти векторную линию векторного поля 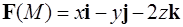 , проходящую через точку
, проходящую через точку 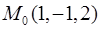 .
.
Решение. Имеем систему дифференциальных уравнений
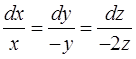
с начальными условиями
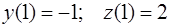 .
.
Проинтегрируем систему:
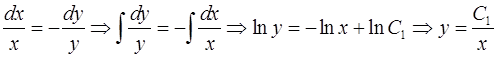 ,
,
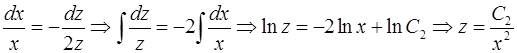 .
.
Используем начальные условия:
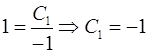 ;
; 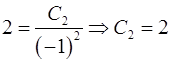 .
.
Ответ: 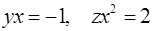 .
.
Пример 2. Найти линии тока плоского потока жидкости, характеризуемого вектором скорости 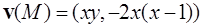 .
.
Ответ: 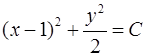 .
.
Дивергенция и ротор векторного поля
Важнейшими характеристиками векторного поля являются ротор и дивергенция. В этом параграфе мы рассмотрим математическое описание этих характеристик векторных поле и методы их вычисления с помощью дифференциальных операций. При этом мы будем использовать только декартову систему координат. Более полное определение дивергенции и ротора и их физический смысл рассмотрим в следующей главе. Вычисление этих величин в криволинейных системах координат рассмотрим позже.
Рассмотрим векторное поле 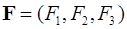 , заданное в трехмерном пространстве.
, заданное в трехмерном пространстве.
Определение 1. Дивергенцией векторного поля 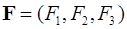 называется число, которое определяется выражением
называется число, которое определяется выражением
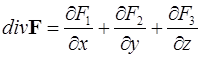 .
.
При этом предполагается, что соответствующие частные производные существуют в рассматриваемой точке. Дивергенцию векторного поля, так же, как и градиент, можно записать, используя оператор набла
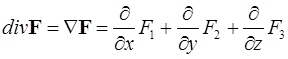 .
.
Здесь дивергенция представлена как скалярное произведение векторов  и F. Отметим без доказательства, что дивергенция описывает плотность источников, создающих поле
и F. Отметим без доказательства, что дивергенция описывает плотность источников, создающих поле 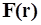 .
.
Пример 1. Вычислить дивергенцию векторного поля 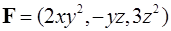 в точке
в точке 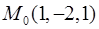 .
.
Ответ:
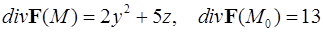 .
.
Определение 2. Ротором векторного поля 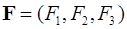 называется вектор, который определяется выражением
называется вектор, который определяется выражением
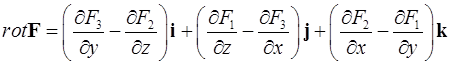 .
.
Отметим, что в представленной сумме индексы в соседних слагаемых изменяются согласно правилу круговой перестановки с учетом правила 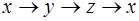 .
.
Ротор векторного поля 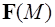 можно записать с помощью оператора набла
можно записать с помощью оператора набла
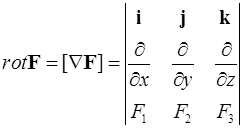 .
.
Ротор характеризует тенденцию к вращению или завихрению векторного поля 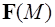 , поэтому иногда его называют вихрем и обозначают curlF.
, поэтому иногда его называют вихрем и обозначают curlF.
Пример 1. Вычислить ротор векторного поля 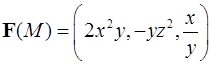 в точке
в точке 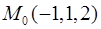 .
.
Ответ: 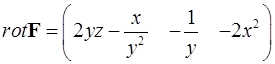 ,
,
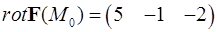 .
.
Иногда возникает необходимость вычисления градиента векторного поля 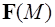 . В этом случае вычисляется градиент от каждой компоненты векторного поля. В результате получается тензор второго ранга, которым и определяется градиент вектора. Этот тензор можно описать матрицей
. В этом случае вычисляется градиент от каждой компоненты векторного поля. В результате получается тензор второго ранга, которым и определяется градиент вектора. Этот тензор можно описать матрицей
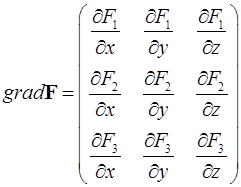 .
.
Для описания таких объектов удобно использовать тензорные обозначения
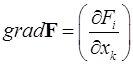 ,
,
полагая 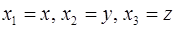 . Использование тензорных методов упрощает математические операции над такими объектами. Детальное изложение аппарата тензорного исчисления дается в курсе «Основы тензорного анализа», который читается параллельно курсу «Дополнительные главы высшей математики».
. Использование тензорных методов упрощает математические операции над такими объектами. Детальное изложение аппарата тензорного исчисления дается в курсе «Основы тензорного анализа», который читается параллельно курсу «Дополнительные главы высшей математики».
Пример 1. Вычислить градиент векторного поля 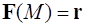 .
.
Решение. Для вычислений используем тензорные обозначения. Имеем
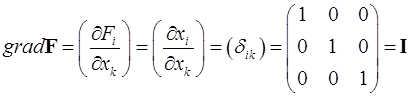 .
.
Здесь 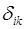 символ Кронекера,
символ Кронекера,  - единичная матрица.
- единичная матрица.
Ответ: 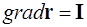 .
.
Пример 2. Вычислить градиент скалярного поля 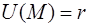 и сравнить выражения
и сравнить выражения 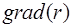 и
и 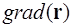 .
.
|
из
5.00
|
Обсуждение в статье: Дивергенция и ротор векторного поля |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

