 |
Главная |
Глава 1. Интегральное исчисление (продолжение 1 семестра).
|
из
5.00
|
Томский государственный университет систем управления и радиоэлектроники
Приходовский М.А.
Математика - 2 семестр
Курс лекций
Учебное пособие
Для специальностей
Информатика и вычислительная техника»
Инфокоммуникационные технологии и системы связи»
Радиоэлектронные системы и комплексы»
Томск
ТУСУР
2020
Настоящее электронное учебное пособие составлено по материалам лекций в группах 589-1,2,3, 129, 1В9 весной 2020 года.
Оглавление по темам
| Глава 1. Интегральное исчисление ................................................................ § 1 Несобственные интегралы............................................................................ § 2 Кратные интегралы...................................................................................... | 5 5 13 |
Оглавление по номерам лекций
| Лекция № 1. 04.02.2020........................................................ Лекция № 2. 11.02.2020........................................................ Лекция № 3. 12.02.2020........................................................ | 5 13 |
ЛЕКЦИЯ № 1. 04.02.2020
Глава 1. Интегральное исчисление (продолжение 1 семестра).
§1. Несобственные интегралы.
Возможен случай, когда криволинейная трапеция не ограничена, то есть не может быть вписана в круг некоторого конечного радиуса, а бесконечно вытянута вправо или вверх. Но при этом может быть конечная площадь. Начнём с некоторых примеров:
Пример. Вычислить  .
.
Решение. Такой интеграл можно рассматривать как предел интегралов вида  при
при  . Если вычислить
. Если вычислить  то получится
то получится 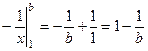 . Предел
. Предел  .
.
Несмотря на неграниченность трапеции под интегралом, площадь конечна. Здесь область определения D(f) не является ограниченной. Тем не менее, трапеция слишком узкая, т.е. её ширина убывает достаточно быстро, чтобы площадь не превысила некоторое число. Так может быть, к примеру, если площади криволинейных трапеций между соседними целыми абсциссами убывают со скоростью сходящейся геометрической прогрессии.

Но есть также примеры, в которых предел бесконечен:
Пример  =
= 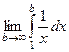 =
=  =
=  =
=  =
=  .
.
Определение. Если функция 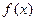 определена и непрерывна на
определена и непрерывна на  , то предел
, то предел 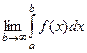 называется несобственным интегралом 1-го рода от функции
называется несобственным интегралом 1-го рода от функции 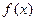 , и обозначается
, и обозначается  .
.
Если предел существует и является конечным числом, то несобственный интеграл называется сходящимся, если предел не существует или равен бесконечности, то интеграл называется расходящимся.
Интеграл  сходящийся, а
сходящийся, а  расходящийся.
расходящийся.
Пример.  =
=  = 1.
= 1.
Область значений E(f) не является ограниченной. При вычислении мы даже и не заметили, что функция неограниченная в окрестности точки 0, т.е.  . Так как первообразная ограниченная, и в неё можно просто подставить
. Так как первообразная ограниченная, и в неё можно просто подставить  и
и  . Вот график этой функции:
. Вот график этой функции:

 можно рассматривать как предел
можно рассматривать как предел 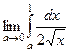 .
.
Определение. Если функция 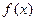 определена и непрерывна на
определена и непрерывна на  и при этом предел
и при этом предел  , то
, то  называется несобственным интегралом 2-го рода от функции
называется несобственным интегралом 2-го рода от функции 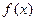 , и обозначается
, и обозначается  .
.
Если функция 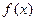 определена и непрерывна на
определена и непрерывна на  и при этом предел
и при этом предел 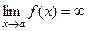 , то
, то  называется несобственным интегралом 2-го рода от функции
называется несобственным интегралом 2-го рода от функции 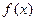 .
.
Итак, если неограниченная D(f), то интеграл называется несобственным интегралом 1-го рода, а если E(f) то несобственным интегралом 2-го рода.
Кстати, для сравнения, геометрическая прогрессия также бывает сходящейся либо расходящейся. Если площадь такой бесконечно вытянутой криволинейной трапеции разбить на части по целым числам, например от 1 до 2, от 2 до 3 и так далее, то если они образуют сходящуюся прогрессию, и в сумме равны некоторой константе, то интеграл сходится.
Есть примеры расходящихся несобственных интегралов.
Пример.  =
=  =
=  . Здесь расходимость из-за неограниченности первообразной.
. Здесь расходимость из-за неограниченности первообразной.
Пример.  =
=  =
=  =
=  =
=  . Но этот предел не существует, синус колеблется от -1 до 1 и при увеличении переменной его график не стремится ни к какой конкретной высоте. И хотя даже функция ограничена, несобственный интеграл расходится. Площадь криволинейной трапеции, при увеличении
. Но этот предел не существует, синус колеблется от -1 до 1 и при увеличении переменной его график не стремится ни к какой конкретной высоте. И хотя даже функция ограничена, несобственный интеграл расходится. Площадь криволинейной трапеции, при увеличении  , то растёт, то снова убывает.
, то растёт, то снова убывает.
Примеры сходящихся несобственных интегралов.
Пример.  =
=  =
=  .
.
Пример.  =
=  =
=  =
=  .
.
Пример.  =
=  =
=  .
.
Теорема 1. Несобственный интеграл сходится  первообразная на границах интегрирования имеет конечный предел.
первообразная на границах интегрирования имеет конечный предел.
Идея доказательства. Действительно,  =
=  =
=  . Второе слагаемое конечное число. Первое слагаемое (предел) есть конечное число тогда и только тогда, когда разность - конечное число. То есть, сходятся именно те несобственные интегралы, где график первообразной стабилизируется по высоте, т.е. имеет конечный предел
. Второе слагаемое конечное число. Первое слагаемое (предел) есть конечное число тогда и только тогда, когда разность - конечное число. То есть, сходятся именно те несобственные интегралы, где график первообразной стабилизируется по высоте, т.е. имеет конечный предел  . Если интеграл 1 рода, то
. Если интеграл 1 рода, то  равносильно сходимости.
равносильно сходимости.
Следствие (необходимый признак сходимости).
 сходится
сходится 
 .
.
Действительно, если  то
то  =
=  =
= 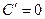 .
.
Замечание. Это необходимый, а не достаточный признак, то есть, из сходимости следует, что f стремится к 0, но не наоборот. При  могут быть как сходящиеся, так и расходящиеся интегралы, а вот если
могут быть как сходящиеся, так и расходящиеся интегралы, а вот если  , тогда только расходящиеся.
, тогда только расходящиеся.
Так, для  и
и  в обоих случаях
в обоих случаях  выполнено. А тем не менее, первых из них расходится, а второй сходится.
выполнено. А тем не менее, первых из них расходится, а второй сходится.
Как мы увидели, овольно нередкой является ситуация, когда производная стремится к бесконечности, а сама функция (то есть её первообразная) в той же точке является конечной. Геометрическая интерпретация. Рассмотрим верхнюю полуокружность. При приближении к точке (1,0) касательная стремится к вертикальному положению, тангенс угла её наклона к  . А при этом сама полуокружность
. А при этом сама полуокружность  ограничена по высоте:
ограничена по высоте:

Теорема 2.
1) Несобственный интеграл 1-го рода  сходится
сходится 
 ,
,
2) Несобственный интеграл 2-го рода  сходится
сходится 
 .
.
Доказательство. Сначала рассмотрим первообразную.
 =
=  =
=  , что можно записать в виде
, что можно записать в виде  .
.
Если пределы интегрирования от 1 до  , то не бесконечный результат получится лишь в том случае, когда переменная в знаменателе, то есть степень
, то не бесконечный результат получится лишь в том случае, когда переменная в знаменателе, то есть степень  , то есть
, то есть  , то есть
, то есть  .
.
А если пределы интегрирования от 0 до 1, то наоборот, наличие переменной в знаменателе приводит к тому, сто предел бесконечен, интеграл расходится. То есть для сходимости, надо чтобы степень была такая, чтобы переменная находилась именно в числителе. Тогда 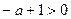 , то есть,
, то есть,  ,
,  . Что и требовалось доказать.
. Что и требовалось доказать.
Обратите внимание, что в случае  расходятся оба этих интеграла, так как первообразная -это логарифм, а он не ограничен ни при
расходятся оба этих интеграла, так как первообразная -это логарифм, а он не ограничен ни при  , ни при
, ни при 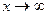 .
.
Для таких интегралов 2 рода, для сходимости надо, чтобы степень перешла в положительные, например, если у функции степень  , а у первообразной на 1 больше, уже
, а у первообразной на 1 больше, уже  . Если же она
. Если же она  , то после интегрирования станет
, то после интегрирования станет  , то есть ещё не переходит через 0 в положительные.
, то есть ещё не переходит через 0 в положительные.
Примеры
| 1 рода | 
| 
| 
| 
| 
| 
|
| 2 рода | 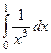
| 
| 
| 
| 
| 
|

| 3 | 2 | 1,5 | 1 | 1/2 | 1/3 |
Жёлтым цветом здесь выделены сходящиеся интегралы.
Теорема 3. Признак сравнения в конечной (непредельной) форме.
Если для неотрицательных функций  верно
верно 
то: если сходится  , то сходится
, то сходится  .
.
Действительно, если интеграл для большей функции равен C, то для меньшей он меньше чем C, то есть, не равен бесконечности.
Пример. Выяснить сходимость интеграла  .
.
Учитывая тот факт, что при  верно
верно  , получается
, получается

 . Тогда
. Тогда  <
<  , а он сходится, так как степень знаменателя больше 1. Тогда и исходный интеграл сходится.
, а он сходится, так как степень знаменателя больше 1. Тогда и исходный интеграл сходится.
Замечание. Аналогично тому, как мы ограничиваем сверху какой-либо сходящейся функцией, можно ограничить снизу какой-либо расходящейся функцией. Если интеграл от этой меньшей функции расходится, то и исходный тоже расходится.
Теорема 4. Признак сравнения в предельной форме.
Если  , причём C отлично от 0 и от
, причём C отлично от 0 и от  (то есть
(то есть 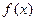 и
и  бесконечно малые одного порядка). Тогда:
бесконечно малые одного порядка). Тогда:
 сходится тогда и только тогда, когда
сходится тогда и только тогда, когда  сходится.
сходится.
Пример на признак в предельной форме.
Выяснить сходимость интеграла  .
.
Рассмотрим для функции 
 более просто устроенную, но эквивалентную ей
более просто устроенную, но эквивалентную ей 
 , котрую можно записать в виде
, котрую можно записать в виде  .
.
Предел их отношения равен 1:
 =
=  =
= 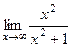 = 1.
= 1.
Тогда сходимость первого интеграла равносильна сходимости второго, то есть можно рассматривать  . Степень
. Степень  , поэтому интеграл сходится.
, поэтому интеграл сходится.
Эти признаки позволяют сравнивать интегралы, содержащие громоздкие функции, с какими-то более простыми «эталонными», например, степенными.
|
из
5.00
|
Обсуждение в статье: Глава 1. Интегральное исчисление (продолжение 1 семестра). |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

